文章目录
1.快速排序
1.基本思想
- 任取待排序元素序列的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
2.hoare版本

-
选key -- 一般是最左边或者最右边的值
- 左作key,让右边先走
- 右作key,让左边先走
-
为什么左边做key,要让右边先走?
- 要保证相遇位置的值,比key小/就是key
- R先走,R停下,L去遇到R
- 相遇位置就是R停下来的位置,必定比key小
- R先走,R没有找到比key小的值,R去遇到了L
- 相遇位置就是L上一轮停下来的位置,比key小/就是key
- R先走,R停下,L去遇到R
- 要保证相遇位置的值,比key小/就是key
-
left向前找大
-
right向后找小
-
单趟排完以后:
- 左边都比key小
- 右边都比key大
-
实现:
cppvoid QuickSort1(int* a, int begin, int end) { //结束条件 -- 只有一个数 --> begin == end || 区间不存在 --> begin > end if (begin >= end) { return; } if (end - begin > 0) { //hoare版本 int left = begin, right = end; int keyi = left; while (left < right) { //右边先走,找小 while (left < right && a[right] >= a[keyi]) //left < right是为了防止越界 { right--; } //左边再走,找大 while (left < right && a[left] <= a[keyi]) { left++; } //交换 Swap(&a[left], &a[right]); } Swap(&a[keyi], &a[left]); keyi = left; //key已经正确的位置上,左边都比key小,右边都比key大 //递归,分治 -- [begin,keyi - 1] keyi [keyi + 1,end] QuickSort1(a, begin, keyi - 1); QuickSort1(a, keyi + 1, end); } else { //直接插入排序 InsertSort(a + begin, end - begin + 1); } }
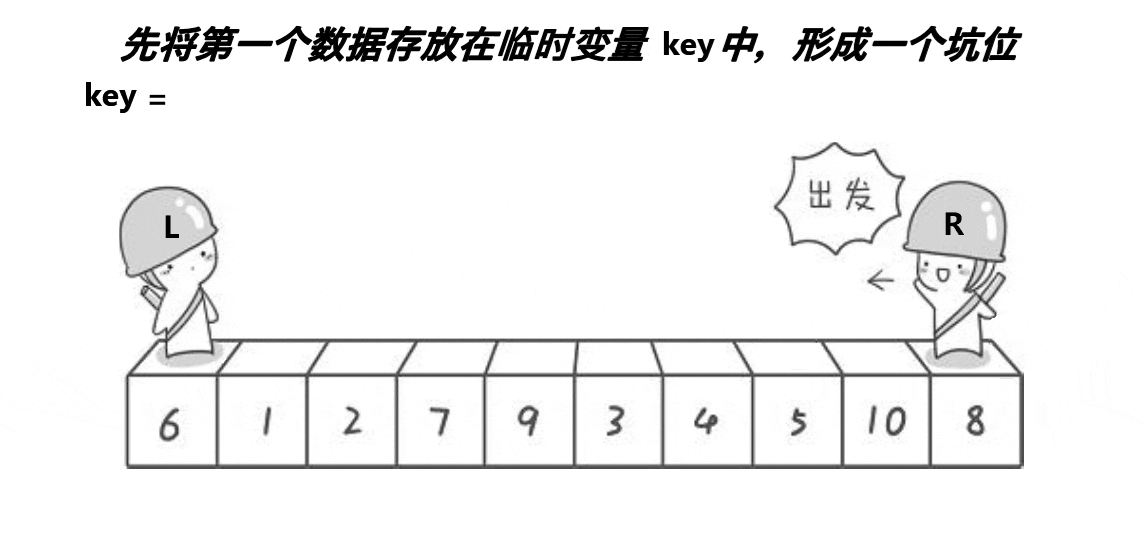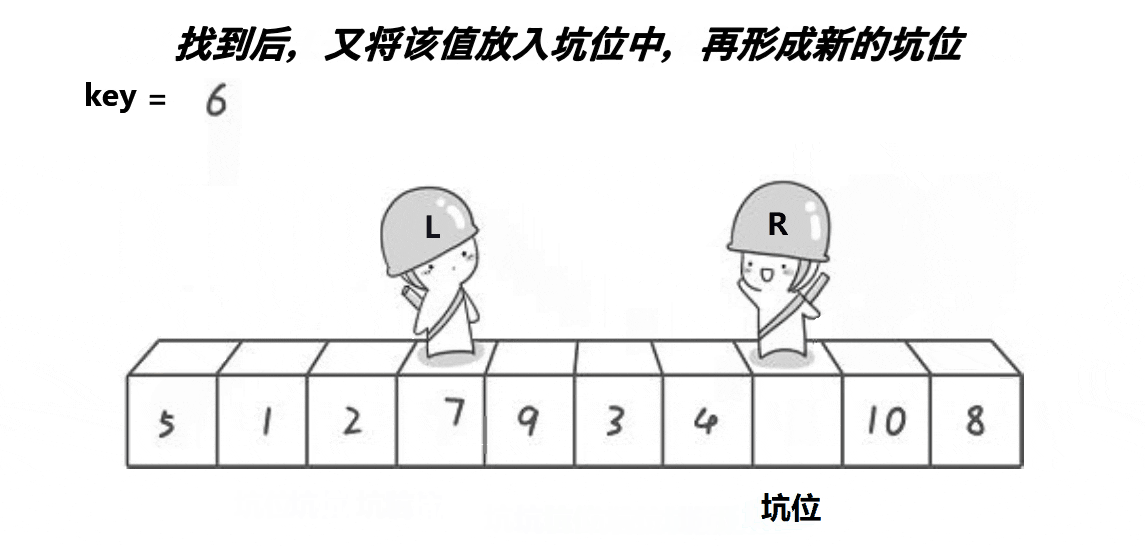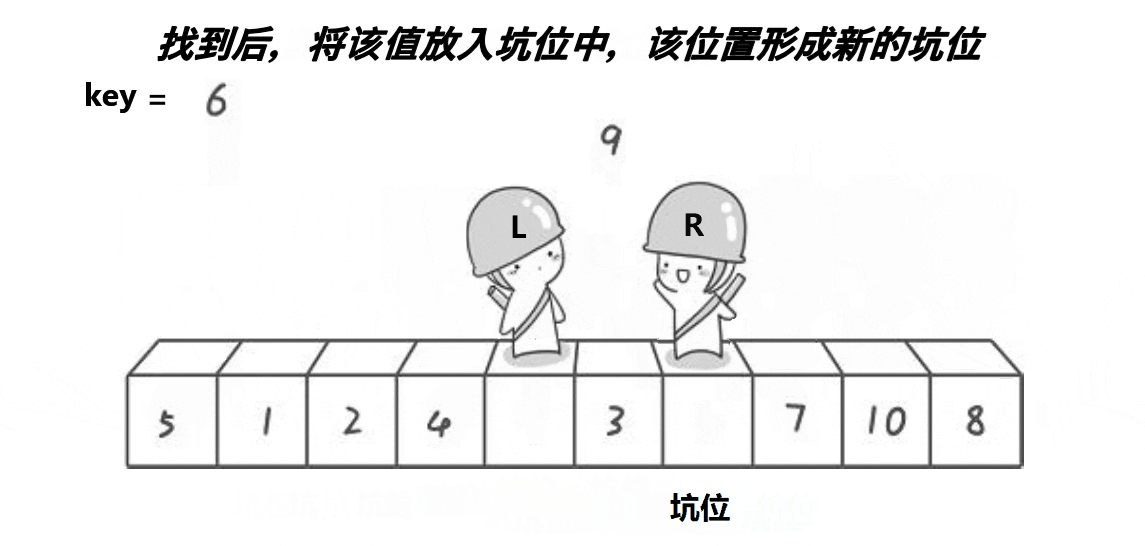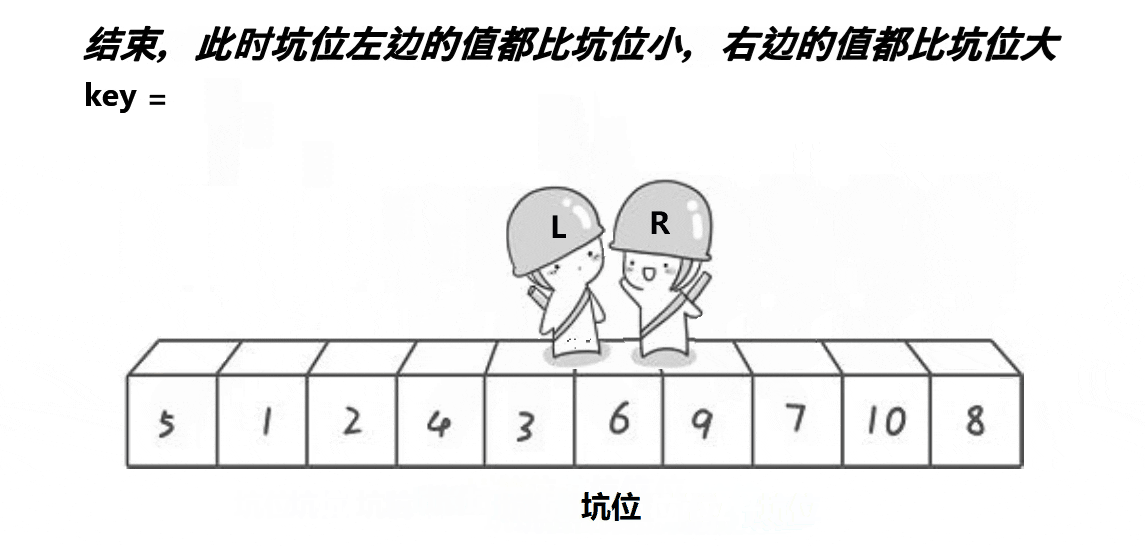
3.挖坑法
-
本质同hoare,但是好理解些
-
右边找小,填到左边的坑里去,这个位置形成新的坑
-
左边找大,填到右边的坑里去,这个位置形成新的坑
-
实现:
cppvoid QuickSort2(int* a, int begin, int end) { //结束条件 -- 只有一个数 --> begin == end || 区间不存在 --> begin > end if (begin >= end) { return; } if (end - begin > 0) { //挖坑法 int key = a[begin]; int piti = begin; int left = begin, right = end; while (begin < end) { //右边找小,填到左边的坑里去,这个位置形成新的坑 while (begin < end && a[right] >= key) { right--; } a[piti] = a[right]; piti = right; //左边找大,填到右边的坑里去,这个位置形成新的坑 while (begin < end && a[left] <= key) { left++; } a[piti] = a[left]; piti = left; } a[piti] = key; //key已经正确的位置上,左边都比key小,右边都比key大 //递归,分治 -- [begin,keyi - 1] keyi [keyi + 1,end] QuickSort2(a, begin, piti - 1); QuickSort2(a, piti + 1, end); } else { //直接插入排序 InsertSort(a + begin, end - begin + 1); } }
4.前后指针版本
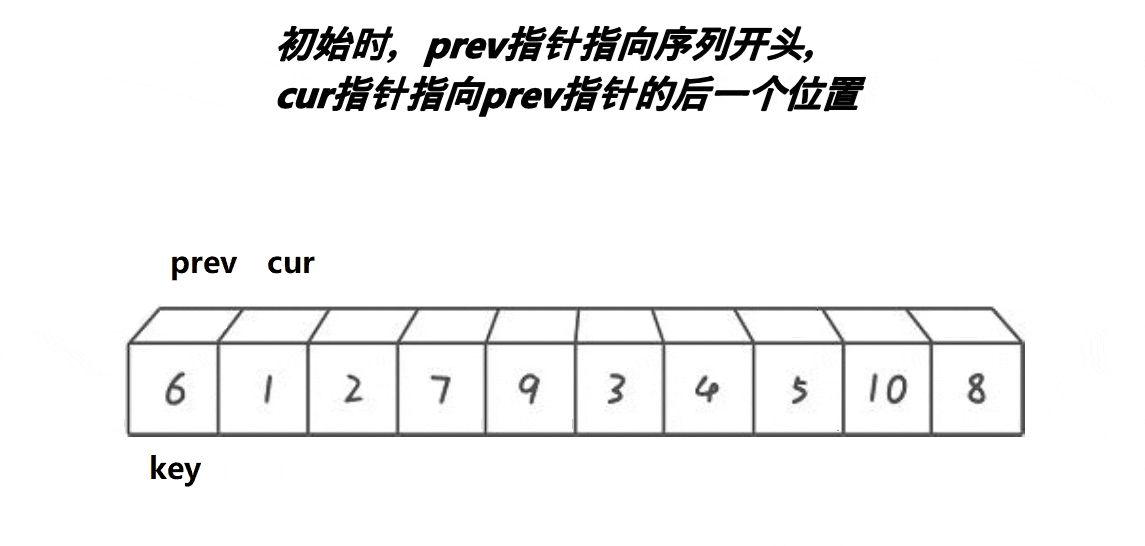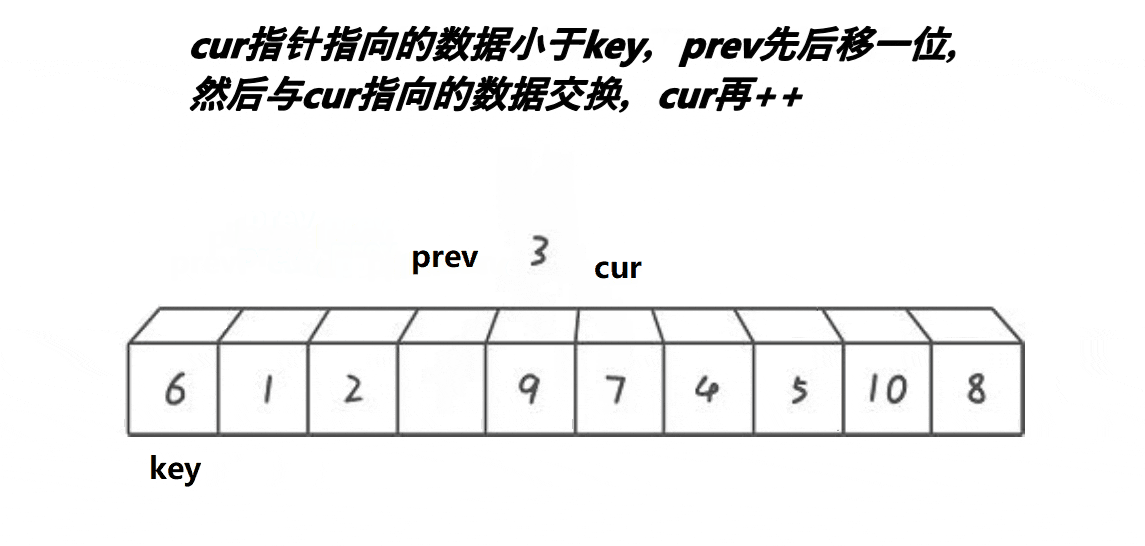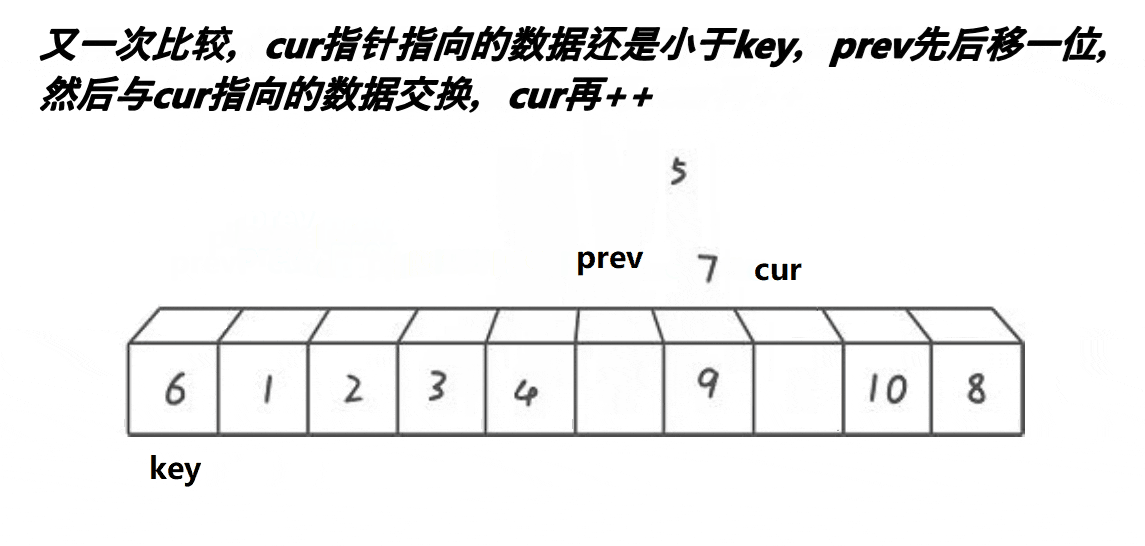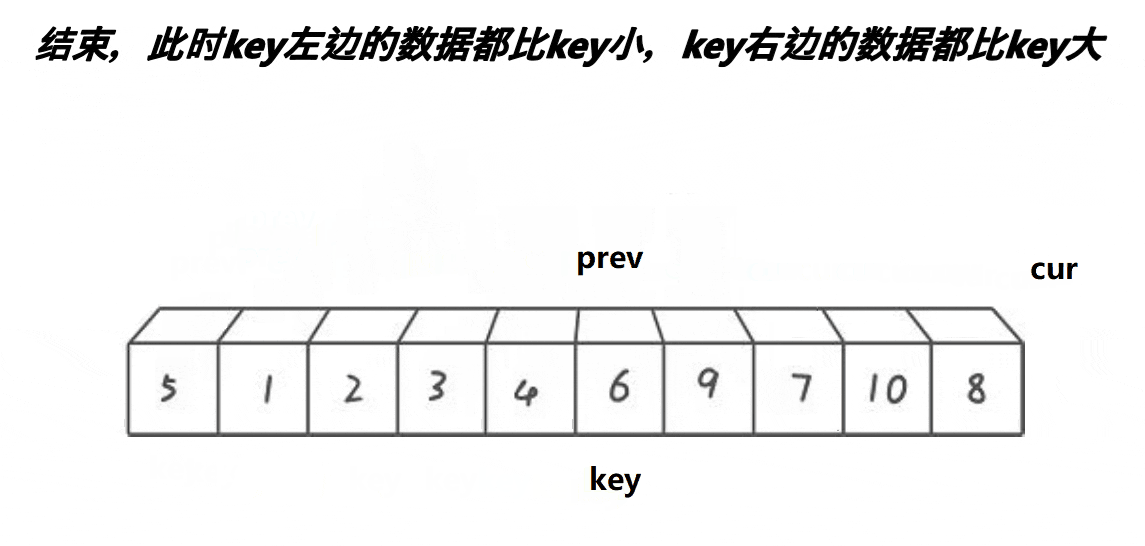
-
cur向前找小,遇到小,则prev++,且交换cur、prev
-
实现:
cppvoid QuickSort3(int* a, int begin, int end) { //结束条件 -- 只有一个数 --> begin == end || 区间不存在 --> begin > end if (begin >= end) { return; } if (end - begin > 0) { //前后指针版本 int prev = begin; int cur = begin + 1; int keyi = begin; //加入三数取中的优化 int midi = GetMidIndex(a, begin, end); Swap(&a[keyi], &a[midi]); while (cur <= end) //一直往后走,遇到小则停下来处理 { //cur找小 if (a[cur] < a[keyi] && ++prev != cur) //防止prev和cur重合时,重复交换 { Swap(&a[prev], &a[cur]); } cur++; } Swap(&a[keyi], &a[prev]); keyi = prev; //key已经正确的位置上,左边都比key小,右边都比key大 //递归,分治 -- [begin,keyi - 1] keyi [keyi + 1,end] QuickSort3(a, begin, keyi - 1); QuickSort3(a, keyi + 1, end); } else { //直接插入排序 InsertSort(a + begin, end - begin + 1); } }
5.非递归版本改写
-
为何需要改写非递归?
- 极端场景下,若深度太深,会出现栈溢出
-
方法:用数据结构栈模拟递归过程
-
实现:
cpp//用栈模拟递归 -- 先进后出 void QuickSortNonR(int* a, int begin, int end) { Stack st; StackInit(&st); StackPush(&st, end); StackPush(&st, begin); while (!isStackEmpty(&st)) { //从栈中取出两个数,作为区间 int left = StackTop(&st); StackPop(&st); int right = StackTop(&st); StackPop(&st); //排序,取keyi int keyi = PartSort3(a, left, right); //此时分成了两个区间 [left, keyi-1] keyi [keyi+1, right] //继续压栈 if (keyi + 1 < right) { StackPush(&st, right); StackPush(&st, keyi + 1); } if (left < keyi - 1) { StackPush(&st, keyi - 1); StackPush(&st, left); } } StackDestroy(&st); } -
特性总结:
- 综合性能&使用场景比较好
- 时间复杂度:O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:不稳定
-
快速排序\]优化方案 * 三数取中法选key * 防止key都是极端数字 --\> 递归过深 --\> 栈溢出 * 递归到小的子区间时,考虑使用插入排序 * 大幅减少递归次数,提高效率 * 例:最后一层递归占了总递归次数的50%,但可能只有极少量的数
2.归并排序
-
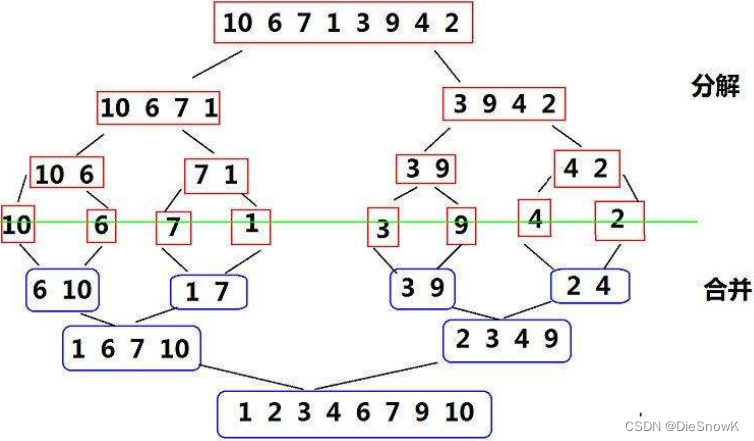
基本思想:
-
分治思维
- 将已有序的子序列合并,得到完全有序的序列
- 即先使每个子序列有序,再使子序列段间有序。
- 若将两个有序表合并成一个有序表,称为二路归并
-
归并排序核心步骤:
-
实现:
cpp//函数名前加_表示这个函数是内部函数,不对外提供接口 - 子函数 //后序思想 void _MergeSort(int* a, int begin, int end, int* tmp) { if (begin >= end) { return; } int mid = (begin + end) / 2; //[begin, mid] [mid+1, end] 分治递归,让子区间有序 _MergeSort(a,begin,mid,tmp); _MergeSort(a,mid+1,end,tmp); //归并 [begin, mid] [mid+1, end] int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int i = begin1; while (begin1 <= end1 && begin2 <= end2) //有一组结束则结束 { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } //已经有一组结束了,拷贝另一组剩余的 while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } //把归并数据拷贝回原数组 memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int)); } //时间复杂度:O(N*logN) //空间复杂度:O(N) void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("MergeSort"); exit(-1); } _MergeSort(a, 0, n - 1, tmp); free(tmp); } -
非递归版本改写
-
实现:
-
①
cppvoid MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc:"); exit(-1); } //手动归并 int gap = 1; //每次归并的元素个数 while (gap < n) { for (int i = 0; i < n; i += 2 * gap) { //[i, i+gap-1] [i+gap,i+2*gap-1] int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //越界处理 - 修正边界 if (end1 >= n) { end1 = n - 1; //[begin2, end2]修正为不存在区间 begin2 = n; end2 = n - 1; } else if (begin2 >= n) { // [begin2, end2]修正为不存在区间 begin2 = n; end2 = n - 1; } else if (end2 >= n) { end2 = n - 1; } //归并 int j = begin1; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } } //全部归并完后,拷贝回原数组 memcpy(a, tmp, sizeof(int) * n); gap *= 2; } free(tmp); } -
②
cppvoid MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc:"); exit(-1); } //手动归并 int gap = 1; //每次归并的元素个数 while (gap < n) { for (int i = 0; i < n; i += 2 * gap) { //[i, i+gap-1] [i+gap,i+2*gap-1] int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //越界处理 //end1越界或者begin2越界,则可以不归并了 if (end1 >= n || begin2 >= n) { break; } else if (end2 >= n) { end2 = n - 1; } //归并 int m = end2 - begin1 + 1; int j = begin1; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } memcpy(a + i, tmp + i, sizeof(int) * m); } gap *= 2; } free(tmp); } -
特性总结:
- 更多解决在磁盘中的外排序问题
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N) -- 缺点
- 稳定性:稳定