前言
本文参考《2025年数据结构考研复习指导（王道论坛组编）》和相关文章，为考试前复习而写。
目录
[第八章 排序](#第八章 排序)
第一章线性表
1.1顺序表
数据结构：
cpp
#include<iostream>
#define MAXSIZE 20 // 定义最大数组大小
using namespace std;
int partition(int* arr, int low, int high);
// 定义一个顺序表结构体
struct Sqlist{
int *elem; // 指向动态分配的数组
int length; // 记录顺序表中的元素数量
};
// 初始化顺序表
int InitList(Sqlist* L){
L->elem = new int[MAXSIZE]; // 动态分配一个整型数组
if(!L->elem){ // 如果分配失败
return 0; // 返回0表示初始化失败
}
L->length = 0; // 初始化长度为0
return 1; // 返回1表示初始化成功
}
// 在顺序表中的第i个位置插入元素e
int ListInsert(Sqlist* L, int i, int e){
if(L->length == MAXSIZE){ // 如果顺序表已满
return 0; // 返回0表示插入失败
}
if(i < 1 || i > L->length + 1){ // 如果插入位置不合法
return 0; // 返回0表示插入失败
}
if(i <= L->length){ // 如果插入位置在表尾或中间
for(int k = L->length - 1; k >= i - 1; k--){ // 将插入位置及其后的元素后移
L->elem[k + 1] = L->elem[k];
}
}
L->elem[i - 1] = e; // 在第i个位置插入元素e
L->length++; // 表长度加1
return 1; // 返回1表示插入成功
}
// 删除顺序表中的第i个位置的元素，并通过*e返回其值
int ListDelete(Sqlist* L, int i, int *e){
if(L->length == 0){ // 如果顺序表为空
return 0; // 返回0表示删除失败
}
if(i < 1 || i > L->length){ // 如果删除位置不合法
return 0; // 返回0表示删除失败
}
*e = L->elem[i - 1]; // 通过*e返回被删除元素的值
if(i < L->length){ // 如果删除位置不是表尾
for(int k = i; k < L->length; k++){ // 将删除位置后的元素前移
L->elem[k - 1] = L->elem[k];
}
}
L->length--; // 表长度减1
return 1; // 返回1表示删除成功
}
// 获取顺序表中的第i个位置的元素，并通过*e返回其值
int GetElem(Sqlist* L, int i, int *e){
if(L->length == 0 || i < 1 || i > L->length){ // 如果表为空或位置不合法
return 0; // 返回0表示获取失败
}
*e = L->elem[i - 1]; // 通过*e返回第i个位置的元素值
return 1; // 返回1表示获取成功
}
// 输出顺序表中的所有元素
void OutPut(Sqlist* L){
for(int i = 0; i < L->length; i++){ // 遍历顺序表
cout << L->elem[i] << " "; // 输出每个元素
}
}
// 快速排序的辅助函数，用于交换两个元素的值
void swap(int* a, int* b) {
int t = *a;
*a = *b;
*b = t;
}
// 快速排序的核心函数
void quickSort(int* arr, int low, int high) {
if (low < high) {
// partitionIndex 是分区操作后基准元素的正确位置
int partitionIndex = partition(arr, low, high);
// 分别对分区前后的子序列进行快速排序
quickSort(arr, low, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, high);
}
}
// 分区操作，将小于基准元素的移到左边，大于基准元素的移到右边
int partition(int* arr, int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = (low - 1); // 指向比基准小的元素的最后一个位置
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++; // 发现小于基准的元素，i右移
swap(&arr[i], &arr[j]); // 交换元素
}
}
swap(&arr[i + 1], &arr[high]); // 将基准元素放到正确的位置
return (i + 1); // 返回基准元素的索引
}
// 调用快速排序的函数
void quickSort(Sqlist* L) {
quickSort(L->elem, 0, L->length - 1);
}
int main(){
Sqlist L; // 声明一个顺序表
if(InitList(&L)){ // 初始化顺序表
ListInsert(&L, 1, 10); // 在第1个位置插入元素10
}
quickSort(&L);//对顺序表进行快速排序
OutPut(&L); // 输出顺序表中的所有元素
return 0;
}1.2单链表
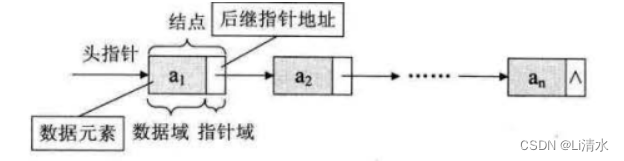
cpp
#include<iostream>
#include<vector>
using namespace std;
// 定义单链表节点结构体
struct ListNode {
int val; // 存储节点的值
ListNode* next; // 指向下一个节点的指针
};
// 创建链表
ListNode* CreateList() {
ListNode* head = new ListNode(); // 创建头节点
head->next = nullptr; // 初始化头节点的next指针为空
return head; // 返回头节点
}
// 在链表中插入元素
void Insert(ListNode* head, int i, int val) {
ListNode* current = head; // 初始化current为头节点
while (i-- > 0) { // 循环i次，找到要插入的位置
current = current->next; // current后移
}
if (current) { // 如果current不为空，表示找到了位置
current->next = new ListNode{val, nullptr}; // 创建新节点并连接到链表
}
}
// 删除链表中的元素
void Delete(ListNode* head, int i) {
ListNode* current = head; // 初始化current为头节点
while (i-- > 0) { // 循环i次，找到要删除的位置
current = current->next; // current后移
}
if (current) { // 如果current不为空，表示找到了位置
current->next = current->next->next; // 跳过要删除的节点
delete current->next; // 释放要删除的节点的内存
}
}
// 获取链表中的元素
int Get(ListNode* head, int i) {
ListNode* current = head->next; // 初始化current为头节点的下一个节点
while (i-- > 0) { // 循环i次，找到要获取的元素
current = current->next; // current后移
}
return current ? current->val : -1; // 返回元素值，如果current为空，返回-1
}
// 输出链表
void Output(ListNode* head) {
ListNode* current = head->next; // 初始化current为头节点的下一个节点
while (current) { // 循环直到current为空
cout << current->val << " "; // 输出当前节点的值
current = current->next; // current后移
}
}
// 快速排序的辅助函数，用于交换两个元素的值
void swap(ListNode* a, ListNode* b) {
int t = a->val; // 存储a节点的值
a->val = b->val; // 将a节点的值替换为b节点的值
b->val = t; // 将b节点的值替换为a节点的值
}
// 快速排序的核心函数
void quickSort(ListNode* head) {
quickSort(head, nullptr, nullptr); // 递归函数，参数low和high分别指向链表的开始和结束
}
// 分区操作，将小于基准元素的移到左边，大于基准元素的移到右边
void quickSort(ListNode* head, ListNode* low, ListNode* high) {
if (low != high) { // 如果low和high不指向同一个节点，说明链表中有多个元素
ListNode* pivot = partition(head, low, high); // 执行分区操作
// 对分区前后的子序列进行快速排序
quickSort(head, low, pivot); // 对分区前的子序列进行排序
quickSort(head, pivot->next, high); // 对分区后的子序列进行排序
}
}
// 分区操作，将小于基准元素的移到左边，大于基准元素的移到右边
ListNode* partition(ListNode* head, ListNode* low, ListNode* high) {
ListNode* pivot = high->next; // 选择最后一个节点作为基准
ListNode* i = low; // 指向比基准小的元素的最后一个位置
while (low != high) { // 当low和high不指向同一个节点时，继续分区
if (low->next->val < pivot->val) { // 如果low->next的值小于基准值
i = low; // i后移到low的位置
swap(i->next, low->next); // 交换low->next和i->next的值
}
low = low->next; // low后移
}
swap(i->next, pivot); // 将基准值放到正确的位置
return i; // 返回基准值的索引
}
int main() {
ListNode* head = CreateList(); // 创建链表
Insert(head, 0, 5); // 在第0个位置插入元素5
Insert(head, 1, 3); // 在第1个位置插入元素3
Insert(head, 2, 7); // 在第2个位置插入元素7
Insert(head, 3, 1); // 在第3个位置插入元素1
cout << "Before sorting:" << endl; // 输出排序前的链表
Output(head);
quickSort(head); // 对链表进行快速排序
cout << "After sorting:" << endl; // 输出排序后的链表
Output(head);
return 0; // 程序结束
}1.3循环链表
1.4双向链表
cpp
#include<iostream>
#include<vector>
using namespace std;
// 定义双向链表节点结构体
struct DoublyListNode {
int val;
DoublyListNode* prev;
DoublyListNode* next;
};
// 创建双向链表
DoublyListNode* CreateDoublyList() {
DoublyListNode* head = new DoublyListNode(); // 创建头节点
head->prev = nullptr;
head->next = nullptr;
return head;
}
// 在双向链表中插入元素
void Insert(DoublyListNode* head, int i, int val) {
DoublyListNode* current = head;
while (i-- > 0) {
current = current->next;
}
if (current) {
current->next = new DoublyListNode{val, current, nullptr};
current->next->prev = current;
}
}
// 删除双向链表中的元素
void Delete(DoublyListNode* head, int i) {
DoublyListNode* current = head;
while (i-- > 0) {
current = current->next;
}
if (current) {
current->prev->next = current->next;
if (current->next) {
current->next->prev = current->prev;
}
delete current;
}
}
// 获取双向链表中的元素
int Get(DoublyListNode* head, int i) {
DoublyListNode* current = head->next;
while (i-- > 0) {
current = current->next;
}
return current ? current->val : -1;
}
// 输出双向链表
void Output(DoublyListNode* head) {
DoublyListNode* current = head->next;
while (current) {
cout << current->val << " ";
current = current->next;
}
}
// 快速排序的辅助函数，用于交换两个元素的值
void swap(DoublyListNode* a, DoublyListNode* b) {
int t = a->val;
a->val = b->val;
b->val = t;
}
// 快速排序的核心函数
void quickSort(DoublyListNode* head) {
quickSort(head, nullptr, nullptr);
}
// 分区操作，将小于基准元素的移到左边，大于基准元素的移到右边
void quickSort(DoublyListNode* head, DoublyListNode* low, DoublyListNode* high) {
if (low != high) {
DoublyListNode* pivot = partition(head, low, high);
// 分别对分区前后的子序列进行快速排序
quickSort(head, low, pivot);
quickSort(head, pivot->next, high);
}
}
// 分区操作，将小于基准元素的移到左边，大于基准元素的移到右边
DoublyListNode* partition(DoublyListNode* head, DoublyListNode* low, DoublyListNode* high) {
DoublyListNode* pivot = high->next; // 选择最后一个节点作为基准
DoublyListNode* i = low; // 指向比基准小的元素的最后一个位置
while (low != high) { // 当low和high不指向同一个节点时，继续分区
if (low->next->val < pivot->val) { // 如果low->next的值小于基准值
i = low; // i后移到low的位置
swap(i->next, low->next); // 交换low->next和i->next的值
}
low = low->next; // low后移
}
swap(i->next, pivot); // 将基准值放到正确的位置
return i; // 返回基准值的索引
}
int main() {
DoublyListNode* head = CreateDoublyList(); // 创建双向链表
Insert(head, 0, 5); // 在第0个位置插入元素5
Insert(head, 1, 3); // 在第1个位置插入元素3
Insert(head, 2, 7); // 在第2个位置插入元素7
Insert(head, 3, 1); // 在第3个位置插入元素1
cout << "Before sorting:" << endl; // 输出排序前的链表
Output(head);
quickSort(head); // 对链表进行快速排序
cout << "After sorting:" << endl; // 输出排序后的链表
Output(head);
return 0; // 程序结束
}第二章栈和队列
2.1栈
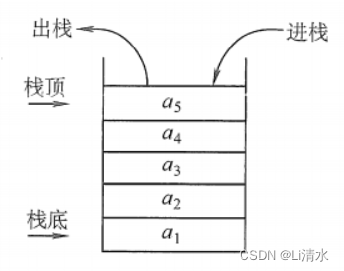
cpp
#include<iostream>
using namespace std;
// 定义顺序栈结构体
struct Stack {
int *elem; // 指向动态分配的数组
int top; // 栈顶指针
int maxSize; // 栈的最大容量
};
// 创建顺序栈
Stack* CreateStack(int maxSize) {
Stack* stack = new Stack();
stack->elem = new int[maxSize];
stack->top = -1; // 初始化栈顶指针为-1
stack->maxSize = maxSize;
return stack;
}
// 入栈操作
void Push(Stack* stack, int val) {
if (stack->top < stack->maxSize - 1) { // 如果栈未满
stack->elem[++stack->top] = val; // 栈顶指针后移，并赋值
} else {
cout << "栈已满，无法入栈。" << endl;
}
}
// 出栈操作
int Pop(Stack* stack) {
if (stack->top >= 0) { // 如果栈非空
return stack->elem[stack->top--]; // 返回栈顶元素，并栈顶指针前移
} else {
cout << "栈为空，无法出栈。" << endl;
return -1; // 返回-1表示栈空
}
}
// 获取栈顶元素
int GetTop(Stack* stack) {
if (stack->top >= 0) { // 如果栈非空
return stack->elem[stack->top]; // 返回栈顶元素
} else {
cout << "栈为空，无法获取栈顶元素。" << endl;
return -1; // 返回-1表示栈空
}
}
// 判断栈是否为空
bool IsEmpty(Stack* stack) {
return stack->top < 0; // 如果栈顶指针小于0，则栈为空
}
// 释放栈内存
void DestroyStack(Stack* stack) {
delete[] stack->elem; // 释放数组内存
delete stack; // 释放栈结构体内存
}
int main() {
Stack* stack = CreateStack(10); // 创建一个最大容量为10的顺序栈
cout << "入栈元素: 10, 20, 30, 40, 50" << endl;
Push(stack, 10);
Push(stack, 20);
Push(stack, 30);
Push(stack, 40);
Push(stack, 50);
cout << "栈顶元素: " << GetTop(stack) << endl;
cout << "出栈元素: " << Pop(stack) << endl;
cout << "栈顶元素: " << GetTop(stack) << endl;
cout << "栈是否为空: " << (IsEmpty(stack) ? "是" : "否") << endl;
DestroyStack(stack); // 释放栈内存
return 0;
}2.2共享栈
cpp
#include<iostream>
#include<mutex>
using namespace std;
// 定义共享栈结构体
struct SharedStack {
int *elem; // 指向动态分配的数组
int top; // 栈顶指针
int maxSize; // 栈的最大容量
mutex mtx; // 互斥锁
};
// 创建共享栈
SharedStack* CreateSharedStack(int maxSize) {
SharedStack* stack = new SharedStack();
stack->elem = new int[maxSize];
stack->top = -1; // 初始化栈顶指针为-1
stack->maxSize = maxSize;
return stack;
}
// 入栈操作
void Push(SharedStack* stack, int val) {
lock_guard<mutex> lock(stack->mtx); // 使用互斥锁保护临界区
if (stack->top < stack->maxSize - 1) { // 如果栈未满
stack->elem[++stack->top] = val; // 栈顶指针后移，并赋值
} else {
cout << "栈已满，无法入栈。" << endl;
}
}
// 出栈操作
int Pop(SharedStack* stack) {
lock_guard<mutex> lock(stack->mtx); // 使用互斥锁保护临界区
if (stack->top >= 0) { // 如果栈非空
return stack->elem[stack->top--]; // 返回栈顶元素，并栈顶指针前移
} else {
cout << "栈为空，无法出栈。" << endl;
return -1; // 返回-1表示栈空
}
}
// 获取栈顶元素
int GetTop(SharedStack* stack) {
lock_guard<mutex> lock(stack->mtx); // 使用互斥锁保护临界区
if (stack->top >= 0) { // 如果栈非空
return stack->elem[stack->top]; // 返回栈顶元素
} else {
cout << "栈为空，无法获取栈顶元素。" << endl;
return -1; // 返回-1表示栈空
}
}
// 判断栈是否为空
bool IsEmpty(SharedStack* stack) {
lock_guard<mutex> lock(stack->mtx); // 使用互斥锁保护临界区
return stack->top < 0; // 如果栈顶指针小于0，则栈为空
}
// 释放栈内存
void DestroySharedStack(SharedStack* stack) {
lock_guard<mutex> lock(stack->mtx); // 使用互斥锁保护临界区
delete[] stack->elem; // 释放数组内存
delete stack; // 释放栈结构体内存
}
int main() {
SharedStack* sharedStack = CreateSharedStack(10); // 创建一个最大容量为10的共享栈
cout << "入栈元素: 10, 20, 30, 40, 50" << endl;
Push(sharedStack, 10);
Push(sharedStack, 20);
Push(sharedStack, 30);
Push(sharedStack, 40);
Push(sharedStack, 50);
cout << "栈顶元素: " << GetTop(sharedStack) << endl;
cout << "出栈元素: " << Pop(sharedStack) << endl;
cout << "栈顶元素: " << GetTop(sharedStack) << endl;
cout << "栈是否为空: " << (IsEmpty(sharedStack) ? "是" : "否") << endl;
DestroySharedStack(sharedStack); // 释放栈内存
return 0;
}2.3链栈
cpp
#include<iostream>
using namespace std;
// 定义链栈节点结构体
struct StackNode {
int val;
StackNode* next;
};
// 创建链栈
StackNode* CreateStack() {
StackNode* head = new StackNode(); // 创建头节点
head->next = nullptr;
return head;
}
// 入栈操作
void Push(StackNode* head, int val) {
StackNode* newNode = new StackNode{val, nullptr}; // 创建新节点
newNode->next = head->next; // 将新节点链接到链表
head->next = newNode; // 头节点指向新节点
}
// 出栈操作
int Pop(StackNode* head) {
if (head->next == nullptr) {
cout << "栈为空，无法出栈。" << endl;
return -1; // 返回-1表示栈空
}
StackNode* temp = head->next; // 临时节点
int val = temp->val; // 保存要返回的值
head->next = temp->next; // 头节点指向下一个节点
delete temp; // 释放临时节点
return val; // 返回栈顶元素
}
// 获取栈顶元素
int GetTop(StackNode* head) {
if (head->next == nullptr) {
cout << "栈为空，无法获取栈顶元素。" << endl;
return -1; // 返回-1表示栈空
}
return head->next->val; // 返回栈顶元素
}
// 判断栈是否为空
bool IsEmpty(StackNode* head) {
return head->next == nullptr; // 如果头节点的next指针为空，则栈为空
}
int main() {
StackNode* stack = CreateStack(); // 创建链栈
cout << "入栈元素: 10, 20, 30, 40, 50" << endl;
Push(stack, 10);
Push(stack, 20);
Push(stack, 30);
Push(stack, 40);
Push(stack, 50);
cout << "栈顶元素: " << GetTop(stack) << endl;
cout << "出栈元素: " << Pop(stack) << endl;
cout << "栈顶元素: " << GetTop(stack) << endl;
cout << "栈是否为空: " << (IsEmpty(stack) ? "是" : "否") << endl;
return 0;
}2.4队列
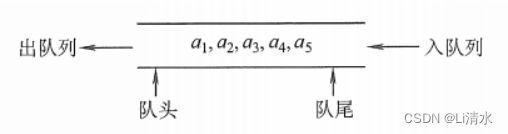
cpp
#include<iostream>
#include<vector>
using namespace std;
// 定义队列结构体
struct Queue {
vector<int> elements; // 使用vector来存储队列元素
};
// 创建队列
Queue* CreateQueue() {
return new Queue(); // 创建队列对象
}
// 入队操作
void Enqueue(Queue* queue, int val) {
queue->elements.push_back(val); // 将元素添加到队列末尾
}
// 出队操作
int Dequeue(Queue* queue) {
if (queue->elements.empty()) { // 如果队列为空
cout << "队列为空，无法出队。" << endl;
return -1; // 返回-1表示队空
}
int val = queue->elements.front(); // 获取队首元素
queue->elements.erase(queue->elements.begin()); // 删除队首元素
return val; // 返回队首元素
}
// 获取队首元素
int GetFront(Queue* queue) {
if (queue->elements.empty()) { // 如果队列为空
cout << "队列为空，无法获取队首元素。" << endl;
return -1; // 返回-1表示队空
}
return queue->elements.front(); // 返回队首元素
}
// 判断队列是否为空
bool IsEmpty(Queue* queue) {
return queue->elements.empty(); // 如果队列大小为0，则队列为空
}
int main() {
Queue* queue = CreateQueue(); // 创建队列
cout << "入队元素: 10, 20, 30, 40, 50" << endl;
Enqueue(queue, 10);
Enqueue(queue, 20);
Enqueue(queue, 30);
Enqueue(queue, 40);
Enqueue(queue, 50);
cout << "队首元素: " << GetFront(queue) << endl;
cout << "出队元素: " << Dequeue(queue) << endl;
cout << "队首元素: " << GetFront(queue) << endl;
cout << "队列是否为空: " << (IsEmpty(queue) ? "是" : "否") << endl;
return 0;
}2.5循环队列
cpp
#include<iostream>
using namespace std;
// 定义循环队列结构体
struct CircularQueue {
int *arr; // 指向动态分配的数组
int front; // 队首指针
int rear; // 队尾指针
int maxSize; // 队列的最大容量
};
// 创建循环队列
CircularQueue* CreateCircularQueue(int maxSize) {
CircularQueue* queue = new CircularQueue();
queue->arr = new int[maxSize];
queue->front = -1; // 初始化队首指针为-1
queue->rear = -1; // 初始化队尾指针为-1
queue->maxSize = maxSize;
return queue;
}
// 入队操作
void Enqueue(CircularQueue* queue, int val) {
if ((queue->rear + 1) % queue->maxSize == queue->front) { // 如果队列已满
cout << "队列已满，无法入队。" << endl;
return;
}
if (queue->front == -1) { // 如果队列为空，队首指针指向0
queue->front = 0;
}
queue->rear = (queue->rear + 1) % queue->maxSize; // 队尾指针后移
queue->arr[queue->rear] = val; // 在队尾插入新元素
}
// 出队操作
int Dequeue(CircularQueue* queue) {
if (queue->front == -1) { // 如果队列为空
cout << "队列为空，无法出队。" << endl;
return -1; // 返回-1表示队空
}
int val = queue->arr[queue->front]; // 获取队首元素
queue->front = (queue->front + 1) % queue->maxSize; // 队首指针后移
return val; // 返回队首元素
}
// 获取队首元素
int GetFront(CircularQueue* queue) {
if (queue->front == -1) { // 如果队列为空
cout << "队列为空，无法获取队首元素。" << endl;
return -1; // 返回-1表示队空
}
return queue->arr[queue->front]; // 返回队首元素
}
// 判断队列是否为空
bool IsEmpty(CircularQueue* queue) {
return queue->front == -1; // 如果队首指针为-1，则队列为空
}
int main() {
CircularQueue* circularQueue = CreateCircularQueue(5); // 创建一个最大容量为5的循环队列
cout << "入队元素: 10, 20, 30, 40, 50" << endl;
Enqueue(circularQueue, 10);
Enqueue(circularQueue, 20);
Enqueue(circularQueue, 30);
Enqueue(circularQueue, 40);
Enqueue(circularQueue, 50);
cout << "队首元素: " << GetFront(circularQueue) << endl;
cout << "出队元素: " << Dequeue(circularQueue) << endl;
cout << "队首元素: " << GetFront(circularQueue) << endl;
cout << "队列是否为空: " << (IsEmpty(circularQueue) ? "是" : "否") << endl;
return 0;
}2.6链队列
cpp
#include<iostream>
using namespace std;
// 定义链队列节点结构体
struct QueueNode {
int val;
QueueNode* next;
};
// 创建链队列
QueueNode* CreateQueue() {
QueueNode* head = new QueueNode(); // 创建头节点
head->next = nullptr;
return head;
}
// 入队操作
void Enqueue(QueueNode* head, int val) {
QueueNode* newNode = new QueueNode{val, nullptr}; // 创建新节点
newNode->next = head->next; // 将新节点链接到链表
head->next = newNode; // 头节点指向新节点
}
// 出队操作
int Dequeue(QueueNode* head) {
if (head->next == nullptr) {
cout << "队列为空，无法出队。" << endl;
return -1; // 返回-1表示队空
}
QueueNode* temp = head->next; // 临时节点
int val = temp->val; // 保存要返回的值
head->next = temp->next; // 头节点指向下一个节点
delete temp; // 释放临时节点
return val; // 返回队首元素
}
// 获取队首元素
int GetFront(QueueNode* head) {
if (head->next == nullptr) {
cout << "队列为空，无法获取队首元素。" << endl;
return -1; // 返回-1表示队空
}
return head->next->val; // 返回队首元素
}
// 判断队列是否为空
bool IsEmpty(QueueNode* head) {
return head->next == nullptr; // 如果头节点的next指针为空，则队列空
}
int main() {
QueueNode* queue = CreateQueue(); // 创建链队列
cout << "入队元素: 10, 20, 30, 40, 50" << endl;
Enqueue(queue, 10);
Enqueue(queue, 20);
Enqueue(queue, 30);
Enqueue(queue, 40);
Enqueue(queue, 50);
cout << "队首元素: " << GetFront(queue) << endl;
cout << "出队元素: " << Dequeue(queue) << endl;
cout << "队首元素: " << GetFront(queue) << endl;
cout << "队列是否为空: " << (IsEmpty(queue) ? "是" : "否") << endl;
return 0;
}2.7双端队列
cpp
#include<iostream>
using namespace std;
// 定义双端队列节点结构体
struct DequeNode {
int val;
DequeNode* next;
DequeNode* prev;
};
// 创建双端队列
DequeNode* CreateDeque() {
DequeNode* head = new DequeNode(); // 创建头节点
DequeNode* tail = new DequeNode(); // 创建尾节点
head->next = tail;
tail->prev = head;
return head;
}
// 入队操作（队尾）
void EnqueueRear(DequeNode* head, int val) {
DequeNode* newNode = new DequeNode{val, nullptr, head->next}; // 创建新节点
head->next->prev = newNode; // 新节点的prev指向当前队尾
head->next = newNode; // 头节点的next指向新节点
}
// 入队操作（队首）
void EnqueueFront(DequeNode* head, int val) {
DequeNode* newNode = new DequeNode{val, head, nullptr}; // 创建新节点
head->prev->next = newNode; // 新节点的next指向当前队首
head->prev = newNode; // 头节点的prev指向新节点
}
// 出队操作（队首）
int DequeueFront(DequeNode* head) {
if (head->next == nullptr) { // 如果队列为空
cout << "队列为空，无法出队。" << endl;
return -1; // 返回-1表示队空
}
DequeNode* temp = head->next; // 临时节点
int val = temp->val; // 保存要返回的值
head->next = temp->next; // 头节点的next指向下一个节点
temp->next->prev = head; // 新节点的prev指向队首
delete temp; // 释放临时节点
return val; // 返回队首元素
}
// 出队操作（队尾）
int DequeueRear(DequeNode* head) {
if (head->next == nullptr) { // 如果队列为空
cout << "队列为空，无法出队。" << endl;
return -1; // 返回-1表示队空
}
DequeNode* temp = head->next; // 临时节点
int val = temp->val; // 保存要返回的值
temp->prev->next = temp->next; // 尾节点的prev指向下一个节点
temp->next->prev = temp->prev; // 新节点的prev指向队尾
delete temp; // 释放临时节点
return val; // 返回队尾元素
}
// 获取队首元素
int GetFront(DequeNode* head) {
if (head->next == nullptr) { // 如果队列为空
cout << "队列为空，无法获取队首元素。" << endl;
return -1; // 返回-1表示队空
}
return head->next->val; // 返回队首元素
}
// 获取队尾元素
int GetRear(DequeNode* head) {
if (head->next == nullptr) { // 如果队列为空
cout << "队列为空，无法获取队尾元素。" << endl;
return -1; // 返回-1表示队空
}
return head->next->val; // 返回队尾元素
}
// 判断队列是否为空
bool IsEmpty(DequeNode* head) {
return head->next == nullptr; // 如果头节点的next指针为空，则队列为空
}
int main() {
DequeNode* deque = CreateDeque(); // 创建双端队列
cout << "入队元素: 10, 20, 30, 40, 50" << endl;
EnqueueFront(deque, 10);
EnqueueFront(deque, 20);
EnqueueRear(deque, 30);
EnqueueRear(deque, 40);
EnqueueFront(deque, 50);
cout << "队首元素: " << GetFront(deque) << endl;
cout << "队尾元素: " << GetRear(deque) << endl;
cout << "出队元素: " << DequeueFront(deque) << endl;
cout << "队首元素: " << GetFront(deque) << endl;
cout << "队列是否为空: " << (IsEmpty(deque) ? "是" : "否") << endl;
return 0;
}第三章串
3.1串
串( string)是由零个或多个字符组成的有限序列，又名叫字符串。
空串：n = 0 n=0n=0时的串称为空串。
空格串：是只包含空格的串。注意它与空串的区别，空格串是有内容有长度的，而且可以不止一个空格。
子串与主串：串中任意个数的连续字符组成的子序列称为该串的子串，相应地，包含子串的串称为主串。
子串在主串中的位置就是子串的第一个字符在主串中的序号。
3.2定长顺序存储
java
#define MAXLEN 255 //预定义最大串长为255
struct sstring{
char ch[MAXLEN]; //每个分量存储一个字符
int length; //串的实际长度
};串的实际长度只能小于等于MAXLEN，超过预定义长度的串值会被舍去，称为截断。
串长有两种表示方法: 一是如上述定义描述的那样，用一个额外的变量len来存放串的长度;二是在串值后面加一一个不计入串长的结束标记字符"\0"
3.3堆分配存储
java
struct HString{
char *ch; //按串长分配存储区，ch指向串的基地址
int length; //串的长度
};3.4串的基本操作
java
StrAssign(&T, chars): 赋值操作。把串T赋值为 chars
Strcopy(&T, S): 复制操作。由串S复制得到串T。
StrEmpty(S): 判空操作。若S为空串,则返回TRUE,否则返回 FALSE
StrCompare(S,T): 比较操作。若S>T,则返回值>0;若S=T,则返回值=0;若S<T,则返回值<0。
StrEngth(S): 求串长。返回串S的元素个数
Substring(&Sub,S,pos,1en):求子串。用Sub返回串S的第pos个字符起长度为len的子串。
Concat(&T,S1,S2): 串联接。用T返回由S1和S2联接而成的新串。
Index(S,T): 定位操作。若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置;否则函数值为0
int Index(Sring S, String T){
int i = 1, n = StrLength(S), m = StrLength(T);
String sub;
while(i <= n-m+1){
SubString(sub, S, i, m); //取主串第i个位置，长度为m的串给sub
if(StrCompare(sub, T) != 0){
++i;
}else{
return i; //返回子串在主串中的位置
}
}
return 0; //S中不存在与T相等的子串
}
Clearstring(&S): 清空操作。将S清为空串
Destroystring(&S): 销毁串。将串S销毁3.5串的模式匹配（BF）
java
int Index(SString S, SString T){
int i = 1, j = 1;
while(i <= S.length && j <= T.length){
if(S.ch[i] == T.ch[j]){
++i; ++j; //继续比较后继字符
}else{
//指针后退重新开始匹配
i = i-j+2;
j = 1;
}
}
if(j > T.length){
return i - T.length;
}else{
return 0;
}
}
3.6kmp
第四章数组
4.1行，列优先存储
1、行优先
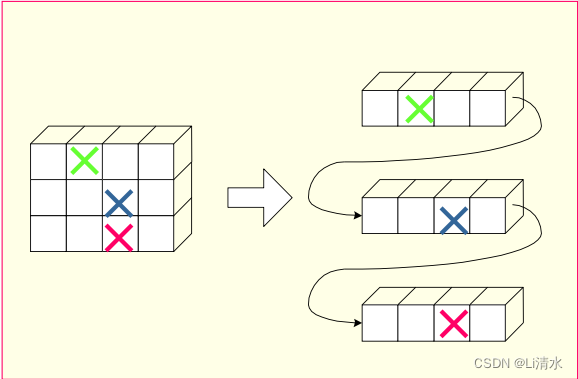
2、列优先
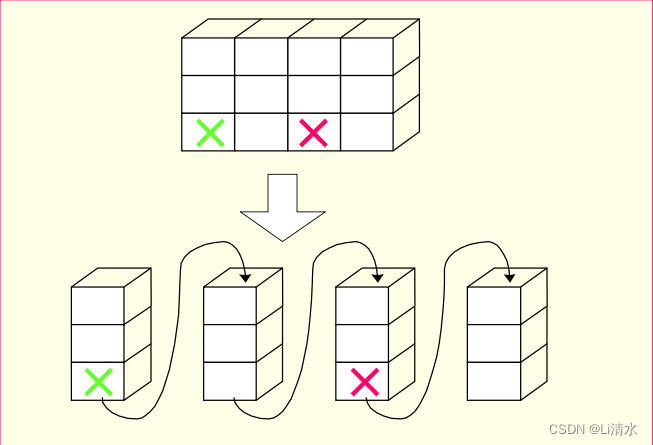
4.2压缩存储
1、对称矩阵
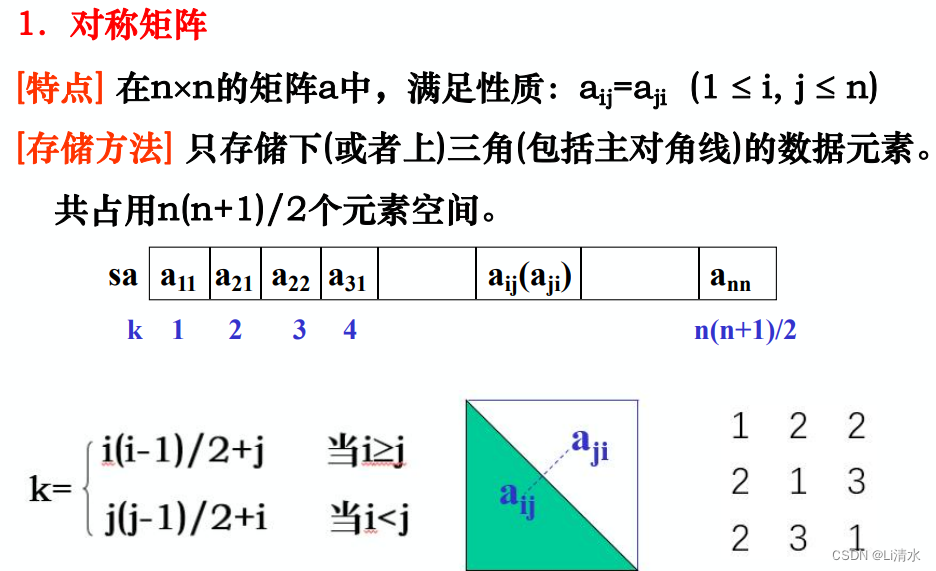2、三角矩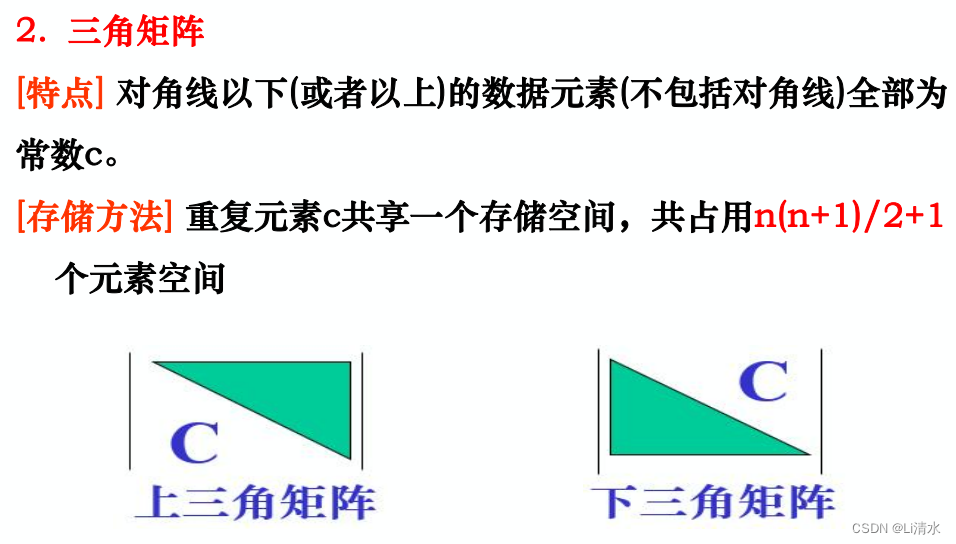阵
3、三对角矩阵 
4、稀疏矩阵
1）三元组
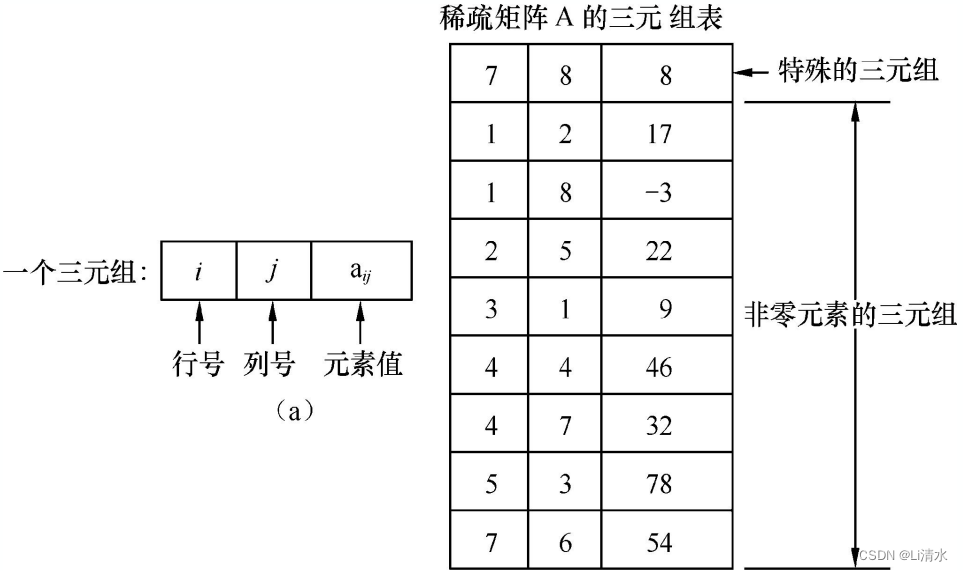
2）带行指针的链表
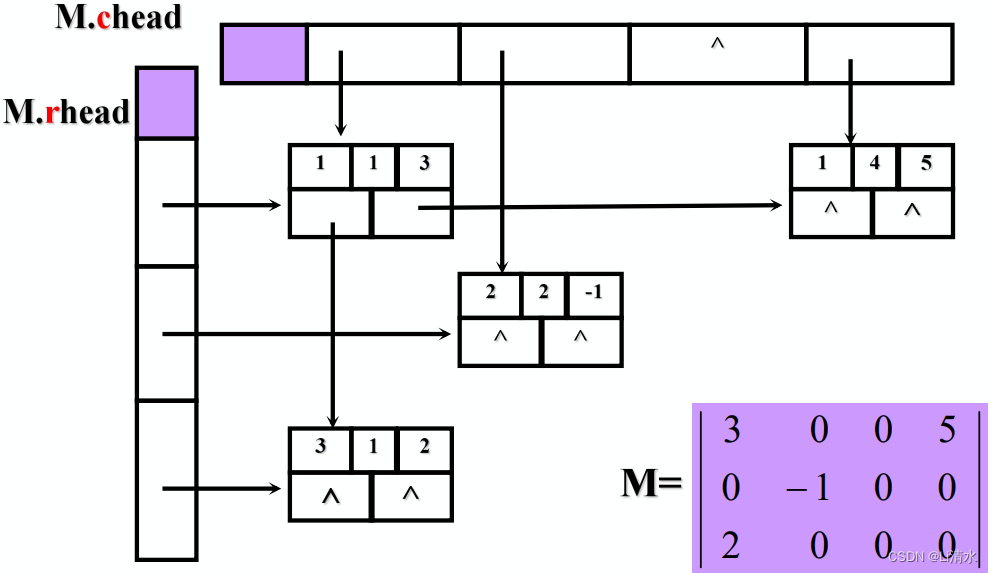
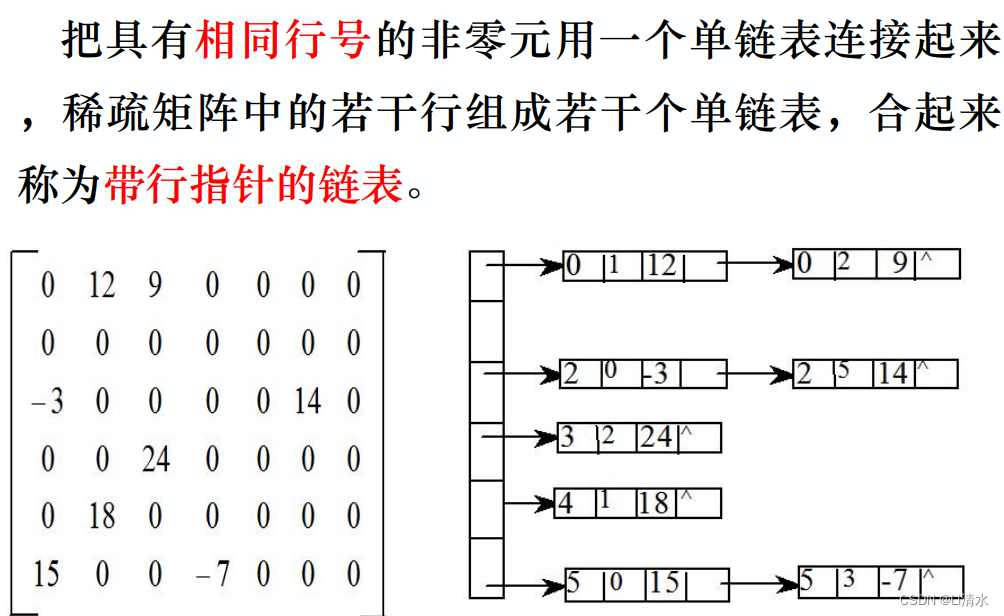3）十字链表
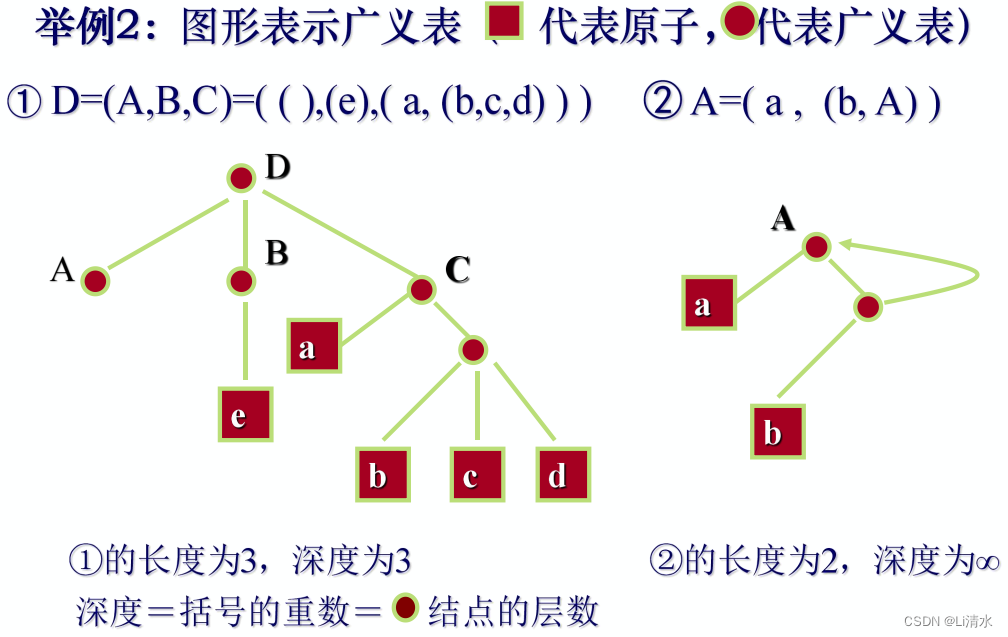
第五章广义表
定义
例题
存储结构
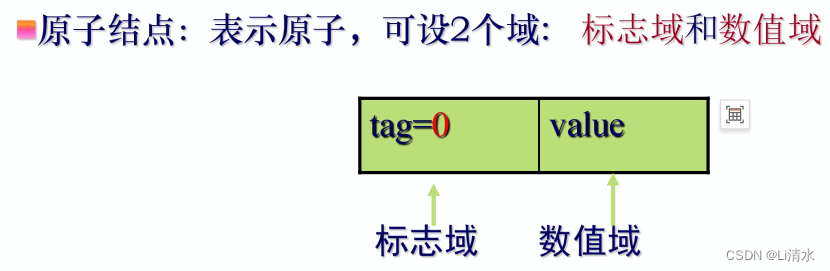原子结点
表结点
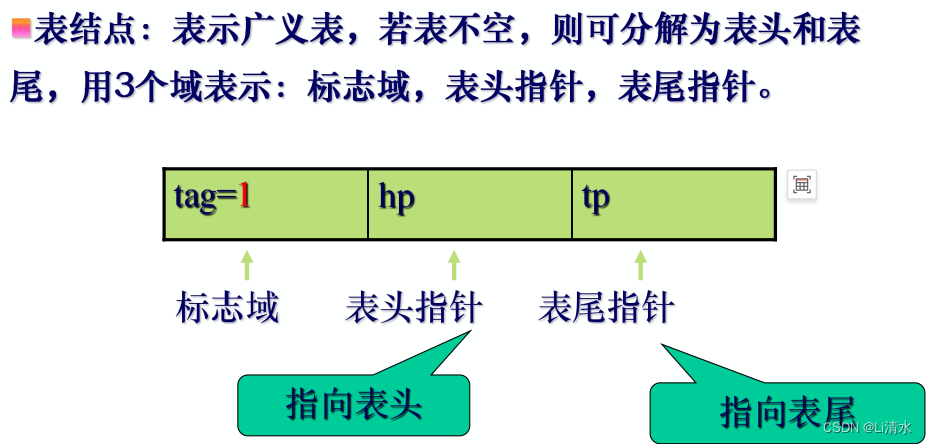
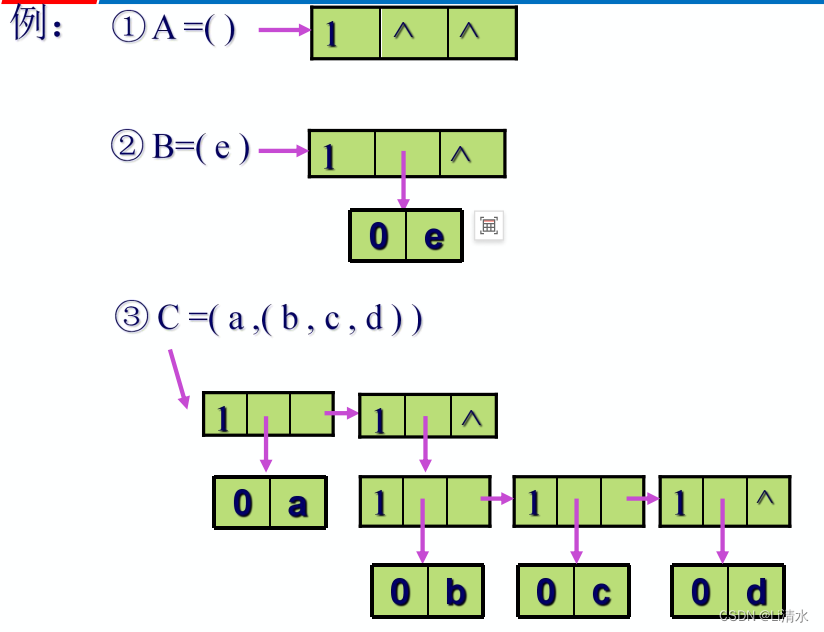
第六章树与二叉树
6.1树
6.1.1基本术语
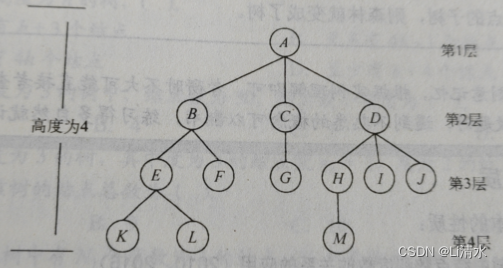
祖先：考虑结点K，从根A到结点K的唯一路径上的所有其他结点，称为结点K的祖先。
子孙：结点B的子孙包括E,F,K,L。
双亲：结点K的双亲为结点E。
孩子：K为E的孩子。
兄弟：有相同双亲的结点为兄弟。K和L为兄弟。
堂兄弟：双亲在同一层的结点互为堂兄弟。K和M互为堂兄弟。
结点的度：树中一个结点的孩子个数。E的度为2.
树的度：树中结点的最大度数。该树的为3.
分支结点：度大于0的结点（非终端结点）。
叶结点：度为0（没有孩子结点）。
结点的深度：结点所在的层次。K为4，E为3.
树的高度：树中的最大层数。
有序树：树中结点的各子树从左到右是有次序的，不能互换，否则称无序树。
6.1.2树的性质
6.2二叉树
6.2.1几种特殊的二叉树
满二叉树：即二叉树中的每层都含有最多的结点。除叶结点之外的每个结点度数均为2。
完全二叉树： 若有度为一的结点，则最多只可能有一个，且该结点只有左孩子而无右孩子。
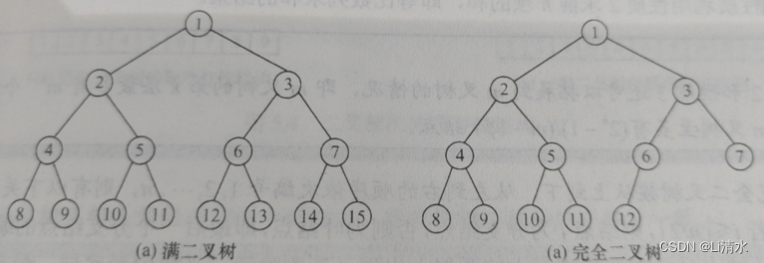
二叉排序树：左子树上所有结点均小于根结点。右子树上所有结点均大于根结点 。左右子树又各是一颗二叉排序树。
平衡二叉树：树中任意一个结点的左子树和右子树的高度之差的绝对值不超过一。
正则二叉树：树中只有度为0或2的结点。
6.2.2二叉树的性质
1、设度为0，1，2的结点个数分别为n0，n1，n2。则结点总数n=n0+n1+n2.即n0=n2+1。
2、非空二叉树的第K层最多有个结点。
3、高度为h的二叉树至多有个结点。
4、 
6.2.3二叉树的存储结构
顺序存储
链式存储
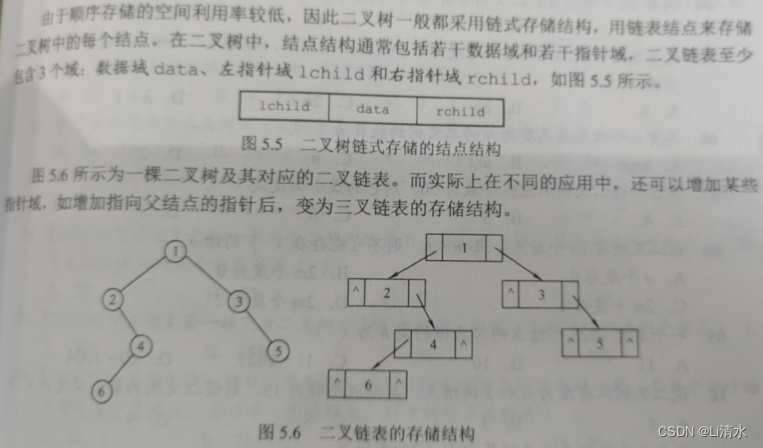
6.2.4二叉树的遍历
1、先序遍历
若二叉树为空，则什么都不做；否则，
访问根结点；
先序遍历左子树；
先序遍历右子树；
2、中序遍历
3、后序遍历
4、层次遍历
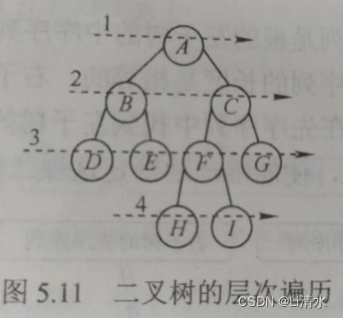
遍历顺序为：A B C D E F G H I
6.2.5由遍历序列确定二叉树
已知中序序列，再给出其他三种遍历序列中的任意一种，就可以唯一地确定一颗二叉树。
1、先序加中序
在先序序列中，第一个结点一定是二叉树的根节点；
在中序序列中，根节点将中序序列分成左子树和右子树的中序序列；
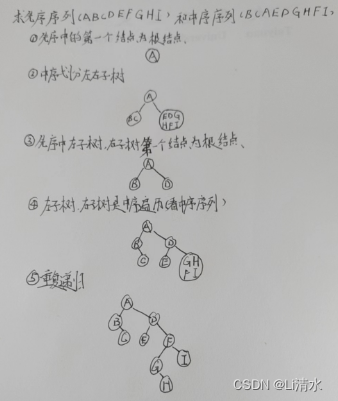
2、后序加中序
后序序列的最后一个结点为根结点，其余与前序加中序类似。
3、层序加中序
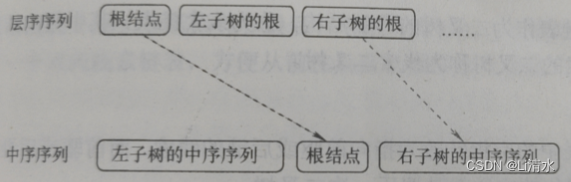
6.3线索二叉树
第7章图
图的定义
有向图：
无向图：
简单图：1、不存在重复边2、不存在顶点到自身的边（无环）。
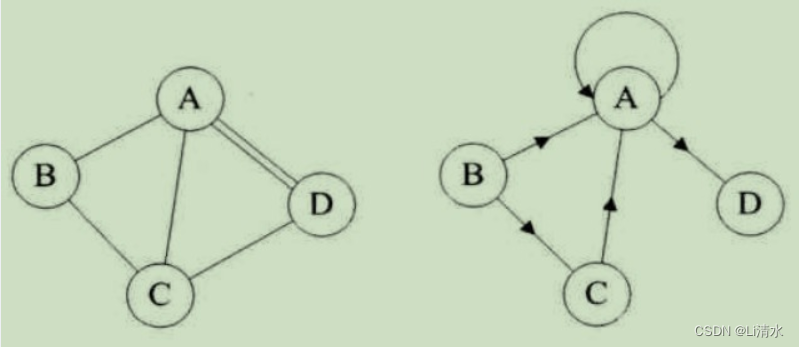多重图：某两结点之间边数多于一条；允许顶点通过一条边和自己关联。
完全图：
对于无向图，有n（n-1）/2条边的无向图称为完全图。（任意两个顶点之间都存在边）
对于有向图，有n（n-1）条弧的有向图称为完全图。（任意两个顶点之间都存在方向相反的两条弧）
子图：顶点数和边数都少。
生成子图（极大连通子图）：就是图本身。
连通图：
连通分量：无向图中的极大连通子图称为连通分量。
强连通图：有向图中，任意一对顶点都是强连通（v到w和从w到v之间都有路径）。
生成树：对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。
顶点的度，入度和出度：
边的权和网：
稠密图，稀疏图：
路径，路径长度和回路：
简单路径：顶点不重复。
距离：最短路径长度，不存在路径则为无穷。
图的存储及操作
邻接矩阵
邻接表
十字链表
邻接多重表
第八章 排序
插入排序
直接插入
cpp
void InsertSort(int A[],int n){
int i,j;
for(i=2;i<=n;i++){
if(A[i]<A[i-1]){
A[0]=A[i];//将当前元素放入哨兵
for(j=i-1;A[0]<A[j];--j){
A[j+1]=A[j];//向后移位
}
A[j+1]=A[0];//将当前元素插入
}
}
}空间效率：使用了个哨兵空间，因而空间复杂度为O（1）。
时间效率：最好情况（不用调整）O（n）；最坏情况O（n²）。
折半插入
cpp
void InsertSort(int A[],int n){
int i,j,min,mid,max;
for(i=2;i<=n;i++){
A[0]=A[i];//将当前元素放入哨兵
min=1;max=i-1;
while(min<=max){//无论如何都要折半查找
mid=(min+max)/2;
if(A[mid]>A[0]){
max=mid-1;
} else{
min=mid+1;
}
}
for(j=i-1;j>=max;--j){//向后移位
A[j+1]=A[j];
}
A[max+1]=A[0];
}
}空间效率：使用了个哨兵空间，因而空间复杂度为O（1）。
时间效率：O（n²）。
希尔排序
cpp
void ShellSort(int A[],int n){
int dk,i,j;
for(dk=n/2;dk>=1;dk=dk/2){//确定增量变化
for(i=dk+1;i<=n;i++){//从数组中间向后遍历
if(A[i]<A[i-dk]){
A[0]=A[i];
for(j=i-dk;j>0&&A[0]<A[j];j-=dk){//向后移位
A[j+dk]=A[j];
}
A[j+dk]=A[0];
}
}
}
}空间效率：使用了个暂存空间，因而空间复杂度为O（1）。
时间效率：当n在某个特定范围时O（);最坏情况O（n²）。
交换排序
冒泡排序
cpp
void BubbleSort(int A[],int n){
for(int i=0;i<n-1;i++){//一遍使最大值在第一个，n遍排好
bool flag=false;//表示本趟冒泡是否发生交换的标志
for(int j=n-1;j>i;j--){
if(A[j-1]>A[j]){
int m=A[j-1];
A[j-1]=A[j];
A[j]=m;
flag=true;
}
}
if(flag==false)//如果不需要调整
return;
}
}空间效率：使用了个暂存空间，因而空间复杂度为O（1）。
时间效率：最好情况O（n）;最坏情况O（n²）；平均时间O（n²）。
快速排序
cpp
#include <stdio.h>
int partition(int arr[], int low, int high);
void swap(int *xp, int *yp);
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
// 递归排序左半部分
quickSort(arr, low, pi - 1);
// 递归排序右半部分
quickSort(arr, pi + 1, high);
}
}
// 用于快速排序的辅助函数，用于分区
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = (low - 1); // 初始化指向比基准小的元素的指针
for (int j = low; j <= high - 1; j++) {
// 如果当前元素小于或等于基准，则交换元素
if (arr[j] <= pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]); // 将基准元素放在正确的位置
return (i + 1);
}
// 交换两个元素
void swap(int *xp, int *yp) {
int temp = *xp;
*xp = *yp;
*yp = temp;
}
int main() {
int arr[] = {12, 23, 28, 35, 37, 39, 50, 60, 78, 90};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
printf("排序后的数组：\n");
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}空间效率：O(log n)；这里 log n 是因为递归调用栈的最大深度是 log n（每个递归调用都会将问题规模减半，直到问题规模小于或等于1）。
时间效率：最坏情况O（n²）；平均时间O(n log n)。