数据结构：N叉树 (N-ary Tree)

从二叉到N叉 (Generalization)

严格N叉树 (Strict N-ary Tree)

[N叉树的高度 vs 节点数](#N叉树的高度 vs 节点数)

通用N叉树

严格N叉树

[严格N叉树的内部 vs 外部节点](#严格N叉树的内部 vs 外部节点)

总结

我们继续将二叉树的概念推广到更普遍的情况------N叉树 (N-ary Tree)。这会让你看到之前学到的所有二叉树性质，实际上都只是N=2时的特例。

从二叉到N叉 (Generalization)

我们知道，"二叉 (Binary)"的含义是"2"。二叉树就是一个节点最多有2个孩子的树。
如果我们把这个数字"2"换成一个通用的变量 n，会发生什么？
这就自然地推导出了N叉树的定义：一个节点最多可以有 n 个孩子。
N叉树 (N-ary Tree): 在这种树中，任何节点最多有 n 个子节点。n 是一个大于等于0的整数，代表树的"度 (degree)"或"叉数 (arity)"。
- n=0: 空树。
- n=1: 本质上是一个链表 (Linked List)。
- n=2: 就是我们熟悉的二叉树 (Binary Tree)。
- n=3: 称为三叉树 (Ternary Tree)。

C/C++ 代码表示 : 在二叉树中，我们用 left 和 right 两个指针。

但在N叉树中，孩子的数量是可变的。所以，最灵活的表示方式是使用一个指针数组（或在C++中使用vector，但我们遵循"不使用STL"的约定，所以会用指针数组）。

cpp 复制代码

// 假设n是已知的常量，比如 #define N 3
struct TreeNode {
    int data;
    TreeNode* children[N]; // 一个固定大小的指针数组
};

// 如果n不是固定的，则需要更动态的结构
struct DynamicTreeNode {
    int data;
    int num_children;
    DynamicTreeNode** children; // 一个指向指针数组的指针
};

严格N叉树 (Strict N-ary Tree)

回顾严格二叉树，我们去掉了"度为1"这个中间状态，只保留"度为0"和"度为2"。
推广: 对于N叉树，我们同样去掉所有的中间状态（度为1, 2, ..., n-1），只保留两个极端：
1. 度为0: 节点是叶子节点。
2. 度为n : 节点是内部节点，且必须有 n 个孩子。
定义:

在严格N叉树中，任何节点要么是叶子（0个孩子），要么恰好有 n 个孩子。

N叉树的高度 vs 节点数

我们用 n 替换之前推导中的 2。

通用N叉树

A. 最大节点数 n_max (给定高度 h)

原理: 把每一层都用 n 个孩子填满。
推导:
- 第0层: n^0 = 1 个节点
- 第1层: n^1 = n 个节点
- 第i层: n^i 个节点
- 总数是等比数列求和: fraca(r^k − 1) r − 1。这里首项为1，公比为n，项数为h+1。

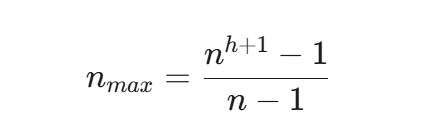
B. 最小节点数 n_min (给定高度 h)

原理: 形成一条"链"，不产生任何多余分支。
推导: 和二叉树一样，为了达到高度h，最少需要 h+1 个节点连成一条线。
公式:

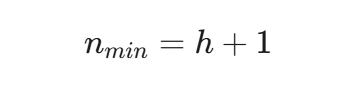
严格N叉树

A. 最大节点数 n_max (给定高度 h)

原理: "最胖"的严格N叉树就是每一层都填满的完美N叉树，它天然满足严格N叉树的定义。
结论: 与通用N叉树的最大节点数情况完全相同。

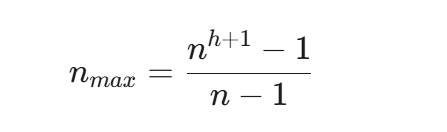
B. 最小节点数 n_min (给定高度 h)

原理 : 达到高度h，同时满足"0或n"规则，并使用最少节点。
推导:
- 我们需要一条长度为 h 的主路径。这条路径上有 h+1 个节点。
- 从根节点开始，路径上的前 h 个节点都不能是叶子，所以它们必须是内部节点，每个节点都要生出 n 个孩子。
- 为了最节省节点，我们让其中1个孩子作为主路径的延伸，另外 n-1 个孩子都直接作为叶子。
- 我们来算一下总节点数：
  - h = 0: 1个节点（根节点本身就是叶子）。
  - h = 1: 根节点必须是内部节点，它有n个孩子（都是叶子）。总节点数 = 1 + n。
  - h = 2: 在h = 1的基础上，选择一个叶子，让它变成内部节点，再生出n个孩子。为了达到高度2，这个操作必须执行一次。
    - 总节点数 = (原来的节点数) + (新增的 n 个孩子) = 1 + n + n = 1 + 2n。

cpp 复制代码

●(叶子)

cpp 复制代码

   ●(I)
  / | \
 ●  ●  ●  ... 共 n 个

cpp 复制代码

   ●(I)
  / | \
 ●  ●  ●  ... 共 n 个
 ↑
 选中它作为主路径延伸
     |
     ●(I)
    / | \
   ●  ●  ●  ... 共 n 个

规律: 从h=0的一个节点开始，为了让高度增加1，都需要选择一个叶子，给它n个孩子，这个过程净增加n个节点。要达到高度h，需要进行h次这样的操作。

公式：

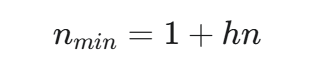
验证 : 当n = 2时，公式变为 1 + 2h，与严格二叉树的结论完全一致。

严格N叉树的内部 vs 外部节点

这是将 E = I + 1 推广到N叉的优美结论。

设 I 为内部节点数，E 为外部节点（叶子）数。

第一性原理 (通过数"边"的两种方法) 这个推导方法非常巧妙且具有普适性。

从"父节点"的视角数边:

在严格N叉树中，只有内部节点才有孩子。
每个内部节点（共 I 个）都伸出 n 条边连接到它的孩子。
所以，总的边的数量是 I

从"子节点"的视角数边:

在任何树形结构中，除了根节点，每个节点都有且仅有一个父节点。
因此，每个节点（除了根）都有一条指向它的边。
如果总节点数是 N，那么总的边的数量就是 N−1。

建立等式:

两种方法数出来的边数必然相等：

I × n = N − 1
我们又知道，总节点数是内部节点和外部节点之和：N = I + E。
将 N 代入上面的等式：

I × n = (I + E) − 1
现在，我们整理这个等式来寻找 I 和 E 的关系：

I × n − I + 1 = E

E = I (n − 1) + 1

结论: 对于任何非空严格N叉树，外部节点数 E 和内部节点数 I 的关系为 E = I (n − 1) + 1。

验证 : 当n=2（严格二叉树）时，公式变为 E = I (2 − 1) + 1RightarrowE = I + 1。完美符合我们之前的结论！

总结

我们将二叉树的所有性质都成功推广到了N叉树，并看到它们是更一般规律的特例。

特性	通用N叉树 (General N-ary Tree)	严格N叉树 (Strict N-ary Tree)
节点度定义	len	0 或 n
高度`h` vs 节点`n`	n_min=h+1 <br> n_max=fracnh+1−1n−1	n_min=1+hn <br> n_max=fracnh+1−1n−1
内部`I` vs 外部`E`	(无简单关系)	E=I(n−1)+1

这些从第一性原理出发的推导，不仅给了你公式，更重要的是让你理解了这些公式背后的结构性约束，这样你就能在面对更复杂的问题时，自己去分析和推导。