【线性代数】第七章-二次型

文章目录

[一. 基本内容与重要结论](#一. 基本内容与重要结论)
- [1. 二次型、二次型矩阵](#1. 二次型、二次型矩阵)
- [2. 标准型与规范型](#2. 标准型与规范型)
- [3. 惯性指数](#3. 惯性指数)
- [4. 坐标变换](#4. 坐标变换)
- [5. 矩阵合同](#5. 矩阵合同)
- [6. 正定矩阵与正定二次型](#6. 正定矩阵与正定二次型)
[二. 主要定理](#二. 主要定理)
- [1. 二次型变换为标准型的相关定理](#1. 二次型变换为标准型的相关定理)
- - [1.1. 二次型的坐标变换](#1.1. 二次型的坐标变换)
  - [1.2. 任意二次型都可变换为标准型](#1.2. 任意二次型都可变换为标准型)
  - 1.3.二次型的矩阵（就是是实对称矩阵）总可以合同一个对角矩阵
  - [1.4. 实对称矩阵总可以（通过正交变换）化成标准形](#1.4. 实对称矩阵总可以（通过正交变换）化成标准形)
- [2. 惯性定理](#2. 惯性定理)
- [3. 二次型正定的充要条件](#3. 二次型正定的充要条件)

二次型的两大板块要复习整理清楚，一个是标准形，另一个是正定性.

了解二次型的概念，掌握用矩阵形式表示二次型，了解合同变换和合同矩阵的概念.

理解二次型秩的概念，

了解二次型的标准形、规范形等概念

了解惯性定理的条件和结论，掌握用正交变换化二次型为标准形的方法

了解用配方法化二次型为标准形的方法

理解正定二次型、正定矩阵的概念，掌握正定矩阵的性质。

一. 基本内容与重要结论

1. 二次型、二次型矩阵

注意：二次型规定，aij=aji，也就是二次型的矩阵是对称矩阵。

2. 标准型与规范型

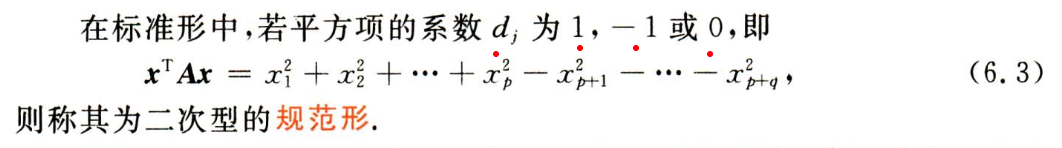
3. 惯性指数

4. 坐标变换

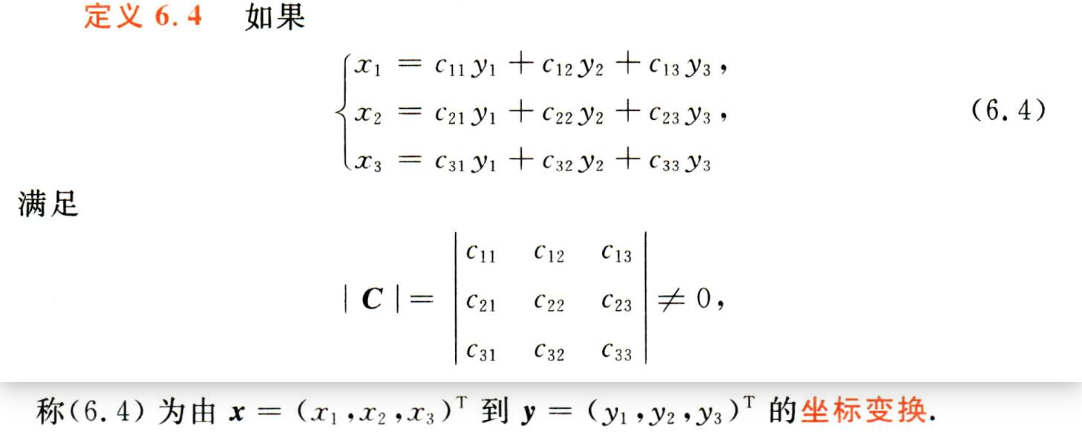
5. 矩阵合同

合同的传递性。

6. 正定矩阵与正定二次型

A如果是正定矩阵则A=A的转置，就是对称矩阵其实。

二. 主要定理

1. 二次型变换为标准型的相关定理

1.1. 二次型的坐标变换

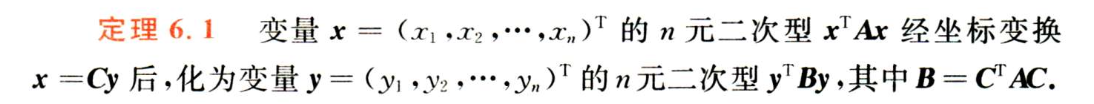
B不一定是对角矩阵。

shell 复制代码

若矩阵A与矩阵B均为n阶方阵，则A与B相似的必要条件为：
1、A与B的特征值相同。
2、λE-A与λE-B等价。
3、tr(A)=tr(B)。 对角元素之和
4、|A|=|B|。

1.2. 任意二次型都可变换为标准型

1.3.二次型的矩阵（就是是实对称矩阵）总可以合同一个对角矩阵

1.4. 实对称矩阵总可以（通过正交变换）化成标准形

能够化成标准型说明了几个信息:

通过正交变换后的矩阵是对角矩阵；
变换后的矩阵，与变换前的矩阵相似且合同。

求标准型就是求矩阵的特征值。

2. 惯性定理

合同则有相同规范型，p、q个数不变。

3. 二次型正定的充要条件

（2）：说明二次型能化成规范型