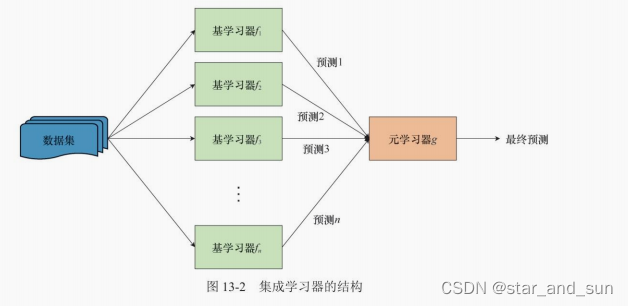
集成学习
不同的算法都可以对解决同一个问题,但是可能准确率不同,集成学习就是不同算法按照某种组合来解决问题,使得准确率提升。
那怎么组合算法呢?
自举聚合算法 **(bagging)**
顾名思义是 自举+聚合
自举是指的是自举采样,保证随机性,允许重复的又放回抽样,每次抽与原样本大小相同的样本出来,如果进行B次。则有B个数据集,然后独立的训练出模型 f(x) ,求得平均值
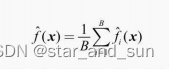
对于低偏差、高方差模型的稳定性有较大提升
随机森林
bagging算法的改进版就是随机森林
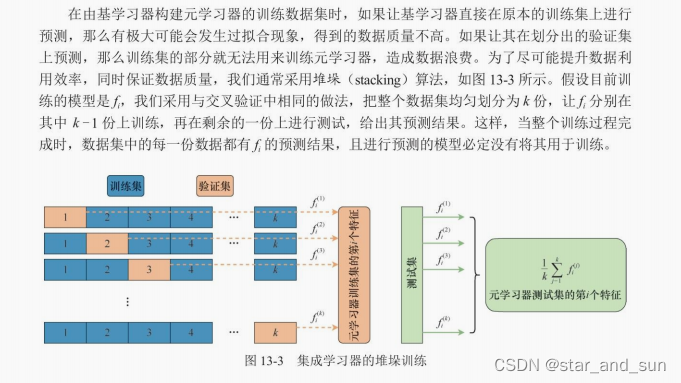

c
from tqdm import tqdm
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.model_selection import train_test_split
# 创建随机数据集
X, y = make_classification(
n_samples=1000, # 数据集大小
n_features=16, # 特征数,即数据维度
n_informative=5, # 有效特征个数
n_redundant=2, # 冗余特征个数,为有效特征的随机线性组合
n_classes=2, # 类别数
flip_y=0.1, # 类别随机的样本个数,该值越大,分类越困难
random_state=0 # 随机种子
)
print(X.shape)
#%%
class RandomForest():
def __init__(self, n_trees=10, max_features='sqrt'):
# max_features是DTC的参数,表示结点分裂时随机采样的特征个数
# sqrt代表取全部特征的平方根,None代表取全部特征,log2代表取全部特征的对数
self.n_trees = n_trees
self.oob_score = 0
self.trees = [DTC(max_features=max_features)
for _ in range(n_trees)]
# 用X和y训练模型
def fit(self, X, y):
n_samples, n_features = X.shape
self.n_classes = np.unique(y).shape[0]
# 集成模型的预测,累加单个模型预测的分类概率,再取较大值作为最终分类
ensemble = np.zeros((n_samples, self.n_classes))
for tree in self.trees:
# 自举采样,该采样允许重复
idx = np.random.randint(0, n_samples, n_samples)
# 没有被采到的样本
unsampled_mask = np.bincount(idx, minlength=n_samples) == 0
unsampled_idx = np.arange(n_samples)[unsampled_mask]
# 训练当前决策树
tree.fit(X[idx], y[idx])
# 累加决策树对OOB样本的预测
ensemble[unsampled_idx] += tree.predict_proba(X[unsampled_idx])
# 计算OOB分数,由于是分类任务,我们用正确率来衡量
self.oob_score = np.mean(y == np.argmax(ensemble, axis=1))
# 预测类别
def predict(self, X):
proba = self.predict_proba(X)
return np.argmax(proba, axis=1)
def predict_proba(self, X):
# 取所有决策树预测概率的平均
ensemble = np.mean([tree.predict_proba(X)
for tree in self.trees], axis=0)
return ensemble
# 计算正确率
def score(self, X, y):
return np.mean(y == self.predict(X))
#%%
# 算法测试与可视化
num_trees = np.arange(1, 101, 5)
np.random.seed(0)
plt.figure()
# bagging算法
oob_score = []
train_score = []
with tqdm(num_trees) as pbar:
for n_tree in pbar:
rf = RandomForest(n_trees=n_tree, max_features=None)
rf.fit(X, y)
train_score.append(rf.score(X, y))
oob_score.append(rf.oob_score)
pbar.set_postfix({
'n_tree': n_tree,
'train_score': train_score[-1],
'oob_score': oob_score[-1]
})
plt.plot(num_trees, train_score, color='blue',
label='bagging_train_score')
plt.plot(num_trees, oob_score, color='blue', linestyle='-.',
label='bagging_oob_score')
# 随机森林算法
oob_score = []
train_score = []
with tqdm(num_trees) as pbar:
for n_tree in pbar:
rf = RandomForest(n_trees=n_tree, max_features='sqrt')
rf.fit(X, y)
train_score.append(rf.score(X, y))
oob_score.append(rf.oob_score)
pbar.set_postfix({
'n_tree': n_tree,
'train_score': train_score[-1],
'oob_score': oob_score[-1]
})
plt.plot(num_trees, train_score, color='red', linestyle='--',
label='random_forest_train_score')
plt.plot(num_trees, oob_score, color='red', linestyle=':',
label='random_forest_oob_score')
plt.ylabel('Score')
plt.xlabel('Number of trees')
plt.legend()
plt.show()提升算法
提升算法是另一种集成学习的框架,思路是利用当前模型的偏差来调整训练数据的权重

适应提升


from sklearn.ensemble import AdaBoostClassifier
cpp
# 初始化stump
stump = DTC(max_depth=1, min_samples_leaf=1, random_state=0)
# 弱分类器个数
M = np.arange(1, 101, 5)
bg_score = []
rf_score = []
dsc_ada_score = []
real_ada_score = []
plt.figure()
with tqdm(M) as pbar:
for m in pbar:
# bagging算法
bc = BaggingClassifier(estimator=stump,
n_estimators=m, random_state=0)
bc.fit(X_train, y_train)
bg_score.append(bc.score(X_test, y_test))
# 随机森林算法
rfc = RandomForestClassifier(n_estimators=m, max_depth=1,
min_samples_leaf=1, random_state=0)
rfc.fit(X_train, y_train)
rf_score.append(rfc.score(X_test, y_test))
# 离散 AdaBoost,SAMME是分步加性模型(stepwise additive model)的缩写
dsc_adaboost = AdaBoostClassifier(estimator=stump,
n_estimators=m, algorithm='SAMME', random_state=0)
dsc_adaboost.fit(X_train, y_train)
dsc_ada_score.append(dsc_adaboost.score(X_test, y_test))
# 实 AdaBoost,SAMME.R表示弱分类器输出实数
real_adaboost = AdaBoostClassifier(estimator=stump,
n_estimators=m, algorithm='SAMME.R', random_state=0)
real_adaboost.fit(X_train, y_train)
real_ada_score.append(real_adaboost.score(X_test, y_test))
# 绘图
plt.plot(M, bg_score, color='blue', label='Bagging')
plt.plot(M, rf_score, color='red', ls='--', label='Random Forest')
plt.plot(M, dsc_ada_score, color='green', ls='-.', label='Discrete AdaBoost')
plt.plot(M, real_ada_score, color='purple', ls=':', label='Real AdaBoost')
plt.xlabel('Number of trees')
plt.ylabel('Test score')
plt.legend()
plt.tight_layout()
plt.savefig('output_26_1.png')
plt.savefig('output_26_1.pdf')
plt.show()
#%%GBDT算法
GBDT算法中应用广泛的是XGBoost,其在损失函数中添加与决策树复杂度相关的正则化约束,防止单个弱学习发生过拟合现象。
cpp
# 安装并导入xgboost库
!pip install xgboost
import xgboost as xgb
from sklearn.datasets import make_friedman1
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import BaggingRegressor, RandomForestRegressor, \
StackingRegressor, AdaBoostRegressor
# 生成回归数据集
reg_X, reg_y = make_friedman1(
n_samples=2000, # 样本数目
n_features=100, # 特征数目
noise=0.5, # 噪声的标准差
random_state=0 # 随机种子
)
# 划分训练集与测试集
reg_X_train, reg_X_test, reg_y_train, reg_y_test = \
train_test_split(reg_X, reg_y, test_size=0.2, random_state=0)
#%%
def rmse(regressor):
# 计算regressor在测试集上的RMSE
y_pred = regressor.predict(reg_X_test)
return np.sqrt(np.mean((y_pred - reg_y_test) ** 2))
# XGBoost回归树
xgbr = xgb.XGBRegressor(
n_estimators=100, # 弱分类器数目
max_depth=1, # 决策树最大深度
learning_rate=0.5, # 学习率
gamma=0.0, # 对决策树叶结点数目的惩罚系数,当弱分类器为stump时不起作用
reg_lambda=0.1, # L2正则化系数
subsample=0.5, # 与随机森林类似,表示采样特征的比例
objective='reg:squarederror', # MSE损失函数
eval_metric='rmse', # 用RMSE作为评价指标
random_state=0 # 随机种子
)
xgbr.fit(reg_X_train, reg_y_train)
print(f'XGBoost:{rmse(xgbr):.3f}')
# KNN回归
knnr = KNeighborsRegressor(n_neighbors=5).fit(reg_X_train, reg_y_train)
print(f'KNN:{rmse(knnr):.3f}')
# 线性回归
lnr = LinearRegression().fit(reg_X_train, reg_y_train)
print(f'线性回归:{rmse(lnr):.3f}')
# bagging
stump_reg = DecisionTreeRegressor(max_depth=1,
min_samples_leaf=1, random_state=0)
bcr = BaggingRegressor(estimator=stump_reg,
n_estimators=100, random_state=0)
bcr.fit(reg_X_train, reg_y_train)
print(f'Bagging:{rmse(bcr):.3f}')
# 随机森林
rfr = RandomForestRegressor(n_estimators=100, max_depth=1,
max_features='sqrt', random_state=0)
rfr.fit(reg_X_train, reg_y_train)
print(f'随机森林:{rmse(rfr):.3f}')
# 堆垛,默认元学习器为带L2正则化约束的线性回归
stkr = StackingRegressor(estimators=[
('knn', knnr),
('ln', lnr),
('rf', rfr)
])
stkr.fit(reg_X_train, reg_y_train)
print(f'Stacking:{rmse(stkr):.3f}')
# 带有输入特征的堆垛
stkr_pt = StackingRegressor(estimators=[
('knn', knnr),
('ln', lnr),
('rf', rfr)
], passthrough=True)
stkr_pt.fit(reg_X_train, reg_y_train)
print(f'带输入特征的Stacking:{rmse(stkr_pt):.3f}')
# AdaBoost,回归型AdaBoost只有连续型,没有离散型
abr = AdaBoostRegressor(estimator=stump_reg, n_estimators=100,
learning_rate=1.5, loss='square', random_state=0)
abr.fit(reg_X_train, reg_y_train)