文章目录
引言
复习
(单调队列优化DP)------最大子序和
- 这个已经是第二天做了,昨天基本上已经做了很多推理,今天就要把这道题完成,下述是昨天的学习的链接
- 单调递增队列的推理
- 昨天经过推理,知道了要将这个问题进行转换,由原先的特定长度和的最大值,转成求特定长度和的最小值。然后通过画图证明了,为什么要通过单调队列实现最小值的计算。
- 今天主要是关注代码的执行。
单调队列的基本实现思路------求可移动窗口中的最值
- 使用队列维系一个集合m
- 将无用的元素从后往前进行排除,保证队列是一个单调递增的队列
- 找出最大值或者最小值
在这里的队列保存的元素是的特定序列的累加和,不是具体的元素的大小,保证单调递增!!
- 这个代码不是那么好懂,我自己再写一遍。
c
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 300010;
int q[N],s[N];
int n,m;
int main(){
cin>>n>>m;
for (int i = 1; i <= n ; ++i) {
cin>>s[i];
s[i] += s[i - 1];
}
// 创建对应的队列
int hh = 0,tt = 0,res = INT_MIN;
q[hh] = 0;
for (int i = 1; i <= n; ++i) {
// 保证队列的长度不变
if (i - hh > m) hh++;
// 计算最值
res = max(res , s[i] - s[q[hh]]);
// 更新的队列尾部
// 队列可为空,也就是tt >= hh
// 然后就是保证队列是单调递增的,如果出现新的值小于后续的值,
// 就要将所有比之大的数据排除,因为是一个序列,一定会选中这个数据
while(tt >= hh && s[q[tt]] > s[i]) tt --;
// 移动到一个小于或者等于的数字之后,tt再往后移动一个,即将新的排序值,加入其中。
q[++tt] = i;
}
cout<<res;
}总结
- 重新写了一遍,效果好多了,并没有像之前那么难以理解了,主要有两个地方需要好好整理一下,分别是
- 这里的单调递增是针对S,也就是每一个前序和来说的,不是针对特定的某一个元素说的。
- 这里使用一个数组模拟队列,hh模拟队列的头指针,tt模拟队列的尾指针
- hh头指针只需要保证是最小值,并且队列的长度不超过m
- tt尾指针需要覆盖新的元素,保证整个队列是单调递增的,因为这是一个序列和,如果后续的序列和比前面的小,那么最终就不一定不会选择前面的序列和。
背包模型------宠物小精灵收服问题

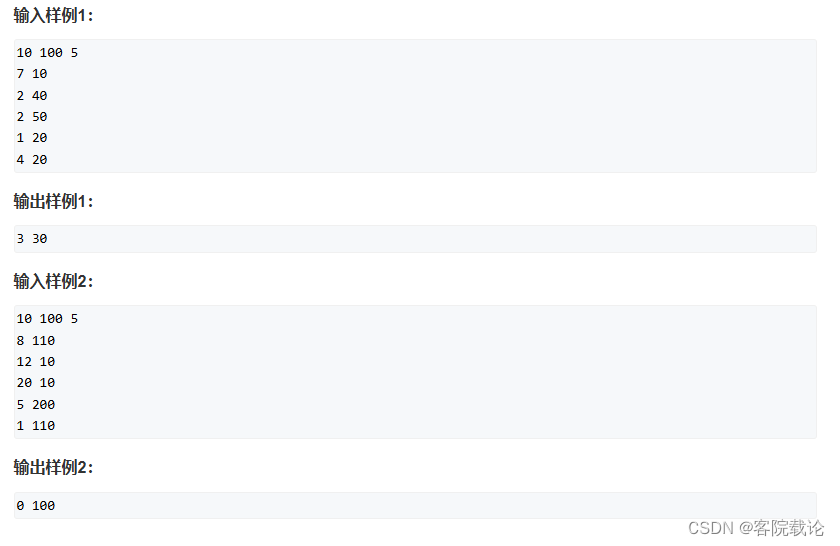
思路分析
-
这道题是经典的背包模型问题,收服的精灵就是要求在特定空间下装的货越多,然后的皮卡丘收到的伤害就是代价越小越好,
-
每一个状态的集合,主要分为两个部分,收取当前的精灵和不收取当前的精灵,而且要同时满足两个约束的,就是最多收服精灵的个数,皮卡丘最少收到的伤害,不过究竟哪个更加重要?明白了,尽可能多的精灵,然后同样多的情况下,保证尽可能多的剩余体力。所以,这里要两个矩阵
- 一个保存数量,这个属性值,也是dp的主要目标
- 另外一个保存剩余的体力值,这个用来后续判断
-
感觉有点不对,这里是不是要再增加一个新的遍历条件,也就是体力值?如果不增加就没有意义了。
-
暂时实现成这样了,还有点问题,不过时间不够了,直接看代码了
c
#include <iostream>
using namespace std;
const int N = 1010,M = 505,K = 105; // N是精灵球的数量,M是皮卡丘的体力值,K是野生小精灵的数量
int f[K][N],mr[K][N],n1[K],m1[K];
int n,m,k;
int main(){
cin>>n>>m>>k;
for (int i = 1; i < k; ++i) {
cin>>n1[i]>>m1[i];
}
// 遍历对应的数据
for (int i = 1; i < k; ++i) {
for (int j = 0; j < N; ++j) {
f[i][j] = 0;
// 两种状态,
// 一种是收服当前的精灵,f[i-1][j - n1[i]] + 1
// 判定当前剩余的体力以及精灵球的数量是否满足要求
if (m >= m1[i] && k >= n1[i])
f[i][j] = f[i-1][j - n1[i]] + 1;
// 另外一种是不收服当前的精灵,f[i-1][j]
int temp = f[i-1][j];
if (temp > f[i][j]){
// 不收服的结果大于当前的结果
f[i][j] = temp;
}else{
m -= m1[i];
n -= n1[i];
}
}
}
// 输出最终的结果,遍历一下
}参考思路分析
- 这里是二维背包问题,需要考虑两个维度,所以我上面的思路有问题,应该使用二维背包去解决这个问题。
- 这里先直接贴代码,参考分析一下
- 二维背包,然后使用滚动数组进行优化
- 然后遍历最后一个维度下,精灵球最多的情况下,体力值消耗最小的情况。
- 还是得看看之前的背包问题咋写的,一维和二维之间的相互转换。
c
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = 1010, K = 510;
int n, m, t;
int v1[N], v2[N];
int f[M][K];
int main()
{
//input
cin >> m >> t >> n;
for (int i = 1; i <= n; ++ i) cin >> v1[i] >> v2[i];
//dp
for (int i = 1; i <= n; ++ i)
{
for (int j = m; j >= v1[i]; -- j)
{
for (int k = t - 1; k >= v2[i]; -- k)
{
f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
}
}
}
//output
cout << f[m][t - 1] << " ";
//找到满足最大价值的所有状态里,第二维费用消耗最少的
int cost_health = t;
for (int k = 0; k <= t - 1; ++ k)
{
if (f[m][k] == f[m][t - 1])
{
cost_health = min(cost_health, k);
}
}
cout << t - cost_health << endl;
return 0;
}作者:一只野生彩色铅笔
链接:https://www.acwing.com/solution/content/52741/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
新作
- 今天晚上会进行的某公司的主管面,今天新做的题目就是主管面的手撕算法题。
二叉树的后续遍历加指针调换
- 这道题吃亏在于我没有看清楚题目,没有理解他的题目,我觉得他说的比较混乱,而且有一个东西感觉没有任何意义。
- 不过我也发现我的问题了,二叉树定义哪里有问题,没有实现的好。
- 下面是我写的, 大概是写对的
c
#include <iostream>
#include <vector>
using namespace std;
struct Node{
int val;
Node* left;
Node* right;
Node(int x):val(x),left(NULL),right(NULL){};
};
vector<int> res;
void dfs(Node* root){
if (root->left) dfs(root->left);
if (root->right) dfs(root->right);
res.push_back(root->val);
}
int main(){
Node* root =new Node(1);
dfs(root);
for(int i = 0;i < res.size();i ++)
cout<<res[i]<<",";
delete root;
}针对第二个问题,表述如下
-
要将二叉树的左右子节点更换为后序遍历中的左右子节点,并且更改之后的结果可能不是一个树,甚至有可能成为其他结构。
-
其实我蛮不能理解他的用意的,究竟是让我干什么?把一个二叉树的左右子节点变为后续遍历顺序中的节点,那么指针的方向有没有改变?然后,构建出来是什么样?原来的结构还要保存吗?
-
如果只是单纯换一个方式,不就是在创建一个后序遍历的链表吗?把每一个节点都加进去不就行了吗?
-
现在还不是很懂这个题目
-
下面是ChatGPT写的,感觉没有什么意义。
c
#include <iostream>
#include <vector>
struct Node {
int val;
Node* left;
Node* right;
Node(int x) : val(x), left(nullptr), right(nullptr) {}
};
// 后序遍历,记录节点访问顺序
void postOrderDFS(Node* root, std::vector<Node*>& nodes) {
if (root == nullptr) {
return;
}
postOrderDFS(root->left, nodes);
postOrderDFS(root->right, nodes);
nodes.push_back(root);
}
// 根据后序遍历的节点顺序调整左右子节点
void adjustNodes(std::vector<Node*>& nodes) {
for (size_t i = 0; i < nodes.size() - 1; ++i) {
nodes[i]->left = nullptr;
nodes[i]->right = nodes[i + 1];
}
nodes.back()->left = nullptr;
nodes.back()->right = nullptr;
}
// 辅助函数:中序遍历打印二叉树
void inOrderPrint(Node* root) {
if (root == nullptr) {
return;
}
inOrderPrint(root->left);
std::cout << root->val << " ";
inOrderPrint(root->right);
}
// 辅助函数:后序遍历打印二叉树
void postOrderPrint(Node* root) {
if (root == nullptr) {
return;
}
postOrderPrint(root->left);
postOrderPrint(root->right);
std::cout << root->val << " ";
}
int main() {
// 创建一个简单的二叉树
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->right->left = new Node(6);
root->right->right = new Node(7);
std::cout << "Original tree (in-order): ";
inOrderPrint(root); // 预期输出: 4 2 5 1 6 3 7
std::cout << std::endl;
std::cout << "Original tree (post-order): ";
postOrderPrint(root); // 预期输出: 4 5 2 6 7 3 1
std::cout << std::endl;
// 后序遍历并记录节点顺序
std::vector<Node*> postOrderNodes;
postOrderDFS(root, postOrderNodes);
// 根据后序遍历顺序调整节点
adjustNodes(postOrderNodes);
std::cout << "Adjusted structure (in-order): ";
inOrderPrint(root); // 可能无法正确打印,因为树结构已改变
std::cout << std::endl;
std::cout << "Adjusted structure (post-order): ";
postOrderPrint(root); // 预期输出与原后序遍历顺序一致
std::cout << std::endl;
return 0;
}总结
- 面试很难受,不过我尽力了,算法也复习到了。不过反映出我的问题,就是很多东西看的不够细致,不够深入,先过一遍,后续再继续深化。时间不是很够,加油。