排序算法、堆排序、大顶堆、小顶堆、手写快排-215. 数组中的第K个最大元素、2336. 无限集中的最小数字

[215. 数组中的第K个最大元素](#215. 数组中的第K个最大元素)

题目链接及描述

题目分析

堆排序分析

215. 数组中的第K个最大元素

题目链接及描述

215. 数组中的第K个最大元素 - 力扣（LeetCode）

题目分析

堆排序分析

题目所述为找到第K个最大元素，首先想到使用Arrays.sort(nums); return nums $nums.length - k$ 即可解决，此时很好，可以回家等通知了。

第K个最大元素，如果创建一个小顶堆，堆顶元素为最小，并维护堆中元素个数为K，当nums数组遍历结束后，堆顶元素即为返回的元素。

在Java中创建小顶堆以及大顶堆可以使用线程的PrioriityQueue来实现：

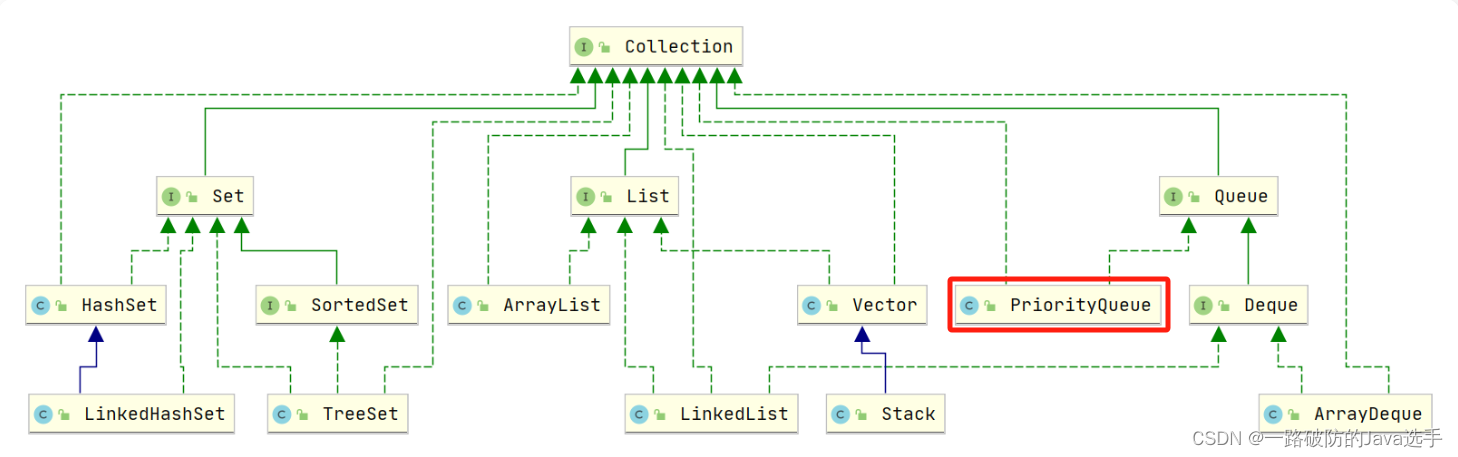
Java中的单列集合Collection及其实现类如上，通过上面图示，可以看到PriorityQueue就是Collection的一个实现类，创建代码参考如下：

java 复制代码

        PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->a - b);    //小顶堆
        PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->b - a);    //大顶堆

堆排序代码编写

java 复制代码

    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->a - b);
        for(int num : nums){
            if(pq.size() < k){
                pq.add(num);
            }else if(num > pq.peek()){
                pq.poll();
                pq.add(num);
            }
        }
        return pq.peek();
    }

这道题目如果在面试中出现的话，可能还是需要手写堆排序的，自己抽时间学习学习手写堆排序随后补充上。

快排分析

快排本质上就是对Arrays.sort(nums)的一种优化手段，具体可以网上查找资源，贴出自己编写的快排代码实现。

快排代码编写

java 复制代码

class Solution {
    public int findKthLargest(int[] nums, int k) {
        int len = nums.length;
        // 第1大的元素:len - 1;
        // 第2大的元素:len - 2;
        // 第k大的元素:len - k;
        mySort(nums, 0, len - 1);
        return nums[len - k];
    }
    public void mySort(int[] nums, int L, int R){
        if(L >= R)  return;
        int pivot = nums[L];
        int le = L + 1, ge = R;
        while(true){
            while(le <= ge && nums[le] < pivot) ++le;
            while(le <= ge && nums[ge] > pivot) --ge;
            if(le >= ge)    break;
            mySwap(nums, le, ge);
            ++le;
            --ge; 
        }
        mySwap(nums, L, ge);
        mySort(nums, L, ge - 1);
        mySort(nums, ge + 1, R);
    }
    public void mySwap(int[] nums, int idx1, int idx2){
        int temp = nums[idx1];
        nums[idx1] = nums[idx2];
        nums[idx2] = temp;
    }
}

2336、无限集中的最小数字

题目链接及描述

2336. 无限集中的最小数字 - 力扣（LeetCode）

题目分析

初次看到这个题目并没有将其和优先级队列联系起来，题目所述首先存储了所有正整数，随后popSmallest()和addBack()两个方法，对初始化的正整数数组进行操作。

int popSmallest() 移除并返回该无限集中的最小整数。
void addBack(int num) 如果正整数 num 不存在于无限集中，则将一个 num 添加到该无限集最后。

首先不可能创建一个数组或者List集合将所有正整数存储起来，想到的是设置一个标志位：如threshold，此值代表的含义为【threshold, +oo）这部分正整数尚未操作过，仍然存在于初始化数组中。【1，threshold)这部分数据已经从初始化数组中弹出。

此时对于addBack(int num)方法调用而言，只需要判断，num 和 threshold的关系，

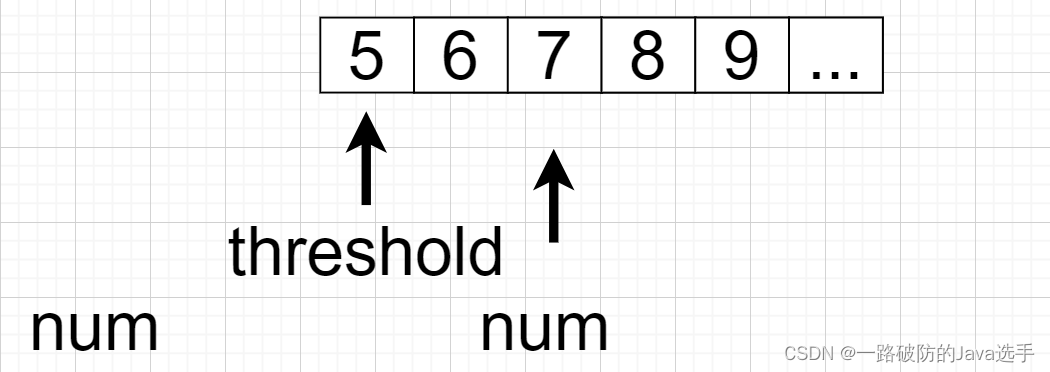
如果num > threshold，说明原集合中已经存在num，无法继续添加。
如果num < threshold，说明除初始集合中已经不存在num，需要将其添加至集合中，由于初始使用一个值threshold代表集合，此时可以创建一个小顶堆和哈希表set用于存储num，只有set中不存在num时将num对应的数据分别添加到set和小顶堆中。【哈希表set只是判断元素num知否已经出现过，如果出现过，则不添加，否则添加】

int popSmallest() 移除元素的方法调用此时也分为两种情况即可。

如果小顶堆队列不为空，则获取小顶堆堆顶对应的元素，并将其弹出。将set中对应的元素remove（）掉，返回堆顶元素即可。
如果小顶堆此时为空，直接返回threshold++。即返回了当前对应的元素，同时又将当前对应元素从"集合"中删除。

代码编写

java 复制代码

class SmallestInfiniteSet {
    public int threshold;
    public PriorityQueue<Integer> pq;
    public Set<Integer> set;
    public SmallestInfiniteSet() {
        this.threshold = 1;
        this.pq = new PriorityQueue<>((a, b)->a - b);
        this.set = new HashSet<>();
    }
    
    public int popSmallest() {
        if(pq.size() > 0){
            set.remove(pq.peek());
            return pq.poll();
        }
        return threshold++;
    }
    
    public void addBack(int num) {
        if(num >= threshold){
            return;
        }
        if(!set.contains(num)){
            set.add(num);
            pq.add(num);
        }
    }
}
/**
 * Your SmallestInfiniteSet object will be instantiated and called as such:
 * SmallestInfiniteSet obj = new SmallestInfiniteSet();
 * int param_1 = obj.popSmallest();
 * obj.addBack(num);
 */