1.3自然语言的分布式表示-word2vec

文章目录

0基于计数的方法的问题
1什么是基于推理的方法
2神经网络中单词的表示
- [2.1 MatMul 层的实现](#2.1 MatMul 层的实现)
3简单word2vec的实现
- [3.1 CBOW模型的结构](#3.1 CBOW模型的结构)
- [3.2 CBOW模型的学习](#3.2 CBOW模型的学习)
- 3.3单词的分布式表示

代码都位于：nlp；

其他相关内容详见专栏：深度学习自然语言处理基础_骑着蜗牛环游深度学习世界的博客-CSDN博客；

本篇博客对应视频：

9-基于推理的方法进行单词的分布式表示-独热编码-前向计算反向传播实现简单的全连接层_哔哩哔哩_bilibili；

10-基于推理的方法-CBOW模型结构_哔哩哔哩_bilibili；

0基于计数的方法的问题

计数的方法是在整个语料库上计算共现矩阵、ppmi矩阵、进行SVD奇异值分解；语料库很大时这是非常耗时间的（这一点在之前PTB数据集上也可以看到，SVD分解时是需要等待一段时间的）；另外，当语料库发生变化时，计数的方法就需要重新对整个语料库进行计算，来更新单词的向量表示（因为语料库变化之后单词之间的共现情况就会发生变化），这成本也是非常高的
因此就有了基于推理的方法，即使用神经网络，每次一个批次数据进行学习，更新权重；这样当语料库发生变化时，只需要将变化的部分拿来学习即可，成本大大降低；

1什么是基于推理的方法

使用神经网络，构建神经网络模型；将数据输入到模型中，模型进行预测，并反复更新网络的权重
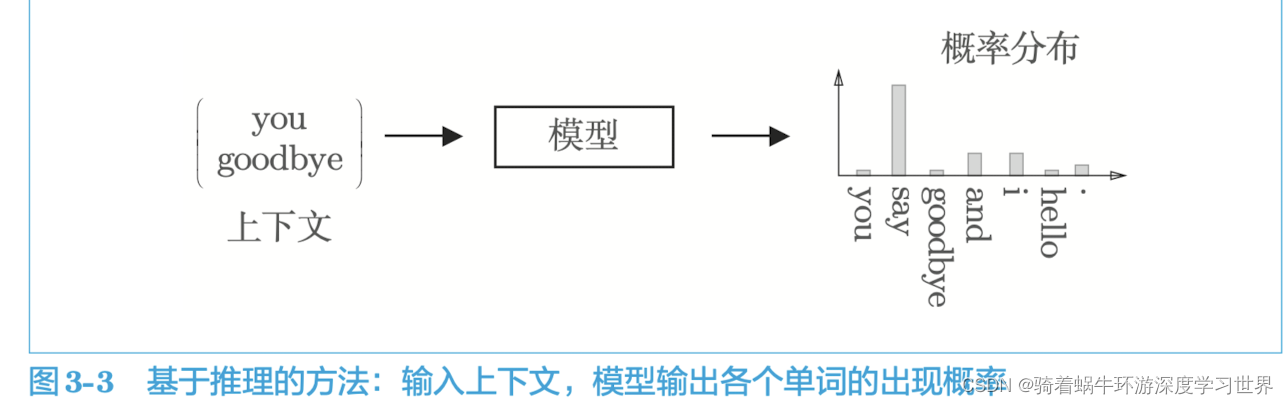
以下图为例，所谓的推理就是给定了单词的上下文，让模型去预测中间这个单词是什么；
1. 模型的输出将是一个关于各个可能单词的概率分布，概率最大的那个就是要预测的那个单词；
2. 通过不断地学习，模型逐渐能够准确预测这个单词是什么；
3. 那么就可以说，模型学习到了单词的出现模式 ，即++当周围出现某些单词的时候，中间的那个单词就会出现++。
4. 通过这种方式学习到的最终模型便可以用来进行单词的分布式表示（将结合后面的内容进行叙述）

2神经网络中单词的表示

要用神经网络处理单词，需要先将单词转化为固定长度的向量
一种方式为one-hot独热编码，只有一个元素是 1，其他元素都是 0
用"You say goodbye and I say hello."这个一句话的语料库来说明的话，这个语料库中，一共有 7 个单词，因此独热编码向量的长度就可以固定为7，每个单词都是长度为7的向量，并将单词 ID 对应的元素设为 1，其他元素设为 0；
向量固定下来之后，神经网络的输入层的神经元个数就固定下来了
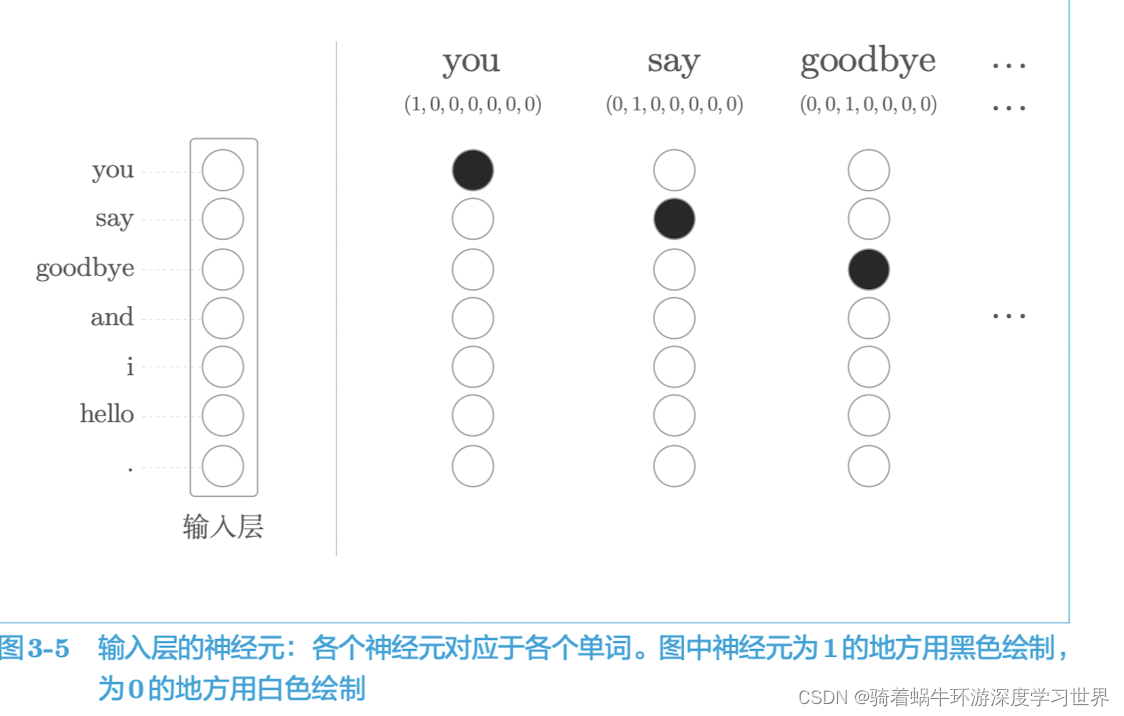
1. 输入层由 7 个神经元表示，分别对应于 7 个单词
2. 每个单词对应的单词向量的元素与这里的每个神经元一一对应
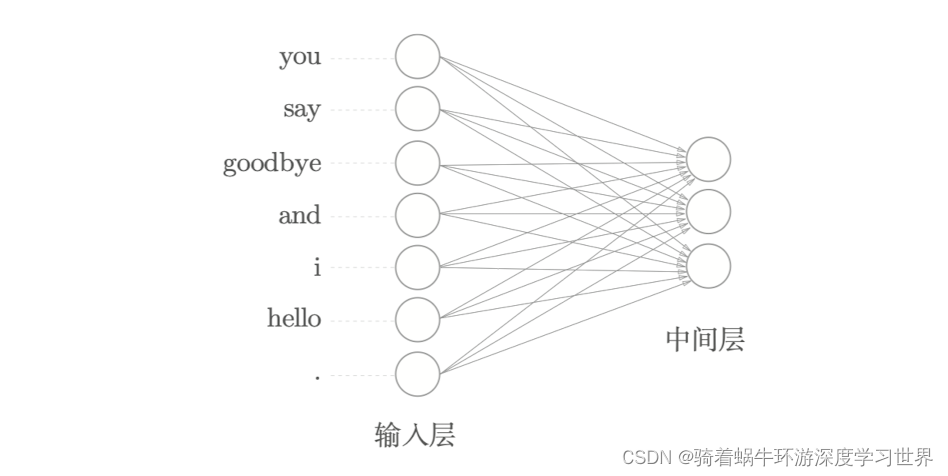
对于 one-hot 表示的某个单词，使用全连接层对其进行变换，如下图所示：
1. 每个箭头上都有权重
2. 权重和输入层神经元的加权和成为中间层的神经元
3. 这里省略了偏置，因此没有偏置的全连接层相当于在计算矩阵乘积
4. 对于某个单词的向量，其维度为[1,7]，经过全连接层（即每个输入层神经元都会参与到所有箭头的计算中）得到结果的维度为[1,3]，那么这里的箭头上的权重所构成的矩阵维度就是[7,3]
5. 如何理解计算过程：输入层的七个神经元与一组七个箭头上的权重对应相乘再相加，得到中间层第一个神经元的结果；以此类推；如下图所示：
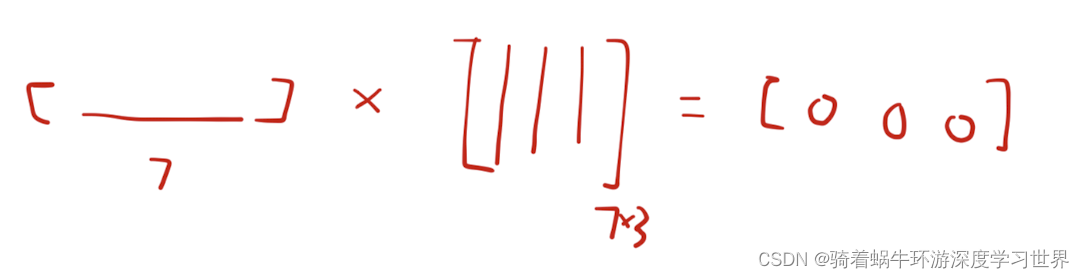
6. 代码示例如下：
  python 复制代码
```
import numpy as np

c = np.array([[1, 0, 0, 0, 0, 0, 0]])  # [1,7]
W = np.random.randn(7, 3)  # [7,3]
# If both a and b are 2-D arrays, it is matrix multiplication
h = np.dot(c, W)  # [1,3]
print(h)
pass
```
7. 本书中还提供了一个MatMul 层，我们详细看一下其中的内容（因为后面也会用到）

2.1 MatMul 层的实现

主要实现一个矩阵相乘的计算，同时提供了反向传播的计算函数

关于矩阵求梯度的理解可以看：【深度学习】7-矩阵乘法运算的反向传播求梯度_矩阵梯度公式-CSDN博客；

初始化：
1. 与输入相乘的是权重；权重就是反向传播时要优化的参数；因此将权重w保存为参数params；
2. 对权重求梯度，由于这里权重是矩阵，因此需要对矩阵中每个元素都计算一个梯度；因此梯度grads是一个与权重w维度相同的矩阵；
python 复制代码
```
def __init__(self, W):
    self.params = [W]
    self.grads = [np.zeros_like(W)] # 放到列表中
    self.x = None
```
前向计算：
1. 示例中x的维度为[4,2]，w的维度为[2,3]；得到计算结果维度为[4,3]；
python 复制代码
```
def forward(self, x):
    W, = self.params
    out = np.dot(x, W)
    self.x = x
    return out
```

反向传播

一般是求权重矩阵的梯度，因为模型训练的目的是更新权重（or参数）

python 复制代码

def backward(self, dout):
    W, = self.params
    dx = np.dot(dout, W.T) # 求关于输入x的梯度
    dW = np.dot(self.x.T, dout) # 求关于权重矩阵的梯度
    self.grads[0][...] = dW # 权重的梯度保存下来
    return dx

3简单word2vec的实现

3.1 CBOW模型的结构

全称为continuous bag-of-words（CBOW）；是一个神经网络模型
目标（任务）：根据上下文预测目标词的神经网络（"目标词"是指中间的单词，它周围的单词是"上下文"）
通过训练这个神经网络，使其能尽可能地进行正确的预测，从而获得单词的分布式表示

3.1.1神经元视角

模型输入的构建
1. 输入是上下文，对于you say goodbye的这个句子，如果要预测的是say，上下文大小是1，则输入是you和goodbye两个单词
2. 根据前面说的神经网络中单词的表示方法，将这两个单词转换为独热编码
模型的网络结构
1. 输入有两个，因此有两个输入层
2. 有一个中间层以及一个输出层
3. 从输入层到中间层的变换由相同的全连接层（即权重共享）
4. 从中间层到输出层神经元的变换由另一个全连接层
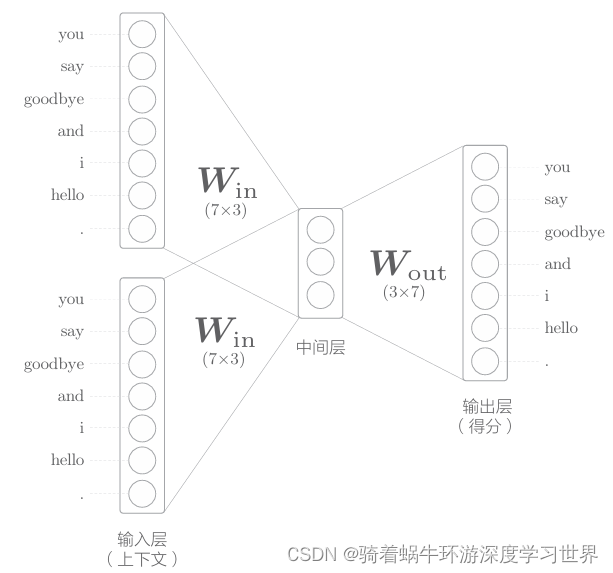
5. 由于输入层有多个，因此，中间层的神经元是各个输入层经全连接层变换后得到的值的"平均"
1. 就上面的例子而言，经全连接层变换后，第1个输入层转化为 h 1 h_1 h1，第2个输入层转化为 h 2 h_2 h2，那么中间层的神经元是 1 2 ( h 1 + h 2 ) \frac{1}{2}(h_1+h_2) 21(h1+h2)；因为两个单词输入维度相同，权重又是一样的，因此 h 1 h_1 h1和 h 2 h_2 h2的维度也是一样的；平均的时候是 h h h中对应位置的元素的平均值；
2. 最后是输出层，包含7个神经元（对应词表里面的7个单词）
  1. 输出层的神经元是各个单词的得分
  2. 对得分应用softmax函数，转换为概率
  3. 得分越大，转换后概率就越大，从而就选择最大的概率对应的单词ID作为预测值
通过神经网络的不断训练，两个权重得到优化；输入层与中间层的这个权重矩阵其实就是单词的分布式表示，我的理解是：
1. 这个矩阵能够把输入的单词映射到一个特征空间，利用映射之后的特征，我们能够对单词是什么进行预测；
2. 我们需要一个能够对每个单词进行表示的向量，合在一起成为一个矩阵，那这个权重矩阵刚刚好
3. 当一个单词进来之后，在权重矩阵的每一列选择对应的值，即可得到高维的特征
注意点：
1. 中间层的神经元数量比输入层少这一点很重要。中间层需要将预测单词所需的信息压缩保存，从而产生密集的向量表示；
2. 输入层的单词的onehot编码只是简单的将单词文字转换为了向量，不包含任何额外的信息，因此需要用另外一个权重矩阵来表示单词更合适
3. 由输入层到中间层，相当于一个编码过程，由中间层到输出层相当于一个解码过程；此时我们再理解一下权重矩阵作为单词的密集向量表示，这个表示其实不是说这个权重矩阵就是代表每个单词，而是一种编码的"工具"，通过它可以区分开每一个单词；

3.1.2层的视角

将之前讲述过的矩阵乘法层应用到这里：由于输入是两个单词，因此输入层使用两个MatMul 层（仍是共享权重），即两个矩阵乘法，两个结果相加再平均，得到中间层的结果；然后再使用一个MatMul 层得到输出

CBOW模型正向计算的代码实现：

python 复制代码

import numpy as np
from utils.Matmul import MatMul

# 样本的上下文单词向量
c0 = np.array([[1, 0, 0, 0, 0, 0, 0]])
c1 = np.array([[0, 0, 1, 0, 0, 0, 0]])

# 权重初始化
w_in = np.random.randn(7, 3)
w_out = np.random.randn(3, 7)

# 构建层
# 权重是待优化的项;这里两个输入层都使用w_in;因此是共享权重的方式
# 但是由于两个输入层都是单独构建了类的实例,因此共享权重会影响参数的更新
in_layer_0 = MatMul(w_in)  # 输入层
in_layer_1 = MatMul(w_in)  # 输入层
out_layer = MatMul(w_out)  # 输出层

# 正向传播（前向计算）
h_0 = in_layer_0.forward(c0)
h_1 = in_layer_1.forward(c1)
h = 0.5 * (h_0 + h_1)
s = out_layer.forward(h)
print('前向计算结果:\n', s)

上述神经网络的输出结果称之为得分；对这个得分施加softmax函数，可以转换为概率分布，选取概率最大的作为对当前位置单词的预测；如果网络具有"良好的权重"，那么在最终得到的概率分布中，正确解将具有最高的概率值

3.1.3多层共享权重时存在的问题

当两个层共享权重时，每个层的梯度更新都会影响另一个层。这可能会导致一些问题，特别是当使用像 Adam 这样的优化器时，因为 Adam 依赖于每个参数的梯度的历史信息来调整学习率。
1. 在 Adam 中，每个参数都有自己的学习率，这个学习率是基于过去的梯度的平方的移动平均值计算的。如果两个层共享权重，那么这两个层的梯度更新就会相互影响，可能导致学习率的计算不准确。
2. 例如，如果一个层的梯度始终很大，而另一个层的梯度始终很小，那么共享的权重的学习率可能会被设置得过大，导致训练不稳定。反之，如果一个层的梯度始终很小，而另一个层的梯度始终很大，那么共享的权重的学习率可能会被设置得过小，导致训练速度过慢。
3. 因此，当两个层共享权重时，使用像 SGD 这样不依赖于每个参数的梯度历史的优化器可能会更稳定。
pytorch中如何解决这种问题：
1. 在 PyTorch 中，如果你有两个层共享权重，你可以通过创建一个层，并在需要的地方多次使用它来实现。这样，当你调用 backward() 方法时，PyTorch 会自动累积这些层的梯度，这样你就可以正确地更新共享的权重了。

以下是一个简单的例子：

python 复制代码

class SharedLayerNet(nn.Module):
    def __init__(self):
        super(SharedLayerNet, self).__init__()
        self.shared_layer = nn.Linear(10, 20)

    def forward(self, x1, x2):
        out1 = self.shared_layer(x1)
        out2 = self.shared_layer(x2)
        return out1, out2

3.2 CBOW模型的学习

即训练上述神经网络，以优化权重，以便能够更准确的进行预测。

学习的结果是，权重w_in(确切地说是w_in和w_out两者)学习到蕴含单词出现模式的向量;

CBOW 模型只是学习语料库中单词的出现模式。++如果语料库不一样，学习到的单词的分布式表示也不一样++。比如，只使用"体育"相关的文章得到的单词的分布式表示，和只使用"音乐"相关的文章得到的单词的分布式表示将有很大不同

但是与先前基于计数的方法相比，他的成本更低

如何学习？目标是什么？
1. 这里是根据上下文对当前位置单词进行预测，预测这个单词是语料库中的哪一个单词，因此本质上是一个多标签分类问题
2. 对于此类问题，可以对模型输出结果施加softmax函数，转换为概率分布，再利用交叉熵损失函数计算这些概率和监督标签之间的交叉熵误差
3. 将此误差作为损失来对神经网络权重进行优化；如下图所示：
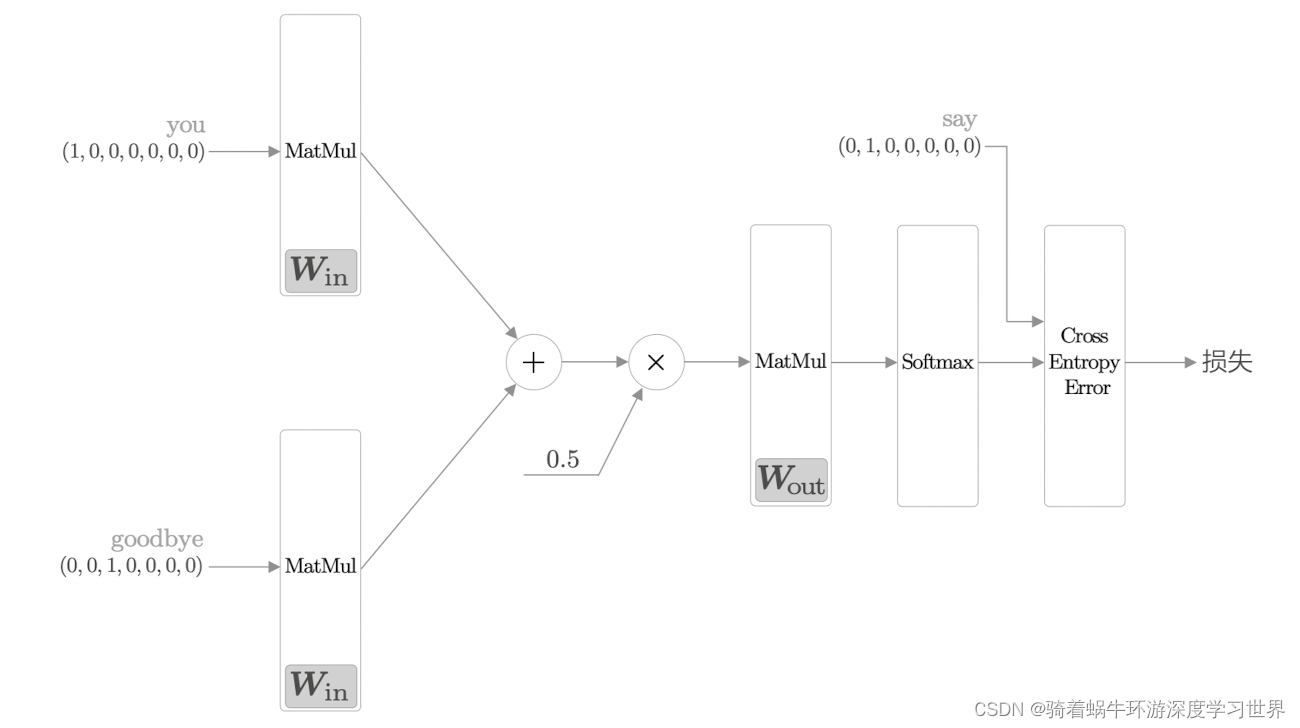
4. 下图为整个过程的维度变化：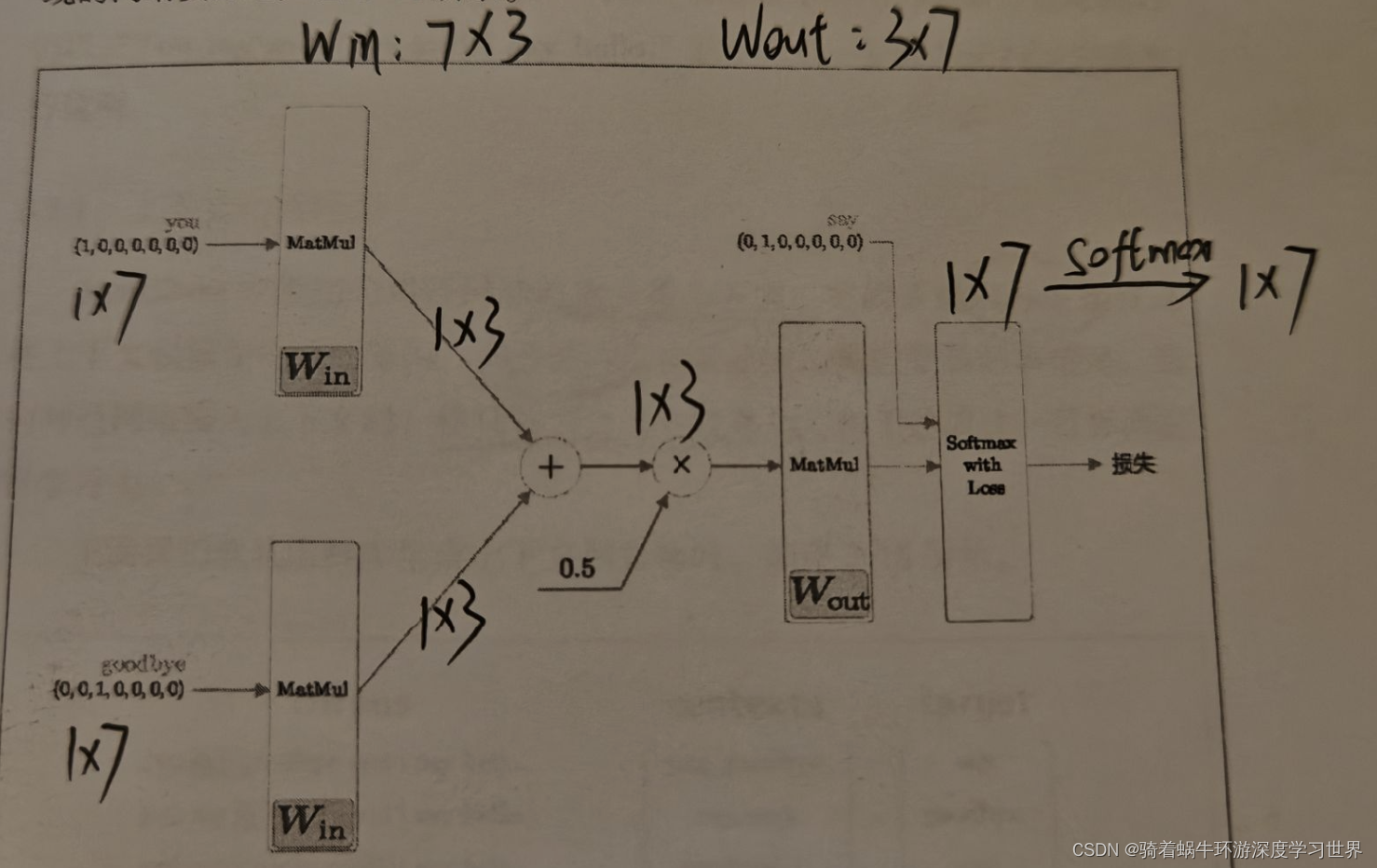

3.3单词的分布式表示

用什么作为单词的分布式表示
1. 用输入层权重w_in：每一行对应于各个单词的分布式表示；维度为[7,3]；
2. 用输出层权重w_out：在列方向上保存了各个单词的分布式表示；维度为[3,7]；
3. 同时使用两个权重；存在多种方式，其中一个方式就是简单地将这两个权重相加
许多研究中也都++仅使用输入侧的++ 权重w_in作为最终的单词的分布式表示
为什么？
1. 简单理解的话
  1. 回想计数方法里面的降维，U矩阵里面每一列相当于一个新的轴；这里也是类似；
  2. 对于输入单词向量[1,7]，这是一个行向量，它与输入层权重w_in的每一列相乘，每一列又刚好是7（与单词个数对应）；每一列都蕴含了一些信息；这里有3列；
  3. 通过乘法，每一列的信息分别作用在输入的单词向量上，将其映射到对应维度上的一个值
2. 深入理解
  1. 书中文献 [38] 通过实验证明了 word2vec 的 skip-gram 模型中w_in的有效性。另外，在与 word2vec 相似的 GloVe[27] 方法中，通过将两个权重相加，也获得了良好的结果；++因此可以看看论文中是如何描述的++；