1.K-Means
假定我们对A、B、C、D四个样品分别测量两个变量，得到的结果见下表。
|--------|--------|--------|
| 样品 | 变量 ||
| 样品 | X1 | X2 |
| A | 5 | 3 |
| B | -1 | 1 |
| C | 1 | -2 |
| D | -3 | -2 |
利用K-Means方法将以上的样品聚成两类。为了实施均值法(K-Means)聚类，首先将这些样品随意分成两类(A、B)和(C、D)。请详细给出每次聚类的中心坐标，计算样品到中心坐标的欧氏平方距离。
解：
第一步: 按要求取K=2，为了实施均值法聚类，我们将这些样品随意分成两类(A、B)和(C、D)，然后计算这两个聚****类的中心坐标(见下表)。中心坐标是通过原始数据计算得来的。
聚类中心坐标一
|-------|----|----|
| 聚类 | 中心坐标 ||
| 聚类 | X1 | X2 |
| （A、B） | 2 | 2 |
| (C、D) | -1 | -2 |
第二步: 计算某个样品到各类中心的欧氏平方距离 ，然后将该样品分配给最近的一类对于样品有变动的类，**重新计算它们的中心坐标，**为下一步聚类做准备。先计算A到两个类的平方距离:
d²(A,(AB))=(5-2)²+(3-2)²=10
d²(A,(CD))= (5 + 1)²+ (3 + 2)²= 61
由于**A到(4、B)的距离小于到(C、D)的距离，因此A不用重新分配。**计算B到两类的平方距离
d²(B,(AB))=(-1-2)²+(1-2)²=10
d²(B,(CD))=(-1 + 1)²+(1 + 2)²=9
由于B到(4、B)的距离大于到(C、D)的距离，因此B要分配给(C、D)类，得到新的聚类是(A)和(B、C、D)。更新中心坐标如下表所示。
聚类中心坐标二
|---------|----|----|
| 聚类 | 中心坐标 ||
| 聚类 | X1 | X2 |
| （A） | 5 | 3 |
| (B、C、D) | -1 | -1 |
第三步:再次检查每个样品，以决定是否需要重新分类。计算各样品到各中心的距离平方，结果如下表所示。
样本到中心的距离平方
|---------|----|----|----|----|
| 聚类 | 样本到中心的距离平方 ||||
| 聚类 | A | B | C | D |
| （A） | 0 | 40 | 41 | 89 |
| (B、C、D) | 52 | 4 | 5 | 5 |
到现在为止，**每个样品都已经分配给距离中心最近的类，聚类过程到此结束。**最终得到K=2的聚类结果是4独自成一类，B、C、D聚成一类。
2.试分析回归与分类的区别。
什么是回归？什么是分类？
分类是找出描述和区分数据类和概念的模型，以便使用模型预测类标号未知的对象类标号。
回归算法是监督型算法的一种，通过利用训练集数据来建立模型，再利用这个模型测试集中的数据进行处理。
区别：
分类和回归都可用于预测，分类的输出是离散的类别值，回归输出的是连续数值。
3.基于正态分布的离群点检测
假设某城市过去10年中7月份的平均温度按递增序排列，结果为24℃、28.9℃、28.9℃、29℃、29.1℃、29.1℃、29.2℃、29.2℃、29.3℃和29.4℃。假定平均温度服从正态分布，由两个参数决定：均值和标准差。假设数据分布在这个区间（以平均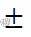
标准差）之外，该数据对象即为离群点。
(1)利用最大似然估计求均值和标准差。
均值（μ）的估计：
其中 n=10，xi 是每个样本的温度值。
将给定的温度值代入公式，得到：
μ=(24+2×28.9+29+2×29.1+2×29.2+29.3+29.4)/10=28.61
标准差（σ）的估计：
由于样本数量 n=10，我们使用样本标准差的无偏估计：
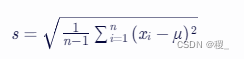
将给定的温度值和计算得到的均值代入公式，得到标准差 s 的值。
s=sqrt([(24-28.61)^2+(28.9-28.61)^2+...+(29.4-28.61)^2]/9)约等于1.63
(2)寻找上述10个对象中的所有离群点。
**根据题目，离群点定义为数据对象落在平均值加减一个标准差之外的值。**即，离群点不在区间
(μ^−σ^,μ^+σ^)=(28.61−1.63,28.61+1.63)=(26.98,30.24) 内。
由于 μ=28.61 和 s≈1.63，我们可以发现所有给定的温度值中**24℃**不在区间 (26.98,30.24) 内。
4.K均值与K中心点
什么是K均值法，什么是K中心点法？
K均值法，每个簇用该簇中对象的均值来表示，为基于质心的的技术。
K中心点法，每个簇用接近簇中心的一个对象来表示，为基于代表对象的技术。
K均值和K中心点算法都可以进行有效的聚类。
(1)概述K均值和K中心点的优缺点。
|-------|------------------------------|----------------------------------------------------|
| | 优点 | 缺点 |
| K均值法 | 聚类时间短。 能对大数据集进行高效划分。 | 必须先指定聚类簇的个数。 只适用于数值属性聚类，对噪声和异常数据很敏感。 不适合发现非凸面形状的簇。 |
| K中心点法 | 对于非凸数据集也能较好聚类效果，且对于噪声点影响比较小 | 算法效率相对K-均值法较低。 有可能出现簇中心点初始化不佳，导致聚类结果不埋想。 |
(2)概述这两种方法与层次聚类方法相比较有何优缺点。
层次聚类方法(AGNES) 对给定数据对象集进行层次的分解，使用距离矩阵作为聚类标准，不需要输入聚类数目K，但需要终止条件。
优点是没有预先设定需要聚类的数量，能够处理复杂的数据结构，相对于K-均值、K-中心点更能反映出数据分布的全貌。
缺点是AGNES算法计算量较大，在大规模数据集上效率较低，且聚类结果可能受到簇合并顺序的影响。
5.Apriori算法：通过限制候选产生发现频繁项集
数据表中有5个事物，设min_sup=60%，min_conf=80%，并有下表所示信息。
|----------|---------------|
| TID | 购买的商品 |
| T100 | {M,O,N,K,E,Y} |
| T200 | {D,O,N,K,E,Y} |
| T300 | {M,A,K,E} |
| T400 | {M,U,C,K,Y} |
| T500 | {C,O,O,K,I,E} |
请用Apriori算法找出频繁项集。
置信度（min_conf）是在找到频繁项集之后，用于生成关联规则时的一个参数，不用理会。
依题得min_sup=0.6*5=3，计算所有单项集的计数得到支持度计数大于等于3的频繁1项集：
m 3
o 3
n 2
k 5
e 4
y 3
d 1
a 1
u 1
c 2
i 1
频繁 1- 顶集: M,O,K,E,Y
然后根据频繁1-项集，找出支持度计数大于等于3的频繁2项集：
mo 1
mk 3
me 2
my 2
ok 3
oe 3
oy 2
ke 4
ky 3
ey 2
频繁 2- 项集: {M,K},{O,K},{O,E} ,{K,Y},{K,E}
再根据频繁2-项集，找出支持度技术大于等于3的频繁3-项集：
oke 3
key 2
频繁 3- 项集: {O,K,E}
故，用Apriori算法找出的频繁项集有频繁 1- 顶集: M,O,K,E,Y; 频繁 2- 项集: {M,K},{O,K},{O,E} ,{K,Y},{K,E}; 频繁 3- 项集: {O,K,E}