堆这种数据结构较为抽象,要想学懂它首先要看一下二叉树的结构是怎么样的,可以点击这个连接看一下。
堆到底有什么用
我们首先要知道堆到底可以干嘛,然后学习它才有方向和动力:
堆可以实现堆排序,它的时间复杂度是NlogN,是和最强的快排是一个档次的,在一些情况下,堆排可能还比快速排序还快一点。
堆的另一个比较厉害的就是POP K 问题。
我们经常会遇到这种问题,比如打王者,我们要看国服前十,世界前100强企业,学校前10名。如果是你会怎么来写这个代码:在很庞大的一个数据里面找出前K个最大的,或者最小的。
或许你学习了快速排序,直接将这些数据排个序,然后输出前面K个不就行了。
但是如果这个数据量足够大,可能有上亿个,而我又规定允许使用的内存是1MB,要怎么做呢?用之前的方法完全是行不通的,只能用堆来解决。
堆的介绍
物理结构和实际结构
在了解堆之前我们要先知道什么是物理结构,什么是实际结构。
物理结构 就是实际要用到那种内存储存形式,是像数组这样连续的,还是像链表这样分散的。实际结构举个例子,二叉树实际结构就是一颗类似树的结构,链表就是类似链状的结构,是我们想象出来直观的。
像顺序表它的物理结构和实际结构都是数组,链表的物理结构和实际结构也是相似的,二叉树也是同理。
但是今天要讲的堆,它的物理结构是数组,但是实际结构却是完全二叉树。是一个比较抽象的数据结构。
堆二者结构的关联
那么我们先要看它的实际结构和物理结构是怎么对应上的。
其中最基本的要求就是,我们看到物理结构的时候,可以将数据全部拆成一颗完全二叉树,而我们看到完全二叉树又能够把它还原成数组。
因为数组的内存是连续的,而我们二叉树通过前中后序遍历始终会有NULL在数据之间的,直接把NULL去掉放进数组里面,我们就无法再通过数组的数据还原成完全二叉树。就算可以,这样也是不直观的。
那么有一个遍历的结果十分直观,而且我们通过遍历的结果结合完全二叉树的特性就可以将二叉树完美的还原出来。那就是层序遍历。
层序遍历的结果就是将值从上到下从左到右把值读一遍
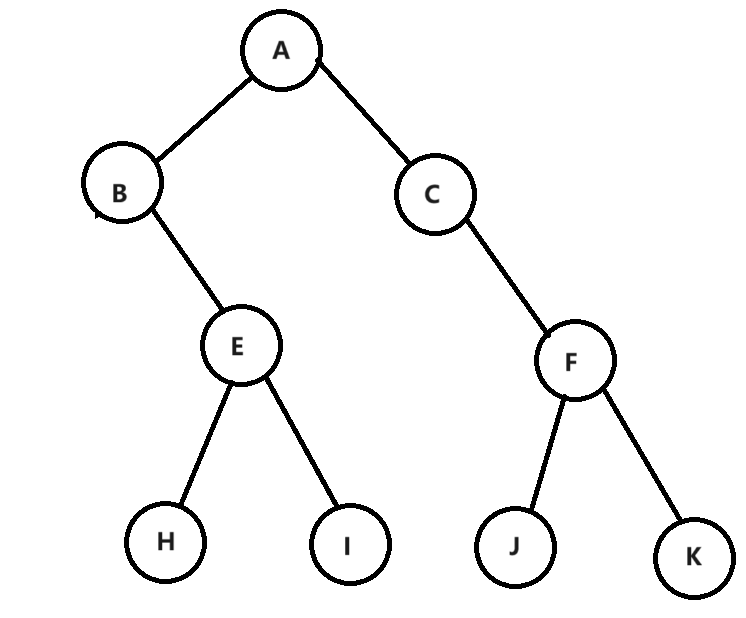
例如这颗树,它的层序遍历结果就输A B C E F H I J K
而下面这颗树就是完全二叉树,它的层序遍历结果就是A B C D E F H I
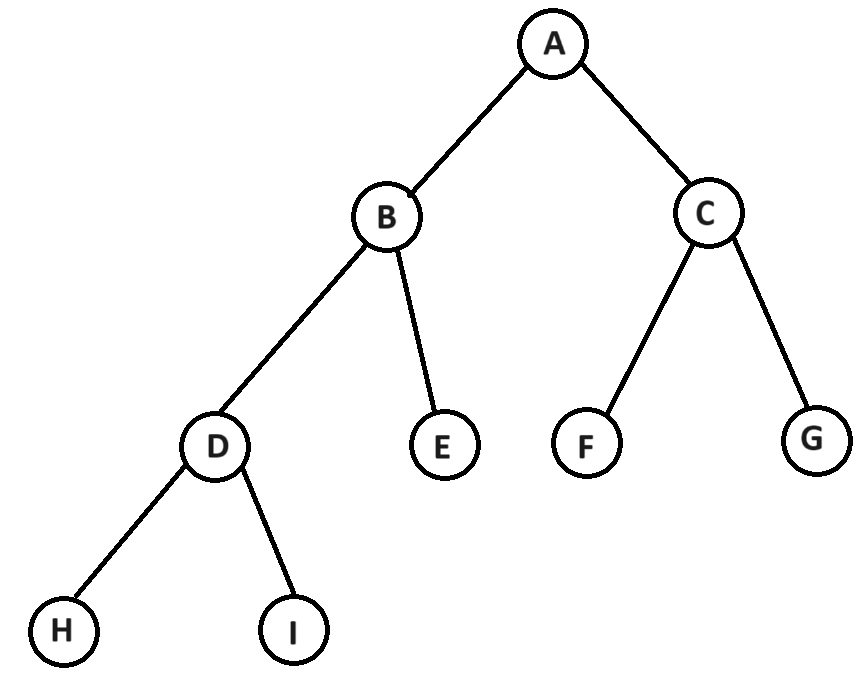
那么层序的结果我们就可以直接写到一个数组里面,那么这个结构就是堆的结构了。
例如我们写一个堆为:1 4 2 5 65 2
那么它的二叉树实际结构就是
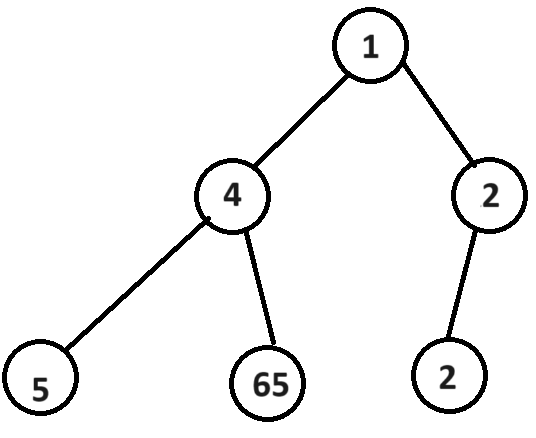
堆的性质
我们知道数组和完全二叉树的关联了,但是如果我单看数组里面的两个数组,怎么知道他们是不是父子关系呢?
例如上面的1 4 2 5 65 2 这里面的4 和 5 有关系吗?
有一个结论,我们父亲节点和子节点之间的关系可以对应数组里面的下标关系:
父亲节点下标*2+1=左节点下标,父亲节点下标*2+2=又孩子节点下标。
翻过来(左孩子节点下标-1)/2=父亲节点下标,(右孩子节点下标-2)/2=父亲节点下标
根据除法有整除的性质,我们可以将这两个化简为:(孩子下标-1)/2=父亲节点下标
大堆小堆
大堆就是实际结构中,父亲节点总是比它的两个孩子节点大。
小堆就是实际结构中,父亲节点总是比它的两个孩子节点小。
那么就有堆顶的数据是最大的或者最小的
建堆(向上调整算法)
我们知道了这两个堆,那么我们如何将普通的堆变成我们的大小堆呢?
首先我们要知道:我们往堆里面push数据是push到数组的末尾的,肯定不是随便插入或者头插,数组内存的整体移动是很耗时的。
如果这个堆里面只有一个数据,那么肯定就是一个大堆或者小堆,但是我们随着下一个数据尾插进去,那么就不会是大堆或者小堆了,那么我们只要每次将尾插的数据进行一个调整,就能保证整体全局都是大堆或者小堆。那么这里就会有一个向上调整算法
代码实现
下面我就以建大堆为例:
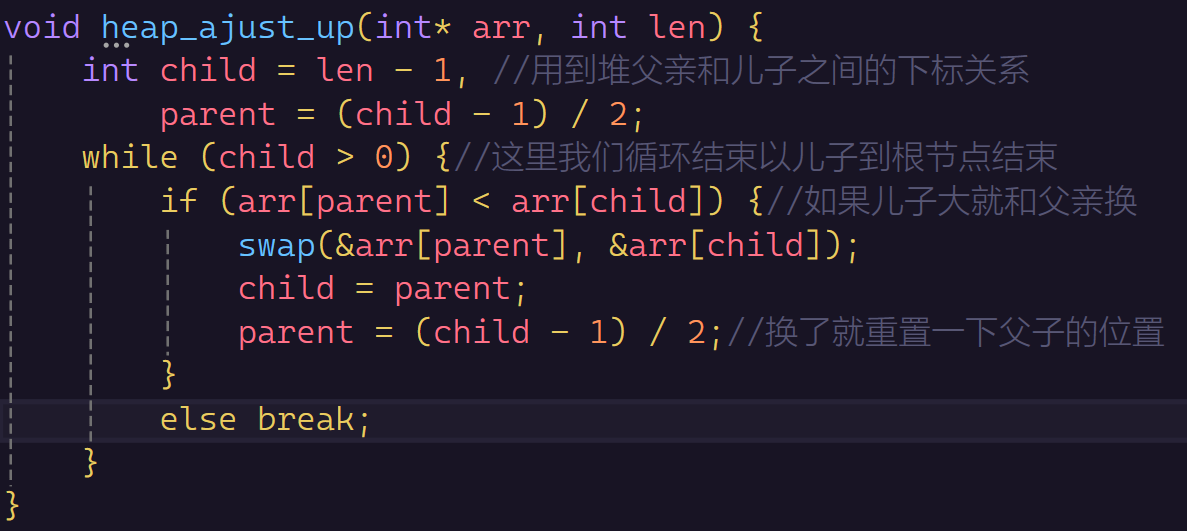
时间复杂度
数据只是在一层一层的进行操作,最大层数是logn,所以是logn的时间复杂度
我们
来看个代码运行情况
首先我们用顺序表/栈来模拟一下堆,这里我用栈模拟一下,顺序表也是一样的,大差不差。提示一下下面有些操作栈里面不能有,不要学,我是懒得找顺序表的代码了用栈平替一下。


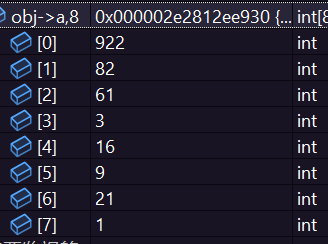
调试完我们发现确实是一个大堆
pop数据(向下调整算法)
我们看一下怎么出数据,和删除数据。出数据好说,我们肯定出堆顶的数据,它是最大或者最小的那一个,肯定TOP一下它。
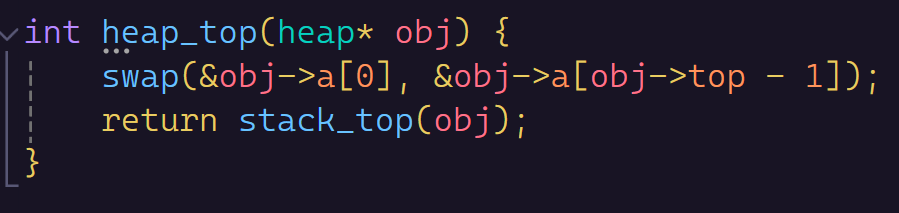
我们只要交换一下末尾的数据和最开始的数据,然后直接TOP,(当然栈这样搞是不行的,栈的数据不能随便动,只能一个一个top,我这里懒得写顺序表的函数了,用栈凑合一下)
如果是顺序表也是这个操作,但是顺序表是允许数据交换的,栈是不可以的。
我们完成这个操作后,本质上堆就少了一个数据了,就是最后一个TOP的数据。那么前面的数据已经不是堆了,我们将原先堆的最后一个数据换到了前面,导致这个堆不成的原因就是这个数据,所以我们只要调整一下这个数据就能再次形成新的堆。
那么就引出了
向下调整算法
向下调整算法有一个不一样的点,就是父亲有两个孩子,是和左孩子换还是和右孩子换呢?
我们要先比较一下,两个孩子哪个大哪个小就行了。
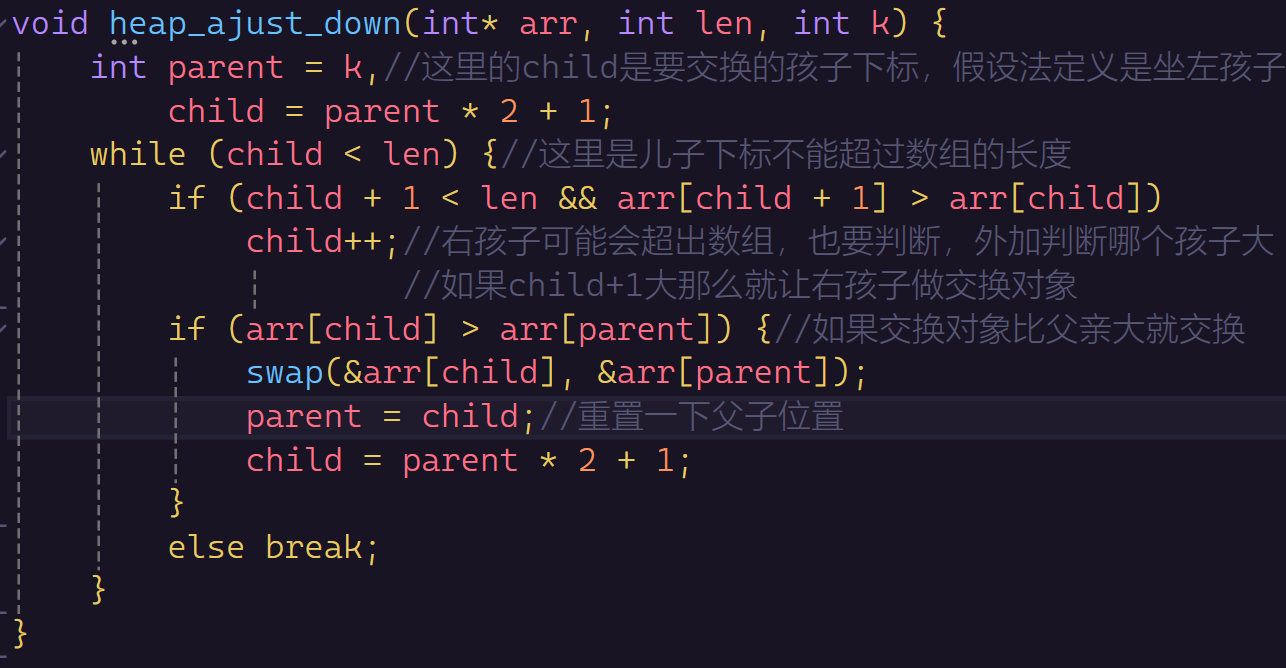
时间复杂度
如果我们是从堆顶来看就是和向上调整算法一样的logn,如果不是从堆顶开始的,那么另说。
这里向下调整算法多一个参数是后面有用的。
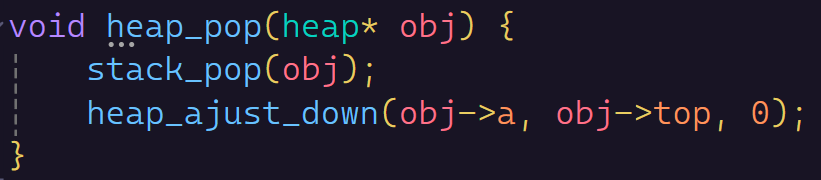
这里的话当然是从堆顶开始向下调整。
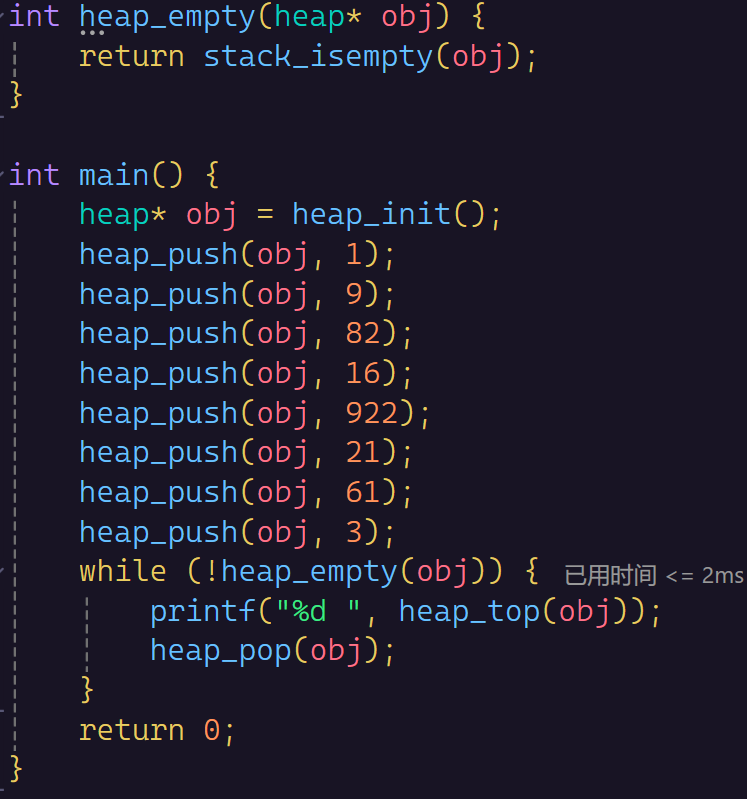
那么通过这一个代码,就可以完成简单的堆的操作

我们就依次将最大的给TOP出来了。已经有排序的感觉了
堆排
那么就到了我们的堆排序:
堆排代码实现
我们在进行TOP的时候,是将最大的数据先和最后一个和数据进行交换,然后在缩短堆的长度,
但是实际我们最大的还是在最后面。我们如果一直重复这个操作,那么每次最大的都回在最后。
什么意思呢,看一看下面的就知道了
我们再来调试一下上面的代码
我们跳转到代码运行完的时候:
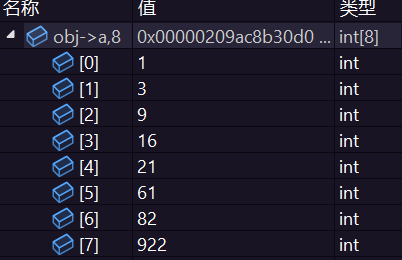
是不是打开了新世界的大门。
那么代码就好写了:我们只要向上向下调整算法就行:
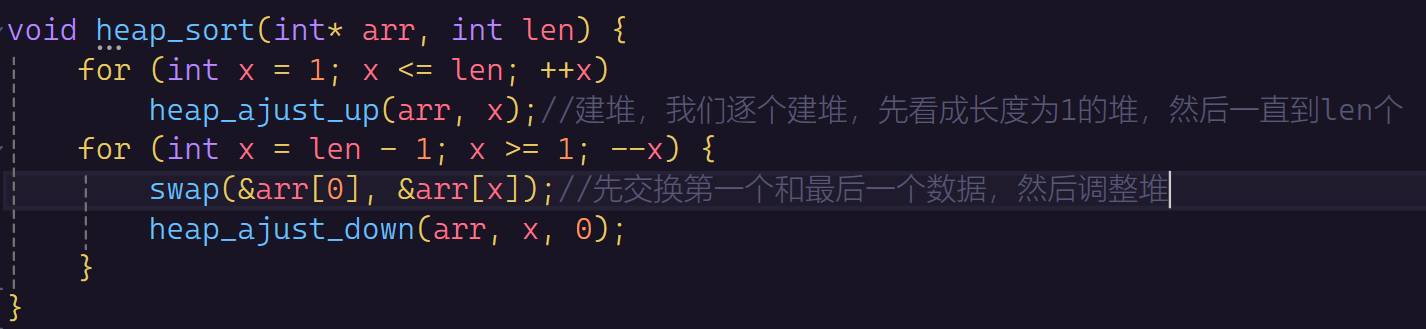
然后我们测试一下
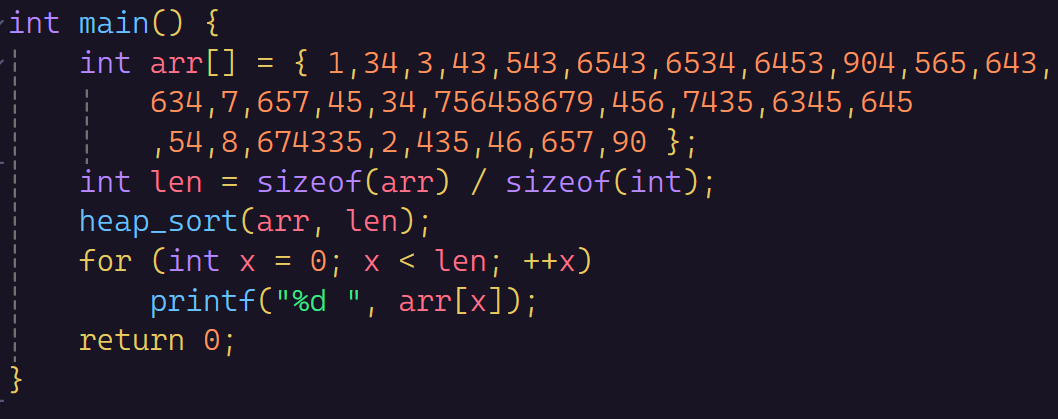

也是没有问题
堆排时间复杂度
每次建堆是n*logn,交换数据向下调整是nlogn,所以总体是NlogN
堆排序优化
我们可以优化建堆过程:
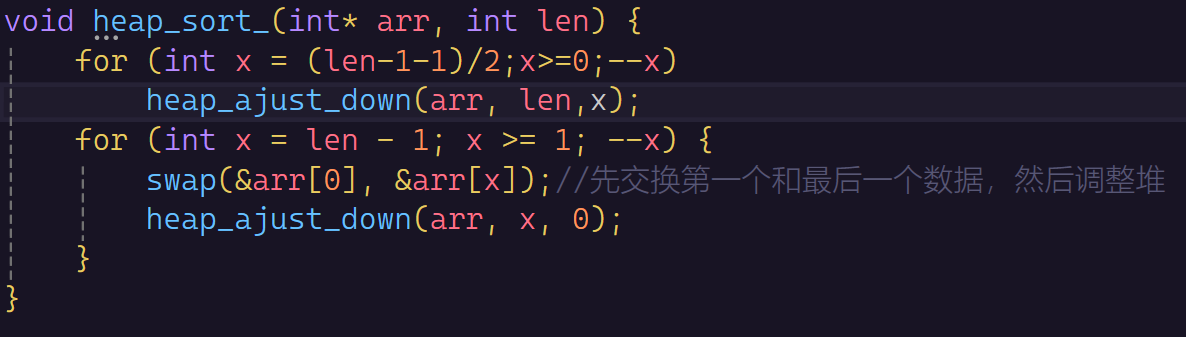
时间复杂度优化后
建堆会变成N,这个分析自行计算,稍微有点复杂
TOP K问题
到了以后一个问题
首先我们在文件里面创建一千万个随机数
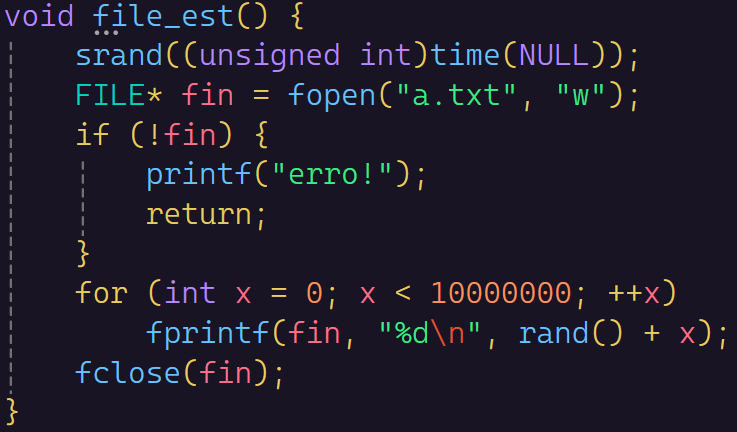
也是十分的随机,这个rand函数是有局限性的,最大的随机数只能到3w多,加个x也只能到1003w多,所以我们再改K个数据以亿为单位的
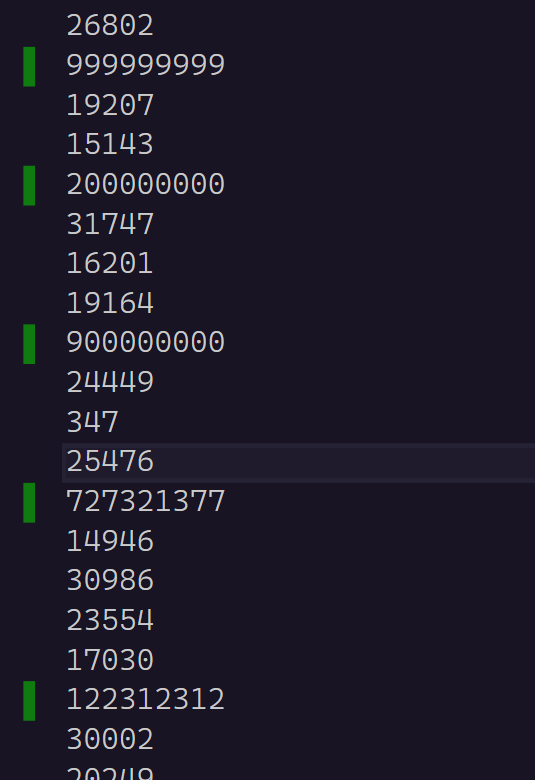
改了5个数,如果等会top最大5个数是这5个就是成功了
那么我们要怎么完成这个问题呢?
就是建一个长度为K的小堆,堆顶就是这K个数最小的,如果比这个还小,就不要入堆了。如果是就入堆,然后把堆顶的数据去除掉就行了。
(这里的上下调整算法都是建小堆的)
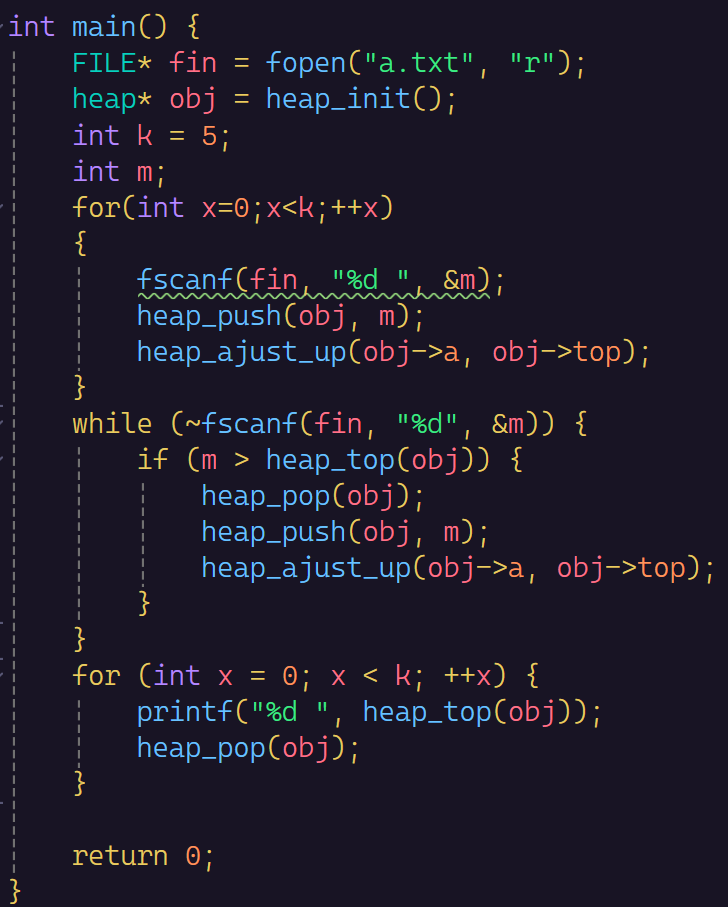

也是成功了
看到这里了点个赞
关注一下吧😁