
与线性规划的本质区别在于决策变量是否取整。
(1)分支定界法
若不考虑整数限制先求出相应松弛问题的最优解:
若松弛问题(线性规划)无解,则ILP(整数规划)无解。
若求得的松弛问题最优解符合整数要求,则是ILP的最优解;
若不满足整数条件,则任选一个不满足整数条件的变量Xi来构造新的约束添加到松弛问题中形成两个子问题:增加两个约束条件:决策变量 <= 决策变量向下取整,决策变量大于 >= 决策变量向下取整 + 1.
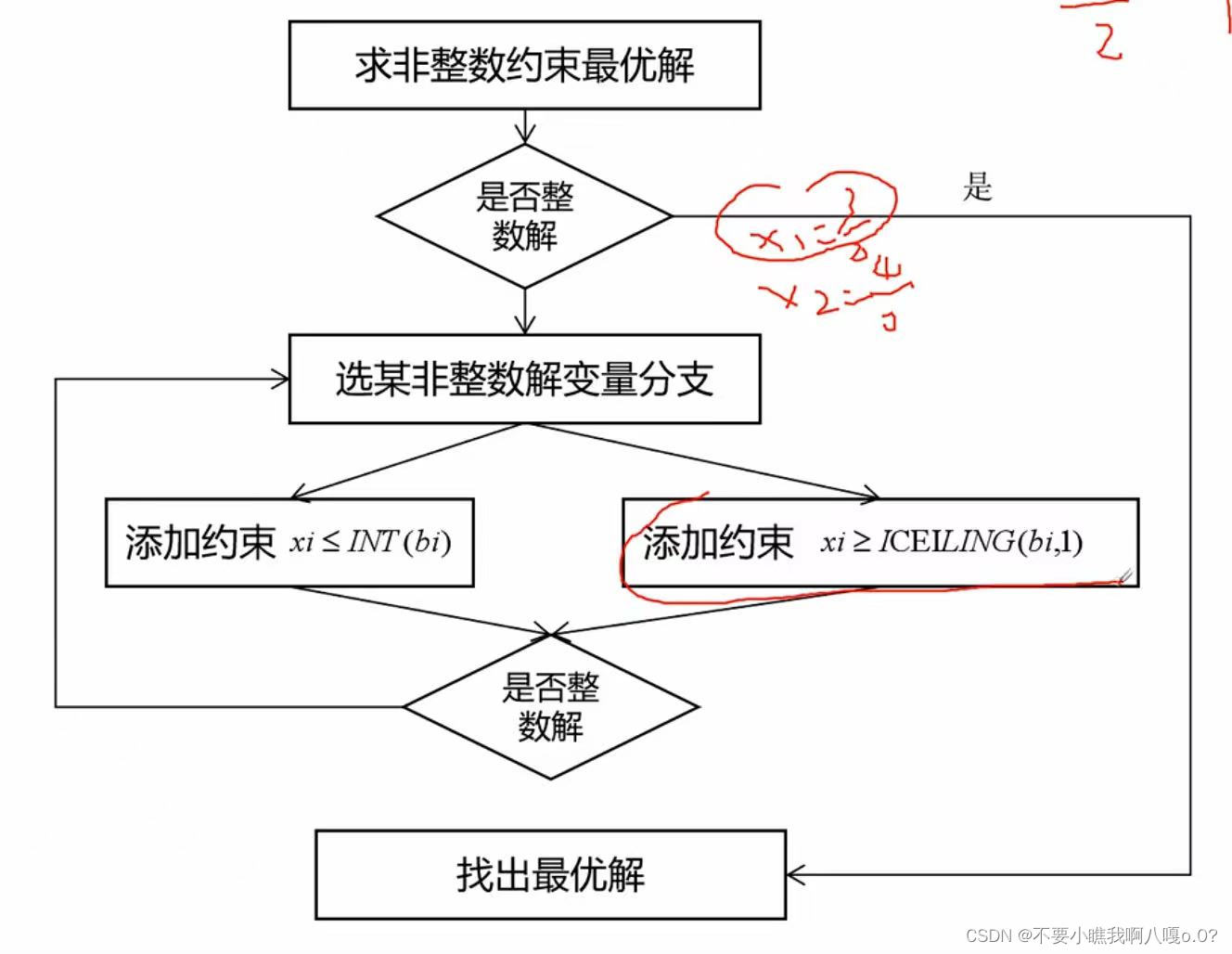
intprog函数:
在linprog函数基础上改造,增加了一个误差e,I为整数约束 :
[x,favl,status] = intprog(f,A,b,I,Aeq,beq,lb,ub,e)status:判断是否有解:
大于0表示有解,小于0表示无解
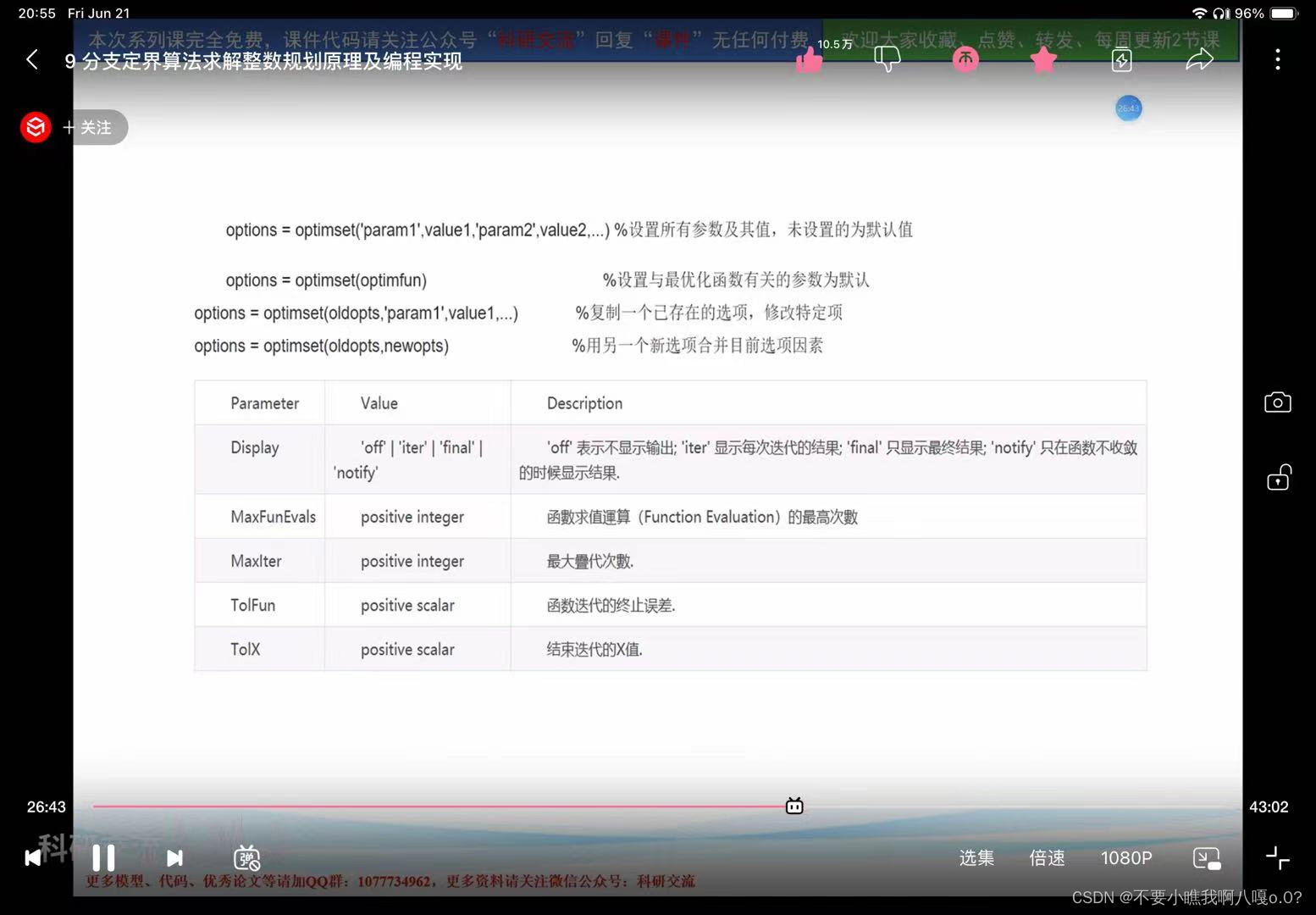
Display选项的可能值:
'off': 不显示任何输出信息。'none': 不显示任何输出信息(与'off'相同)。'final': 仅在求解完成后显示最终结果的信息。'iter': 在每次迭代时显示详细的输出信息,包括迭代次数、当前解、当前目标函数值等。
linprog函数:
[x, fval, exitflag, output] = linprog(f, A, b, Aeq, beq, lb, ub, x0, options)参数解释如下:
f:目标函数的系数向量。A:不等式约束矩阵(左侧)。b:不等式约束向量(右侧)。Aeq:等式约束矩阵(左侧)。beq:等式约束向量(右侧)。lb:变量下界。ub:变量上界。x0:初始点(起始值)。options:优化选项结构体,由optimoptions函数创建。