“文本比对基础：最短编辑距离算法的原理与实现“

最短编辑距离

给定两个字符串 𝐴 和 𝐵，现在要将 𝐴 经过若干操作变为 𝐵，可进行的操作有：

删除--将字符串 𝐴 中的某个字符删除。
插入--在字符串 𝐴 的某个位置插入某个字符。
替换--将字符串 𝐴 中的某个字符替换为另一个字符。

现在请你求出，将 𝐴 变为 𝐵 至少需要进行多少次操作。

输入格式

第一行包含整数 𝑛，表示字符串 𝐴 的长度。

第二行包含一个长度为 𝑛 的字符串 𝐴。

第三行包含整数 𝑚，表示字符串 𝐵 的长度。

第四行包含一个长度为 𝑚 的字符串 𝐵。

字符串中均只包含大小写字母。

输出格式

输出一个整数，表示最少操作次数。

数据范围

1≤𝑛,𝑚≤1000

输入样例：

10
AGTCTGACGC
11
AGTAAGTAGGC

输出样例：

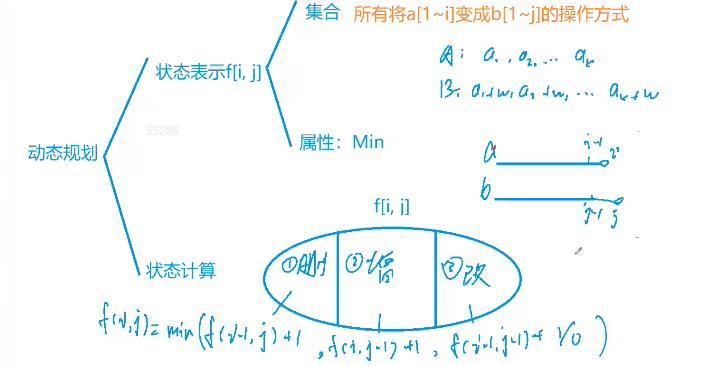
1.状态表示：f[i][j]

集合：将a[1~i] 变成 b[1~j]的操作方式

属性：min

2.状态计算：从最后一步考虑

有三种操作，所以有三个子集

ok子集划分完了

考虑状态转移的时候

先考虑如果我没有进行这个操作应该是什么状态

然后考虑你进行这一步操作之后会对你下一个状态造成什么影响

然后再加上之前状态表示中你决策出来的那个DP属性

这样就可以自然而然地搞出来转移方程啦

1)删除操作：把a[i]删掉之后a[1~i]和b[1~j]匹配

所以之前要先做到a[1~(i-1)]和b[1~j]匹配

f[i-1][j] + 1

2)插入操作：插入之后a[i]与b[j]完全匹配，所以插入的就是b[j]

那填之前a[1~i]和b[1~(j-1)]匹配

f[i][j-1] + 1

3)替换操作：把a[i]改成b[j]之后想要a[1~i]与b[1~j]匹配

那么修改这一位之前，a[1~(i-1)]应该与b[1~(j-1)]匹配

f[i-1][j-1] + 1

但是如果本来a[i]与b[j]这一位上就相等，那么不用改，即

f[i-1][j-1] + 0

好的那么f[i][j]就由以上三个可能状态转移过来，取个min
细节问题：初始化怎么搞

先考虑有哪些初始化嘛

1.你看看在for遍历的时候需要用到的但是你事先没有的

（往往就是什么0啊1啊之类的）就要预处理

2.如果要找min的话别忘了INF

要找有负数的max的话别忘了-INF

ok对应的：

1.f[0][i]如果a初始长度就是0，那么只能用插入操作让它变成b

f[i][0]同样地，如果b的长度是0，那么a只能用删除操作让它变成b

2.f[i][j] = INF //虽说这里没有用到，但是把考虑到的边界都写上还是保险

思路：

用f[i][j]表示第一个字符串的前 i 个字母变为第二个字符串的前 j 个字母所用的最少操作次数。

假设第一个字符串为：AGTCTGACGC

第二个字符串为：AGTAAGTAGGC

f[3][5] 表示把第一个字符串的前三个字母变为第二个字符串的前五个字母所需要的最少操作次数。

也就是把AGT变为AGTAA所用的最少操作次数。

分析递推方程：

把第一个字符串的前 i 个字母变为第二个字符串的前 j 个字母，有三种方法：

把第一个字符串的前 i 个字母变为第二个字符串的前 j - 1 个字符，然后在第一个字符串后面增加第二个字符串的第j个字母。

这种情况下，f[i][j] = f[i][j - 1] + 1。

例如：把AGT变为AGTAA，可以先把AGT变为AGTA，然后再在最后面添加一个字符A。
把第一个字符串的前 i - 1 个字母变为第二个字符串的前 j 个字符，然后去掉最后一个字符。

例如：把AGT变为AGTAA，可以先把AGT变为AGTAAT，然后再去掉一个字符T。

这种情况下，f[i][j] = f[i - 1][j] + 1。

把第一个字符串的前 i - 1 个字母变为第二个字符串的前 j - 1个字符。变化之后，对比最后一个字符，如果相等，则变换完成，如果不同，把第一个字符串的最后一个字符变为第二个字符串的最后一个字符，

例如：把AGT变为AGTAA，可以先把AGT变为AGTAT，然后再在最后面添加一个字符T变为A。

例如：把AGT变为AGTAT，可以先把AGT变为AGTAT，因为最后一个字符相同，不再做处理。

这种情况下，f[i][j] = f[i - 1][j - 1] + 1(最一个字符不同) 或f[i][j] = f[i - 1][j + 1] (最一个字符相同)。

取三种情况的最小值，就是f[i][j]。

时间复杂度：O(n^2)。

代码：

cpp 复制代码

#include <iostream>
using namespace std;
const int N = 1010;

char a[N], b[N];//分别存放两个字符串
int f[N][N];//存储结果

int n, m;//两个字符串的长度

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i];

    cin >> m;
    for(int i = 1; i <= m; i++) cin >> b[i];
    //边界，a 字符串的前 i 个字符变为 b 字符串的前 0 个字符，需要 i 步
    for(int i = 0; i <= n; i++) f[i][0] = i;
    //边界，a 字符串的前 0 个字符变为 b 字符串的前 i 个字符，需要 i 步
    for(int i = 0; i <= m; i++) f[0][i] = i;
    
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <=m; j++)
        {
            //情况一 二
            f[i][j] = min(f[i][j - 1] + 1, f[i - 1][j] + 1);
            //情况三
            if(a[i] != b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
            else f[i][j] = min(f[i][j], f[i - 1][j - 1]);
        }
    }
    //f[n][m] 表示 a 字符传递额前 n 个字符变为 b 字符传递额前 m 个字符需要的最少步骤。
    cout << f[n][m];

}