【MPC】模型预测控制笔记 (3)：无约束输出反馈MPC

目录

• 前言
• • 输出反馈MPC
  • [将要用到的基础概念 参考：《现代控制理论（第3版） (刘豹,唐万生) 》](#将要用到的基础概念 参考：《现代控制理论（第3版） (刘豹,唐万生) 》)
  • • 【基础】系统能控性
    • 【基础】系统能观性
    • 【基础】能控性和能观性的对偶关系
• 一、观测器设计
• • [1.1 线性观测器设计](#1.1 线性观测器设计)
  • [1.2 误差（稳定性）分析](#1.2 误差（稳定性）分析)
  • [1.3 MATLAB实例](#1.3 MATLAB实例)
  • • [1.3.1 极点配置](#1.3.1 极点配置)
    • [1.3.2 LQR设计最优增益](#1.3.2 LQR设计最优增益)
• 二、无约束输出反馈MPC
• • [2.1 稳定性分析](#2.1 稳定性分析)
  • [2.2 MATLAB实例](#2.2 MATLAB实例)

---

前言

致谢 【模型预测控制（2022春）lecture 3-1 Output feedback MPC】

输出反馈MPC

针对更通用的系统：
x k + 1 = A x k + B u k y k = C x k (1) \begin{align*} x_{k+1} &= Ax_k + Bu_k \\ y_k &= Cx_k \end{align*} \tag{1} xk+1yk=Axk+Buk=Cxk(1)

其中， x k ∈ R n x_k \in \mathbb{R}^n xk∈Rn 是系统的全状态， u k ∈ R p u_k \in \mathbb{R}^p uk∈Rp 是系统的输入， y k ∈ R m y_k \in \mathbb{R}^m yk∈Rm 是可知的系统输出。

当 m < n m<n m<n 时，说明部分状态不可测量，需要增加观测器来观测系统的全状态，此前提是系统是可观测的（能观性）。

由此即可通过系统的输出反馈来设计 MPC 控制器。

将要用到的基础概念 参考：《现代控制理论（第3版） (刘豹,唐万生) 》

【基础】系统能控性

定义 ：若存在连续的输入 u ( t ) u(t) u(t)，可在有限时间 t 0 , t f t_0, \~ t_f t0, tf 内，使系统从状态 x ( t 0 ) x(t_0) x(t0)到达任一终端状态 x ( t f ) x(t_f) x(tf)，则称该状态是能控的。若系统每一状态都能控，则称系统是能观的。

简单理解就是：系统中每个子状态都独立地直接或间接地受输入影响则可控。

【基础】系统能观性

定义 ：若系统在有限观测时间 t f > t 0 t_f > t_0 tf>t0 内，可根据 t 0 , t f t_0, \~ t_f t0, tf 期间输出的 y ( t ) y(t) y(t)，唯一地确定系统状态 x ( t 0 ) x(t_0) x(t0)，则称该状态是能观的。若系统每一状态都能观测，则称系统是能观的。

针对离散系统的简单理解就是：

将系统 k k k 时刻的全状态 x k x_k xk 分为两块，记 x k = x k + ∪ x k − x_k = x_k^+ \cup x_k^- xk=xk+∪xk−，

系统输出 y k y_k yk 可能只与部分的系统状态 x k + x_k^+ xk+ 存在联系，若系统中与 y k y_k yk没有直接关系的状态 x k − x_k^- xk−，其与 x k + x_k^+ xk+ 存在联系，

就可通过有限的多时刻的系统输出 y k , y k + 1 , ⋯ y_k,y_{k+1},\cdots yk,yk+1,⋯，建立足够多的独立方程，求解出系统的全状态 x k x_k xk.

故 x k − x_k^- xk−与 x k + x_k^+ xk+ 是否存在联系决定了系统的能观性。

《现代控制理论（第3版） (刘豹,唐万生) 》中给出了许多系统能控/观性的判定方法。

【基础】能控性和能观性的对偶关系

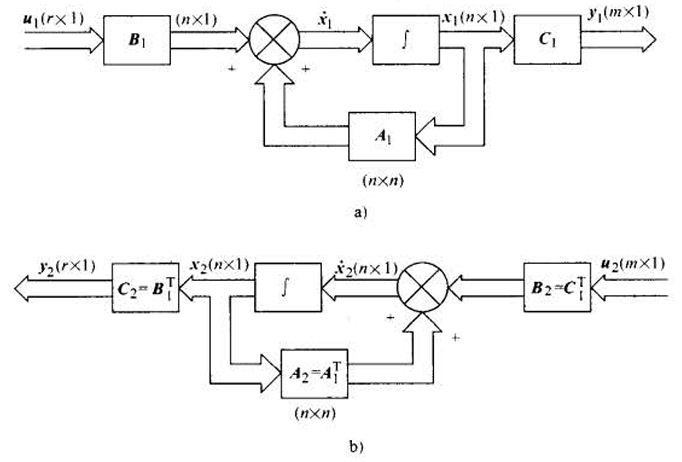
对偶关系定义 ：

系统 ∑ 1 \sum _1 ∑1 ：
x ˙ 1 = A 1 x 1 + B 1 u 1 y ˙ 1 = C 1 x 1 \begin{align*} \dot{x}_1 &= A_1 x_1 + B_1 u_1 \\ \dot{y}_1 &= C_1 x_1 \end{align*} x˙1y˙1=A1x1+B1u1=C1x1

系统 ∑ 2 \sum _2 ∑2 ：
x ˙ 2 = A 2 x 2 + B 2 u 2 y ˙ 2 = C 2 x 2 \begin{align*} \dot{x}_2 &= A_2 x_2 + B_2 u_2 \\ \dot{y}_2 &= C_2 x_2 \end{align*} x˙2y˙2=A2x2+B2u2=C2x2

若：
A 2 = A 1 T , B 2 = C 1 T , C 2 = B 1 T A_2 = A_1^T, \quad B_2 = C_1^T, \quad C_2 = B_1^T A2=A1T,B2=C1T,C2=B1T

则称系统 ∑ 1 \sum _1 ∑1 和 ∑ 2 \sum _2 ∑2 是互为对偶的。

对偶原理 ：

系统 ∑ 1 \sum _1 ∑1 和 ∑ 2 \sum _2 ∑2 是互为对偶，则 ∑ 1 \sum _1 ∑1 的能控性等价于 ∑ 2 \sum _2 ∑2 的能观性， ∑ 1 \sum _1 ∑1 的能观性等价于 ∑ 2 \sum _2 ∑2 的能控性。

应用 ：

在设计观测器的观测增益 L L L 时，可通过对偶的控制系统，使用控制器设计方法设计最优反馈增益 K K K，有 L = K T L = K^T L=KT.

---

一、观测器设计

1.1 线性观测器设计

针对系统 (1)，设 k k k 时刻观测的状态为 x ^ k \hat{x}{k} x^k，线性观测器可设计为：
x ^ k + 1 = A x ^ k + B u k + H ( y k − C x ^ k ) (2) \hat{x}{k+1} = A\hat{x}{k} + Bu_k + H(y_k - C\hat{x}{k}) \tag{2} x^k+1=Ax^k+Buk+H(yk−Cx^k)(2)

上式可称为 观测器状态方程，其中 H H H 为观测增益.

1.2 误差（稳定性）分析

定义误差为 x ~ k = x k − x ^ k \tilde{x}k = x_k - \hat{x}{k} x~k=xk−x^k，由系统状态方程-观测器状态方程得：
x ~ k + 1 = A x ~ k − L ( y k − C x ^ k ) \tilde{x}_{k+1} = A\tilde{x}k - L(y_k - C\hat{x}{k}) x~k+1=Ax~k−L(yk−Cx^k)

将输出方程代入上式可整理得：
x ~ k + 1 = ( A − L C ) x ~ k (3) \tilde{x}_{k+1} = (A-LC)\tilde{x}_k \tag{3} x~k+1=(A−LC)x~k(3)

由李雅普诺夫稳定性间接法可知，当 ∣ e i g ( A − L C ) ∣ < 1 |\mathrm{eig}(A-LC)|<1 ∣eig(A−LC)∣<1 时，误差将趋于 0.

L L L 可通过其对偶系统来设计。

式 (3) 可以写为： x ~ k + 1 = A ′ x ~ k \tilde{x}_{k+1} = A^\prime \tilde{x}_k x~k+1=A′x~k，其中 A ′ = ( A − L C ) A^\prime = (A-LC) A′=(A−LC).

对偶系统为
x ~ k + 1 = ( A − L C ) T x ~ k ⇒ x ~ k + 1 = A T x ~ k − C T L T x ~ k \begin{align*} \tilde{x}_{k+1} &= (A-LC)^T \tilde{x}k\\ \Rightarrow \tilde{x}{k+1} &= A^T\tilde{x}_k - C^T L^T \tilde{x}_k \end{align*} x~k+1⇒x~k+1=(A−LC)Tx~k=ATx~k−CTLTx~k

以上形式就转为了我们熟悉的线性反馈控制系统的形式： x k + 1 = A x k − B K x k x_{k+1} = Ax_k - BKx_k xk+1=Axk−BKxk.

我们可用极点配置或最优控制来设计增益使系统渐近稳定.

因为 e i g ( A ′ ) = e i g ( ( A ′ ) T ) \mathrm{eig}(A^\prime) = \mathrm{eig}((A^\prime)^T) eig(A′)=eig((A′)T)，所以当控制系统渐近稳定，观测器误差也将收敛为0.

1.3 MATLAB实例

针对式 (2) 形式的观测器，需要使式 (3) 系统的状态稳定为 0 \mathbf{0} 0.

设系统中 A = 1.1 2 0 0.95 A = \begin{bmatrix} 1.1 & 2 \\ 0 & 0.95 \end{bmatrix} A=1.1020.95， B = 0 0.079 B = \begin{bmatrix} 0 \\ 0.079 \end{bmatrix} B=00.079， C = 1 0 C = \begin{bmatrix} 1 & 0 \end{bmatrix} C=10.

设计观测增益 L L L，使 ∣ e i g ( A − L C ) ∣ < 1 |\mathrm{eig}(A-LC)|<1 ∣eig(A−LC)∣<1，即可使观测器误差收敛为0.

下面将根据对偶原理，使用极点配置法和基于对偶原理的LQR方法来设计.

式 (3) 的对偶系统为：
x ~ k + 1 = A T x ~ k − C T L T x ~ k \tilde{x}_{k+1} = A^T\tilde{x}_k - C^T L^T \tilde{x}_k x~k+1=ATx~k−CTLTx~k

对应控制系统：
x ~ k + 1 ′ = A ′ x ~ k ′ − B ′ K ′ x ~ k ′ \tilde{x}_{k+1}^\prime = A^\prime\tilde{x}_k^\prime - B^\prime K^\prime \tilde{x}_k^\prime x~k+1′=A′x~k′−B′K′x~k′

其中 A ′ = A T A^\prime = A^T A′=AT， B ′ = C T B^\prime = C^T B′=CT， K ′ = L T K^\prime = L^T K′=LT.

1.3.1 极点配置

A = [1.1 2;0 0.95];
B = [0; 0.079];
C = [1, 0];

Ap = A';
Bp = C';

%% 极点配置
p = [0.5 + 0.5j, 0.5 - 0.5j]; % 适当选取极点
K = place(Ap, Bp, p);

L = K';
disp(eig(A - L*C))
disp(abs(eig(A - L*C)))

得 L = 1.0500 0.2263 L = \begin{bmatrix} 1.0500 \\ 0.2263 \end{bmatrix} L=1.05000.2263.

1.3.2 LQR设计最优增益

LQR相关内容可参考 离散LQR原理 .

A = [1.1 2;0 0.95];
B = [0; 0.079];
C = [1, 0];

Ap = A';
Bp = C';

%% LQR 最优增益
K = LQR(Ap, Bp, eye(2), 0.1, 500, 1e-6);
L = K';
disp(eig(A - L*C))
disp(abs(eig(A - L*C)))
%%
function K = LQR(A, B, Q, R, maxIter, eps)
% A、B分别为系统矩阵和输入矩阵，Q和R分别为状态误差和输入的对角权重矩阵
% maxIter为最大迭代步数N，eps为迭代精度C
	i = 1; P = Q; delta = 1e9;
	while i < maxIter && delta > eps
	    Pn = Q + A' * (P - P*B* inv(R+B'*P*B) *B'*P) * A;
	    delta = max(abs(Pn-P), [], "all");
	    P = Pn;
	    i = i+1;
	end
	K = inv(R + B' * P * B) * B' * P * A;
end

得 L = 1.8342 0.3571 L = \begin{bmatrix} 1.8342 \\ 0.3571 \end{bmatrix} L=1.83420.3571.

二、无约束输出反馈MPC

针对系统：
x k + 1 = A x k + B u k y k = C x k \begin{align*} x_{k+1} &= Ax_k + Bu_k \\ y_k &= Cx_k \end{align*} xk+1yk=Axk+Buk=Cxk

由 【MPC】模型预测控制笔记 (1)：无约束MPC 可知，

无约束MPC的输入可写为状态反馈形式：
u k = − K x k u_k = -Kx_k uk=−Kxk

其中 K = I p × p 0 0 ⋯ 0 ( H T Q ′ H + R ′ ) − 1 H T Q ′ G K = I_{p\\times p} \~0 \~0 \~\\cdots \~0(\mathcal{H}^T \mathcal{Q}^\prime \mathcal{H} + \mathcal{R}^\prime)^{-1}\mathcal{H}^T \mathcal{Q}^\prime \mathcal{G} K=Ip×p 0 0 ⋯ 0(HTQ′H+R′)−1HTQ′G.

无约束输出反馈MPC可直接使用观测器观测状态代替真实状态：
u k = − K x ^ k u_k = -K\hat{x}_k uk=−Kx^k

其中 x ^ k + 1 = A x ^ k + B u k + L ( y k − C x ^ k ) \hat{x}{k+1} = A\hat{x}{k} + Bu_k + L(y_k - C\hat{x}_{k}) x^k+1=Ax^k+Buk+L(yk−Cx^k)，记观测误差为 x ~ k = x k − x ^ k \tilde{x}k = x_k - \hat{x}{k} x~k=xk−x^k.

系统可改写为：
x k + 1 = A x k − B K x ^ k = A x k − B K ( x k − x ~ k ) (4) \begin{align*} x_{k+1} &= Ax_k - BK\hat{x}_k \\ &= Ax_k - BK(x_k - \tilde{x}_k) \end{align*} \tag{4} xk+1=Axk−BKx^k=Axk−BK(xk−x~k)(4)

观测误差可写为：
x ~ k + 1 = ( A − L C ) x ~ k (5) \tilde{x}_{k+1} = (A-LC)\tilde{x}_k \tag{5} x~k+1=(A−LC)x~k(5)

2.1 稳定性分析

构建增广系统：

x k + 1 x \~ k + 1 \] = \[ A − B K B K 0 A − L C \] \[ x k x \~ k \] \\begin{align\*} \\begin{bmatrix} x_{k+1} \\\\ \\tilde{x}_{k+1} \\end{bmatrix} = \\begin{bmatrix} A-BK \& BK \\\\ 0 \& A - LC \\end{bmatrix} \\begin{bmatrix} x_{k} \\\\ \\tilde{x}_{k} \\end{bmatrix} \\end{align\*} \[xk+1x\~k+1\]=\[A−BK0BKA−LC\]\[xkx\~k

系统的的稳定性取决于
A a u g = A − B K B K 0 A − L C \begin{align*} A_{aug} = \begin{bmatrix} A-BK & BK \\ 0 & A - LC \end{bmatrix} \end{align*} Aaug=A−BK0BKA−LC 的特征值。

当 ∣ e i g ( A a u g ) ∣ < 1 |\mathrm{eig}(A_{aug})|<1 ∣eig(Aaug)∣<1 时，系统渐近稳定，其中 e i g ( A a u g ) = e i g ( A − B K ) ∪ e i g ( A − L C ) \mathrm{eig}(A_{aug}) = \mathrm{eig}(A-BK) \cup \mathrm{eig}(A-LC) eig(Aaug)=eig(A−BK)∪eig(A−LC).

由此可见，整体系统的稳定性取决了控制器和观测器，这两部分可独立设计，

但需要注意的时，观测器应收敛得比控制器更快，否则，控制器会根据不准确的观测结果将系统控歪。

线性代数基础：三角分块矩阵的特征值为其对角子块上的特征值集合。

证明：

首先证明三角分块矩阵的行列式等于其对角子块行列式的乘积（参考：分块矩阵行列式的性质证明）：
性质1：从一行（列）中减去另一行（列）的倍数，行列式保持不变．
性质2：三角矩阵的行列式为其主对角线上元素的乘积．
参考：《线性代数导论：第五版 (（美）Gilbert Strang著 海昕, 文军, 屈龙江, 钱旭译) 》

设
∣ D ∣ = ∣ a 11 ⋯ a 1 k ⋮ ⋮ 0 a k 1 ⋯ a k k c 11 ⋯ c 1 k b 11 ⋯ b 1 n ⋮ ⋮ ⋮ ⋮ c n 1 ⋯ c n k b n 1 ⋯ b n n ∣ , ∣ D 1 ∣ = ∣ a 11 ⋯ a 1 k ⋮ ⋮ a k 1 ⋯ a k k ∣ , ∣ D 2 ∣ = ∣ b 11 ⋯ b 1 n ⋮ ⋮ b n 1 ⋯ b n n ∣ \begin{align*} &|D| = \begin{vmatrix} a_{11} & \cdots & a_{1k} & & & \\ \vdots & & \vdots & & 0 & \\ a_{k1} & \cdots & a_{kk} & & & \\ c_{11} & \cdots & c_{1k} & b_{11} & \cdots & b_{1n} \\ \vdots & & \vdots & \vdots & & \vdots \\ c_{n1} & \cdots & c_{nk} & b_{n1} & \cdots & b_{nn} \end{vmatrix}, &|D_{1}| = \begin{vmatrix} a_{11} & \cdots & a_{1k} \\ \vdots & & \vdots \\ a_{k1} & \cdots & a_{kk} \end{vmatrix}, &|D_{2}| = \begin{vmatrix} b_{11} & \cdots & b_{1n} \\ \vdots & & \vdots \\ b_{n1} & \cdots & b_{nn} \end{vmatrix} \end{align*} ∣D∣= a11⋮ak1c11⋮cn1⋯⋯⋯⋯a1k⋮akkc1k⋮cnkb11⋮bn10⋯⋯b1n⋮bnn ,∣D1∣= a11⋮ak1⋯⋯a1k⋮akk ,∣D2∣= b11⋮bn1⋯⋯b1n⋮bnn

分别通过行变换和列变换可得：
∣ D 1 ∣ = ∣ p 11 ⋯ 0 ⋮ ⋱ ⋮ p k 1 ⋯ p k k ∣ = p 11 p 22 ⋯ p k k , ∣ D 2 ∣ = ∣ q 11 ⋯ 0 ⋮ ⋱ ⋮ q n 1 ⋯ q n n ∣ = p 11 p 22 ⋯ p n n \begin{align*} &|D_{1}| = \begin{vmatrix} p_{11} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ p_{k1} & \cdots & p_{kk} \end{vmatrix} = \mathrm{p}{11} \mathrm{p}{22} \cdots \mathrm{p}{\mathrm{kk}}, &|D{2}| = \begin{vmatrix} q_{11} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ q_{n1} & \cdots & q_{nn} \end{vmatrix} = \mathrm{p}{11} \mathrm{p}{22} \cdots \mathrm{p}_{\mathrm{nn}} \end{align*} ∣D1∣= p11⋮pk1⋯⋱⋯0⋮pkk =p11p22⋯pkk,∣D2∣= q11⋮qn1⋯⋱⋯0⋮qnn =p11p22⋯pnn

有：
∣ D ∣ = ∣ p 11 ⋯ 0 ⋮ ⋮ 0 p k 1 ⋯ p k k c 11 ⋯ c 1 k q 11 ⋯ 0 ⋮ ⋮ ⋮ ⋮ c n 1 ⋯ c n k q n 1 ⋯ q n n ∣ = p 11 p 22 ⋯ p k k ⋅ p 11 p 22 ⋯ p n n = ∣ D 1 ∣ ∣ D 2 ∣ \begin{align*} |D| = \begin{vmatrix} p_{11} & \cdots & 0 & & & \\ \vdots & & \vdots & & 0 & \\ p_{k1} & \cdots & p_{kk} & & & \\ c_{11} & \cdots & c_{1k} & q_{11} & \cdots & 0 \\ \vdots & & \vdots & \vdots & & \vdots \\ c_{n1} & \cdots & c_{nk} & q_{n1} & \cdots & q_{nn} \end{vmatrix} \end{align*} = \mathrm{p}{11} \mathrm{p}{22} \cdots \mathrm{p}{\mathrm{kk}} \cdot \mathrm{p}{11} \mathrm{p}{22} \cdots \mathrm{p}{\mathrm{nn}} = |D_1||D_2| ∣D∣= p11⋮pk1c11⋮cn1⋯⋯⋯⋯0⋮pkkc1k⋮cnkq11⋮qn10⋯⋯0⋮qnn =p11p22⋯pkk⋅p11p22⋯pnn=∣D1∣∣D2∣

在计算特征值时有：
∣ D − λ I ∣ = ∣ D 1 − λ I ∣ ∣ D 2 − λ I ∣ = 0 |D-\lambda I| = |D_1-\lambda I| |D_2-\lambda I| = 0 ∣D−λI∣=∣D1−λI∣∣D2−λI∣=0

故 三角分块矩阵的特征值为其对角子块上的特征值集合 得证.

2.2 MATLAB实例

针对系统 (1)，设系统中 A = 1.1 2 0 0.95 A = \begin{bmatrix} 1.1 & 2 \\ 0 & 0.95 \end{bmatrix} A=1.1020.95， B = 0 0.079 B = \begin{bmatrix} 0 \\ 0.079 \end{bmatrix} B=00.079， C = 1 0 C = \begin{bmatrix} 1 & 0 \end{bmatrix} C=10.

由 【MPC】模型预测控制笔记 (1)：无约束MPC 可知控制器反馈增益 K = I p × p 0 0 ⋯ 0 ( H T Q ′ H + R ′ ) − 1 H T Q ′ G K = I_{p\\times p} \~0 \~0 \~\\cdots \~0(\mathcal{H}^T \mathcal{Q}^\prime \mathcal{H} + \mathcal{R}^\prime)^{-1}\mathcal{H}^T \mathcal{Q}^\prime \mathcal{G} K=Ip×p 0 0 ⋯ 0(HTQ′H+R′)−1HTQ′G，

计算可得 K = 2.6167 12.9286 K = \begin{bmatrix} 2.6167 \\ 12.9286 \end{bmatrix} K=2.616712.9286，MATLAB代码如下：

%% 选取K并检验系统是否稳定 
A = [1.1 2;0 0.95];
B = [0; 0.079];
K = [1.4 5.76];

eigSys = eig(A - B*K);
disp(abs(eigSys))
%% 求解P
K = [1.4 5.76];
Q = eye(2);
R = 0.1;
syms P [2 2] % P 为2*2的矩阵
equ = P - (A - B*K)' * P * (A - B*K) == Q + K'*R*K;
Psol = solve(equ, P);
Psol = [Psol.P1_1, Psol.P2_1; Psol.P2_1, Psol.P2_2];
Psol = double(Psol);
disp(Psol)
%% 计算G、H
N = 4;
[G, H] = getGH(N, A, B);
%% 计算Q、R、K
[Qp, Rp] = getQR(N, Q, Psol, R);
Kp = [eye(1), kron(ones(1, N-1), zeros(1))] * inv(H'*Qp*H + Rp)*H'*Qp*G;
% getGH等函数参见前面的博客

由 1.3 中可知观测增益 .

最终得到的系统的动态如下：

( L = 1.8342 0.3571 L = \begin{bmatrix} 1.8342 \\ 0.3571 \end{bmatrix} L=1.83420.3571)

( L = 1.0500 0.2263 L = \begin{bmatrix} 1.0500 \\ 0.2263 \end{bmatrix} L=1.05000.2263)

MATLAB演示代码：

A = [1.1 2;0 0.95];
B = [0; 0.079];
C = [1, 0];
K = [2.6167, 12.9286];
% L = [1.05; 0.2263];
L = [1.8342; 0.3571];

xCur = [1.2;-0.7]; % 设初始状态为[1;1]
xLog = xCur;
xHatCur = [0;0]; % 设初始状态为[0;0]
xHatLog = xHatCur;
uLog = [];

step = 0:50;
u = 0;
for i = step

    u = -K * xHatCur;

    yCur = C * xCur; % y_k
    xHatCur = A * xHatCur + B*u + L * (yCur - C * xHatCur); % xHat_k+1
    xCur = A*xCur + B*u; % x_k+1

    xHatLog = [xHatLog, xHatCur];
    xLog = [xLog, xCur];
    uLog = [uLog, u];
end

figure(1)
subplot(3,1,1)
hold on
plot(step, xLog(1,1:end-1))
plot(step, xHatLog(1,1:end-1))
title('x1')
grid on
subplot(3,1,2)
hold on
plot(step, xLog(2,1:end-1))
plot(step, xHatLog(2,1:end-1))
title('x2')
grid on
subplot(3,1,3)
plot(step, uLog)
title('u')
grid on