题目
证明
的MAP估计量为
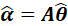
其中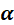
是一个的矢量,
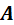是一个可逆的p*p的矩阵。也就是说，MAP估计量对可逆的线性变换是可以变换的。
解答
已知
的联合概率密度
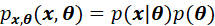
且：
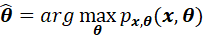
现在知道：
那么为了获得变换后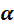
的MAP，首先需要根据
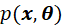求出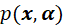
根据概率密度变换的基本知识：
（具体可以参考：随机过程------随机变量的函数变换(换元)_连续型分布函数的变换-CSDN博客）
又因为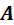
是可逆的，可以得到：
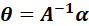
因此：
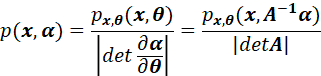
注意，上式本质上是雅可比行列式变换。由于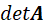
不包含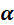
。因此，如果寻找不同
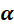下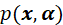
的最大值，等同于寻找不同
下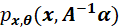
的最大值。而又根据
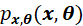的最大值出现在
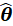处，那么根据线性关系，就可以得到此时的
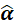就是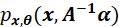
达到最大值对应的
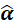，即：
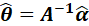
最后，再利用两个估计量的线性关系，得到：
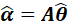
也就是MAP估计量（此例中的
）对可逆的线性变换（此例中的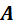
）,直接可以得到变换后新参数的MAP估计量（此例中的
）
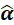注意MMSE估计量也有一样的线性性质，参见书（11.5）公式