数据结构——跳表Skip List

本文对跳表的定义、实现、应用等进行简单总结。

一、 介绍

1.定义

跳表（Skip List）：是一种概率性数据结构，由William Pugh在1990年提出，主要用于在有序的元素集合上进行快速的搜索、插入和删除操作。跳表的效率与平衡树相当，但实现起来更简单，它通过维护多层链表来提高查找效率。
2. 实现原理

在原有的有序链表上面增加了多级索引，通过索引进行二分查找从而实现高效率查找，其每种操作(搜索、插入、删除)的平均复杂性均为O(logn) 。
3.特点

特点	描述
结构	多层链表，每层是下层的子集。
查找效率	平均和最坏情况的时间复杂度均为 (O(\log n))，通过多层结构实现快速跳转。
插入效率	平均和最坏情况的时间复杂度也是 (O(\log n))，每个新元素通过随机机制决定其存在哪些层中。
删除效率	平均和最坏情况的时间复杂度为 (O(\log n))，通过定位到元素并在其存在的每层中删除。
空间复杂度	由于节点在多个层级中重复，空间复杂度较单一链表高。
实现简便	相较于平衡树和散列表，跳表的实现更直接，调整结构更简单。
用途	适用于需要大量动态插入和删除的有序数据集，如数据库和索引系统。

二、跳表的基本结构

1. 跳表是一组排序的链表，它们分层堆叠在一起，每个层级都包含了部分或全部元素，但每个上层都是下层的一个稀疏子集。

• 底层（Level 0）：包含所有元素的完整链表
• 上层：每一层都是下一层的稀疏子集，包含的元素逐层减少，每个元素向上晋级的概率通常是固定的（例如1/2）
• 节点：不仅包含数据，还包含指针：指向同层下一个节点、上层或下层的指针。
• 示例：
  

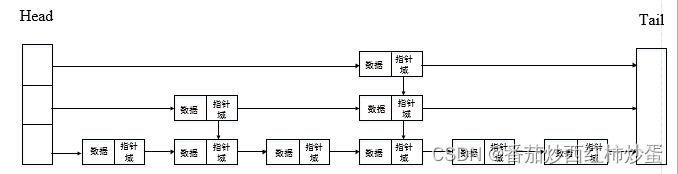
2. 跳表的基本操作
（1）查找操作

查找从最顶层开始，如果当前层的下一个节点值大于查找值，就下降到下一层继续查找，直到最底层。如果找到目标值，则查找成功；否则，查找失败。
（2）插入操作

插入元素时，先在底层插入该元素，然后通过抛硬币的方式（随机决定）决定是否将该元素提升到上层。这个过程可能会一直持续到顶层。
（3）删除操作

删除元素先找到该元素（如上所述的查找方式），然后从最底层向上逐层删除该元素。

三、跳表的应用

1. 数据库索引

• 快速查找：跳表提供了快速的查找性能，适合用作数据库中的索引结构，特别是在需要频繁插入和删除操作的数据库表中。
• 范围查询：跳表可以有效地支持范围查询，这使得它非常适合在需要进行范围搜索的数据库索引中使用。

2. 缓存系统

• 有序缓存：在缓存系统中，跳表可以用来保持缓存条目的有序性，便于实现如LRU（最近最少使用）等缓存淘汰算法。

3. 内存管理

• 动态内存分配：跳表可以用于动态内存分配器中，以追踪空闲内存块的大小和位置，快速分配和释放内存。

4. 并发编程

• 锁机制：跳表的结构使其更容易被分割成多个独立的部分，这样可以减少锁的竞争，适合并发环境。

5. 时间序列数据

• 股票和金融数据：跳表适合存储和查询时间序列数据，如股票价格和交易量，支持高效的插入和查询操作。

6. 网络路由

• 路由表：跳表可以用于网络路由表的实现，快速匹配IP地址和对应的路由。

7. 实时消息系统

• 消息排序和检索：在需要实时处理和检索大量有序消息的系统中，跳表提供了一个高效的解决方案。

8. 多级索引

• 文件系统索引：文件系统可以使用跳表来组织文件的元数据，特别是在需要频繁修改文件系统结构时。

四、Java实现跳表

1. 节点类定义

class SkipListNode<T> {
    T value;
    SkipListNode<T>[] forward; // 数组用来存储不同层的下一个节点

    public SkipListNode(int level, T value) {
        this.value = value;
        // 注意：数组索引从 0 开始，但是层级从 1 开始计数
        this.forward = new SkipListNode[level + 1];
    }
}

2. 跳表类定义

import java.util.Random;

class SkipList<T extends Comparable<? super T>> {
    private SkipListNode<T> head;
    private int maxLevel;
    private int level;
    private Random random;

    public SkipList() {
        // 最大层数设置为 16，实际应用中可以根据数据规模调整
        maxLevel = 16;
        level = 0;
        // 头节点的层级最大，所有层都有
        head = new SkipListNode<>(maxLevel, null);
        random = new Random();
    }

    // 生成随机层级
    private int randomLevel() {
        int lvl = 1;
        while (random.nextInt() % 2 == 0 && lvl < maxLevel) {
            lvl++;
        }
        return lvl;
    }

    // 查找方法
    public boolean search(T target) {
        SkipListNode<T> current = head;
        for (int i = level; i >= 0; i--) {
            while (current.forward[i] != null && current.forward[i].value.compareTo(target) < 0) {
                current = current.forward[i];
            }
        }
        current = current.forward[0];
        return current != null && current.value.compareTo(target) == 0;
    }

    // 插入方法
    public void insert(T value) {
        SkipListNode<T>[] update = new SkipListNode[maxLevel + 1];
        SkipListNode<T> current = head;
        for (int i = level; i >= 0; i--) {
            while (current.forward[i] != null && current.forward[i].value.compareTo(value) < 0) {
                current = current.forward[i];
            }
            update[i] = current;
        }
        current = current.forward[0];

        if (current == null || !current.value.equals(value)) {
            int lvl = randomLevel();
            if (lvl > level) {
                for (int i = level + 1; i <= lvl; i++) {
                    update[i] = head;
                }
                level = lvl;
            }
            SkipListNode<T> newNode = new SkipListNode<>(lvl, value);
            for (int i = 0; i <= lvl; i++) {
                newNode.forward[i] = update[i].forward[i];
                update[i].forward[i] = newNode;
            }
        }
    }

    // 删除方法
    public void delete(T value) {
        SkipListNode<T>[] update = new SkipListNode[maxLevel + 1];
        SkipListNode<T> current = head;
        for (int i = level; i >= 0; i--) {
            while (current.forward[i] != null && current.forward[i].value.compareTo(value) < 0) {
                current = current.forward[i];
            }
            update[i] = current;
        }
        current = current.forward[0];

        if (current != null && current.value.equals(value)) {
            for (int i = 0; i <= level; i++) {
                if (update[i].forward[i] != current) break;
                update[i].forward[i] = current.forward[i];
            }
            while (level > 0 && head.forward[level] == null) {
                level--;
            }
        }
    }
}

五、跳表与红黑树、B树、B+树

数据结构	平均查找时间复杂度	平均插入时间复杂度	平均删除时间复杂度	空间效率	实现复杂度	特点与应用场景
跳表	(O(\log n))	(O(\log n))	(O(\log n))	较低	较低	易于实现和理解，适用于需要快速插入和删除的场景，如缓存系统
红黑树	(O(\log n))	(O(\log n))	(O(\log n))	较高	高	保持平衡的二叉搜索树，适用于需要保持数据平衡的场景，如操作系统的各类调度
B树	(O(\log n))	(O(\log n))	(O(\log n))	高	高	广泛用于数据库和文件系统索引，优化磁盘读写效率和减少I/O操作
B+树	(O(\log n))	(O(\log n))	(O(\log n))	高	高	优化用于数据库和文件系统索引，叶节点互联提高区间查询效率