数据结构之栈和队列

栈

基础知识：

栈是一种逻辑结构，是特殊的线性表，特殊在只能在固定一端操作，具有"后进先出"的基本特征（泡腾片的取和放一样）

栈顶 : 可以进行插入删除的一端

栈底：栈顶的对端

入栈：将节点插入栈顶之上，也称为压栈，函数名通常为push()

出栈：将节点从栈顶剔除，也称为弹栈，函数名通常额外pop()

取栈顶: 取得栈顶元素，但不出栈，函数名通常为top()

存储方式

栈只是一种数据逻辑，可以采用顺序存储形成顺序栈或者采用链式存储形成链式栈。

顺序栈

cs 复制代码

// 顺序栈管理结构体
typedef struct 
{
    datatype *data; // 顺序栈入口
    int size;       // 顺序栈总容量
    int top;        // 顺序栈栈顶元素下标
}seqStack;


// 初始化空栈
seqStack *initStack(int size)
{
    seqStack *s = (seqStack *)malloc(sizeof(seqStack))
    if(s != NULL)
    {
        s->data = (datatype *)malloc(sizeof(datatype) * size));
        if(s->data == NULL)
        {
            free(s);
            return NULL;
        }
        s->size = size;
        s->top  = -1;
    }

    return s;
}

// 判断栈是否已满
bool isFull(seqStack *s)
{
    return s->top == s->size-1;
}

// 判断栈是否为空
bool isEmpty(seqStack *s)
{
    return s->top == -1;
}

// 入栈
bool push(seqStack *s, datatype data)
{
    if(isFull(s))
        return false;

    s->data[++s->top] = data;
    return true;
}

// 出栈
bool pop(seqStack *s, datatype *pm)
{
    if(top(s, pm) == false)
        return false;

    s->top--;
    return true;
}

// 取栈顶元素
bool top(seqStack *s, datatype *pm)
{
    if(isEmpty(s))
        return false;

    *pm = s->data[s->top];
    return true;
}

链式栈

cs 复制代码

// 链式栈节点
typedef struct node
{
    datatype data;
    struct node *next;
}node;

// 链式栈管理结构体
typedef struct linkStack
{
    node *top; // 链式栈栈顶指针
    int  size; // 链式栈当前元素个数
}linkStack;

// 初始化空栈
linkStack * initStack(void)
{
	linkStack * s = (linkStack *)malloc(sizeof(linkStack));
    if(s != NULL)
    {
        s->top  = NULL;
        s->size = 0;
    }
	return s;
}

// 判断栈是否为空
bool isEmpty(linkStack *s)
{
	return (top->size == 0);
}

// 入栈
bool push(linkStack *s, datatype data)
{
    // 创建链表节点
    node *new = (node *)malloc(sizeof(node));
	if(new == NULL)
		return false;

	new->data = data;

    // 将节点置入栈顶
	new->next = s->top;
	s->top = new;

    // 更新栈元素个数
    s->size++;
	return true;
}

// 出栈
bool pop(linkStack *s, datatype *pm)
{
	if(isEmpty(s))
		return false;

	linkStack *tmp = s->top;

    // 将原栈顶元素剔除出栈
	s->top    = tmp->next;
    tmp->next = NULL;

    // 返回栈顶元素，并释放节点
    *pm = tmp->data;
	free(tmp);

	return true;
}

// 取栈顶元素
bool top(linkStack *s, datatype *pm)
{
	if(isEmpty(s))
		return false;

    // 返回栈顶元素，并释放节点
    *pm = s->top->data;
	return true;
}

队列

只能在固定的两端操作线性表，呈现一种"先进先出"的逻辑。

基础知识：

队头：可以删除节点的一端

队尾：可以插入节点的一端

入队：将节点插入到队尾之后，函数名通常为enQueue()

出队：将队头节点从队列中剔除，函数名通常为outQueue()

取队头：取得队头元素，但不出队，函数名通常为front()

存储方式

与其他的逻辑结构类似，队列可以采用顺序存储形成循环队列，也可以采用链式存储形成链式队列。

循环队列

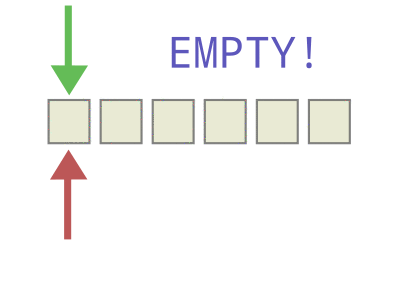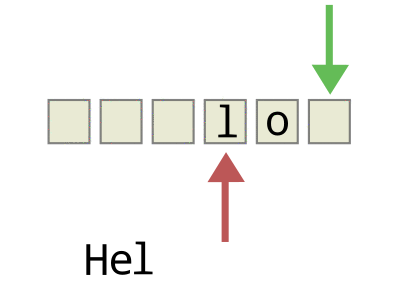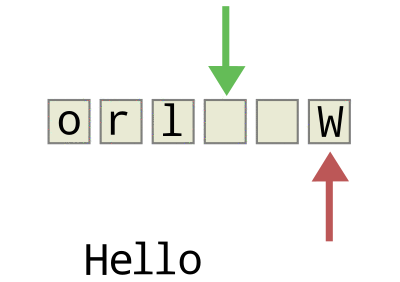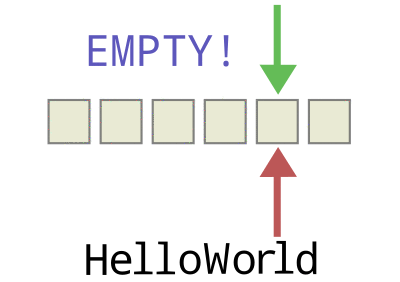
如图，头指针+1= 尾指针则队列为满，尾指针=头指针则队列为空。

cs 复制代码

struct seqQueue
{
    datatype *data; // 循环队列入口
    int capacity;   // 循环队列总容量
    int front;      // 循环队列队头元素下标
    int rear;       // 循环队列队头元素下标
};
// 初始化空队列
seqQueue * initQueue(int cap)
{
	*pq = (sequeue *)malloc(sizeof(sequeue));
	(*pq)->front = (*pq)->rear = MAXSIZE - 1;
}

// 判断队列是否为空
bool isEmpty(seqQueue *q)
{
	return q->front == q->rear;
}

// 判断队列是否已满
bool isFull(seqQueue *q)
{
	return (q->rear+1)%q->capacity == q->front;
}

// 出队
bool outQueue(seqQueue *q, datatype *pm)
{
	if(isEmpty(q))
		return false;

	*pm = q->data[q->front];
	q->front = (q->front + 1) % q->capacity;

	return true;
}

// 入队
bool enQueue(seqQueue *q, datatype data)
{
	if(isFull(q))	
		return false;

	q->data[q->rear] = data;
	q->rear = (q->rear + 1) % q->capacity;

	return true;
}

链式队列

链式队列的组织形式与链表无异，只不过插入删除被约束在固定的两端。

cs 复制代码

// 链式队列节点
typedef struct node
{
    datatype data;
    struct node *next;
}node;

// 链式队列管理结构体
typedef struct
{
    node *front; // 队头指针
    node *rear;  // 队尾指针

    int  size;   // 队列当前元素个数
}linkQueue;
// 初始化空队列
linkQueue *initQueue()
{
    linkQueue *q = (linkQueue *)malloc(sizeof(linkQueue))
    if(q != NULL)
    {
        q->front = NULL;
        q->rear  = NULL;
        
        q->size  = 0;
    }

    return q;
}

// 判断队列是否为空
bool isEmpty(linkQueue *q)
{
    return q->size == 0;
}

// 入队
bool enQueue(linkQueue *q, datatype data)
{
    // 创建新节点
    node *new = malloc(sizeof(node));
    if(new == NULL)
        return false;

    new->data = data;
    new->next = NULL;

    // 入队分两种情况：
    // 1. 当前队列为空，则新节点是队列的唯一节点
    if(isEmpty(q))
        q->front = q->rear = new;

    // 2. 否则队列不为空，将新节点拼接到队尾之后
    else
    {
        q->rear->next = new;
        q->rear = new;
    }

    q->size++;
    return true;
}

// 出队
bool outQueue(linkQueue *q, datatype *pm)
{
    if(isEmpty(q))
        return false;

    // 返回用户数据
    *pm = q->front->data;

    // 更新队头队尾指针，分两种情况：
    // 1. 当前队列只有一个元素，出队后队列为空，此时队头队尾指针都必须更新
    if(q->size == 1)
    {
        free(q->front);
        q->front = NULL;
        q->rear  = NULL;
    }

    // 2. 否则，只需更新队头指针即可
    else
    {
        node *tmp = q->front;
        q->front = q->front->next;

        tmp->next = NULL;
        free(tmp);
    }

    q->size--;
    return true;
}

// 取队头元素
bool front(linkQueue *q, datatype *pm)
{
    if(isEmpty(q))
        return false;

    *pm = q->front->data;
    return true;
}