本篇来自对线性代数第一篇的行列式的一个总结。
主要是行列式中有些关键点和注意事项,便于之后的考研复习使用。
首先,对于普通的二阶和三阶行列式,我们可以直接对其进行拆开,展开。
而对于n阶行列式
其行列式的值等于它的任意一行或者一列与其对应的代数余子项的乘积之和
其中我们称



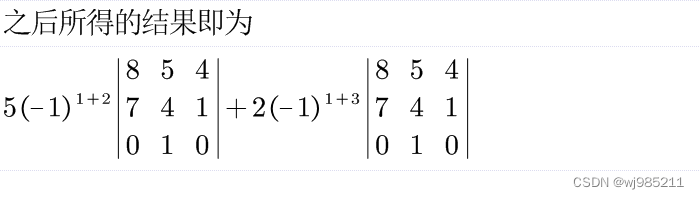
之后便是算数的过程.........
我知道行列式的展开讲述起来是一个抽象的过程,要想真正了解其还是得看书做题。
关于范德蒙行列式
这其实算是和点火公式一类,相当于公式一般记住就行
其特点是,第一行全是1,第二行为正常的元素,而第三行则为第二行相对应的元素的两次,第四行则为相对于第二行元素的三次,如此我们称该行列式为范德蒙行列式,
那么最终的结果即为,第二项减去第一项,乘,第三项减去第一项.....到第n项减去第一项(注意,此项目相减只发生在第二行,即为正常的元素)如此,所有的元素都减过了第一项,该所有的元素减去第二项(除去第一项),同理,到了第三项,所有元素减去第三项(除去第二项和第一项)。注意该最终的结果是所有相减的差相乘。
小总结
关于行列式,是一个难以表达,又是十分抽象的过程,我看了自己的过程,感觉就是完全不能拿到台面上的作品,其中的过程完全不能给那些初学者所表述清楚。可能这也是和我是初学者有关,我也是刚看完网课,对于行列式有了一个初步的概念,关于之后如何再来完备自己的行列式的框架,那就之后再看吧,对于行列式,还是要在题目之中找到做题的理解和概念。