offer7.重建二叉树

根据二叉树的前序遍历和中序遍历重建二叉树

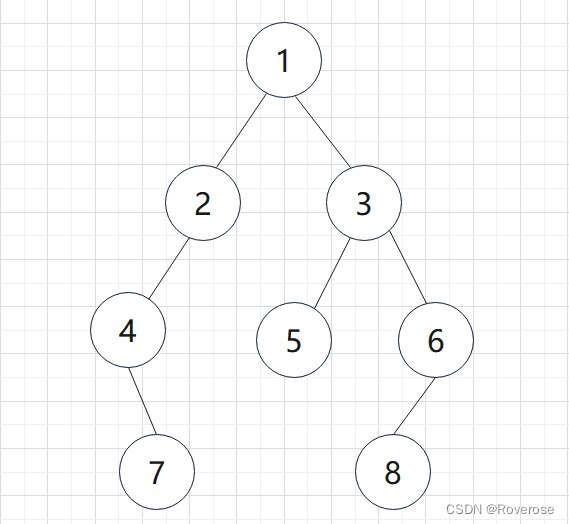
问题描述：输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如，输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建如下图所示的二叉树并输出它的头节点。

二叉树的定义如下：

cpp 复制代码

struct TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
};

解题思路：前序遍历中的第一个数字即为根节点的值，二叉树节点的值各不相同，那么可以扫描中序遍历数组中找到根节点值所在下标位置。又根据中序遍历的特点，在根节点左边的所有数值为根节点的左子树，在根节点右边的所有数值为根节点的右子树。或以得到根节点左右子树中序遍历和先序遍历两个子数组，然后可以递归重建它的左右子树，最后完成整棵二叉树的重建。

cpp 复制代码

TreeNode* Construct(int* preorder,int* inorder,int length){           //通进先序遍历和中序遍历确定一棵二叉树
  if(preorder == nullptr || inorder == nullptr || length <= 0){
    return nullptr;
  }
  return ConstructCore(preorder,preorder + length - 1,inorder,inorder + length - 1);
}

TreeNode* ConstructCore(int* startPreorder,int* endPreorder,int* startInorder,int* endInorder){
  //前序遍历第一个数字是根节点的值
  int rootValue = startPreorder[0];
  TreeNode* root = new TreeNode();    //新建一个二叉树节点
  root->val = rootValue;
  root->left = root->right = nullptr;
  if(startPreorder == endPreorder){
    if(startInorder == endInorder && *startPreorder == *startInorder){
      return root;                              //如果当前节点是最后一个节点，没有后继节点则返回
    }
    else{
      throw exception();
    }
  }
  //在中序遍历序列中找到根节点的值
  int* rootInorder = startInorder;
  while(rootInorder <= endInorder && *rootInorder != rootValue){
    rootInorder++;
  }
  if(rootInorder == endInorder && *rootInorder != rootValue){
    throw exception();                        //如果根节点不存在，则抛出异常
  }

  int leftLength = rootInorder - startInorder;      //左子树 中序和前序数组的长度
  int *leftPreorderEnd = startPreorder + leftLength;    //左子树------数组的终点
  if(leftLength > 0){
    //构建左子树
    root->left = ConstructCore(startPreorder + 1,leftPreorderEnd,startInorder,rootInorder - 1);
  }
  if(leftLength < endPreorder - startPreorder){
    //构建右子树
    root->right = ConstructCore(leftPreorderEnd + 1,endPreorder,rootInorder + 1,endInorder);
  }
  return root;
}

可以通过main函数调用进行验证:

cpp 复制代码

#include <iostream>
using namespace std;

int main(){
  
  //由前序遍历和中序遍历构造出完整的二叉树
  int preorder[10] = {1,2,4,7,3,5,6,8,9,10};
  int inorder[10] = {4,7,2,1,5,3,8,6,9,10};

  TreeNode* root = Construct(preorder,inorder,10);
  dfs(root);        //通过dfs打印二叉树的节点
  cout<<endl;

    return 0;
}

 void dfs(TreeNode* root){
    if(root == nullptr)
        return;
    dfs(root->left);
    cout<<root->val<<" ";
    dfs(root->right);
}