算法竞赛---宽度优先遍历求解最短路径问题（方向数组里面是4个元素）

下面的这两个题目依然是属于这个宽度优先遍历的题目解析：

1.小明的看电影问题

和上一篇文章里面的内容有所区别，在这个小明看电影的问题里面，这个方向只有上下左右四个方向，之前无论是这个马儿的问题，还是骑士风度的牛的这个问题，都是存在着八种情况的；

但是在下面的这个问题里面，其实是只有四个情况，而且这个存在无法到达目的地的这个情况，这个也是需要我们去进行处理的；

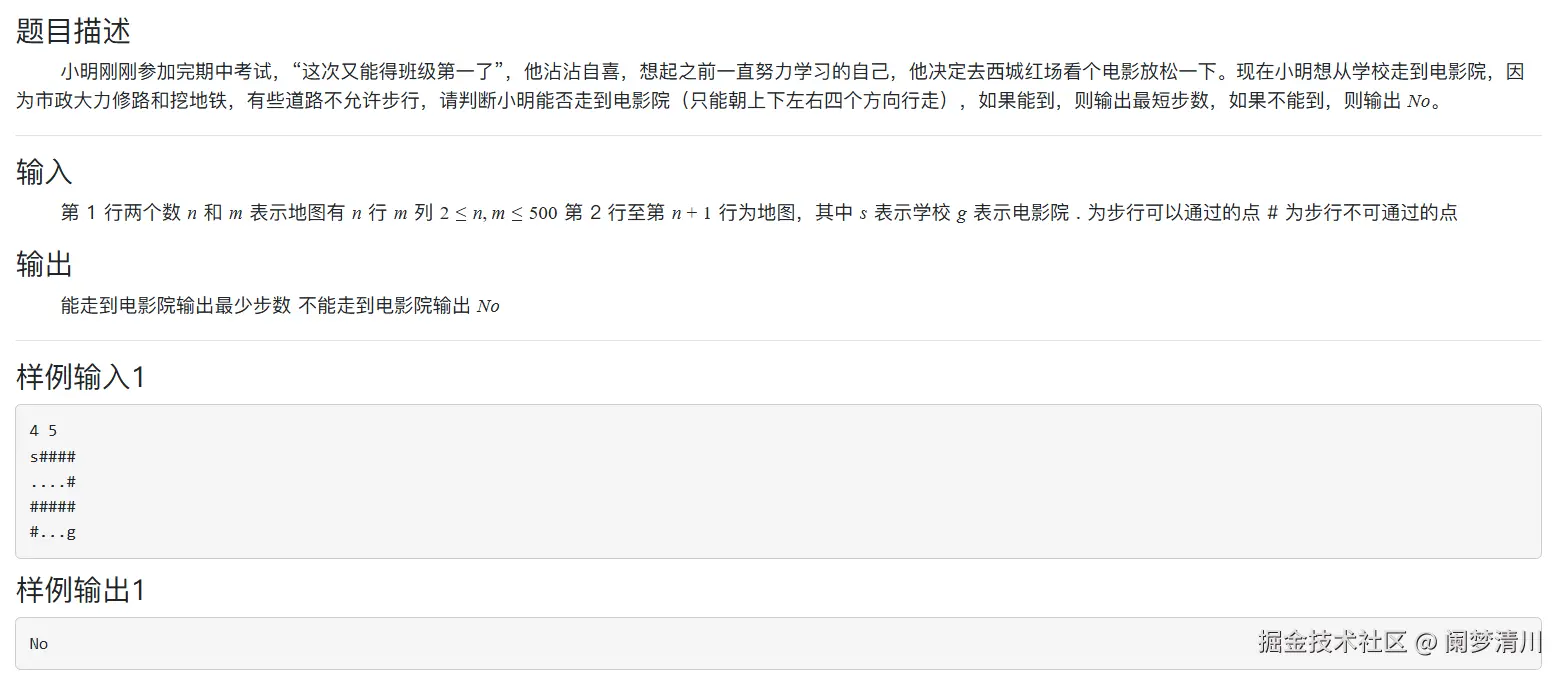
下面的这个就是我们的代码：

1）首先针对于这个问题里面涉及到的这个方向数组，因为就是上下左右几种情况，因此这个里面，方向数组里面只有四个元素；

2）第一个for循环主要进行的就是这个数据的输入的过程，并且识别到这个s的时候存储为我们的这个过程的起始位置的具体的坐标；

3）经过这个宽度优先遍历的过程之后，我们再次使用两个循环，找到这个里面的元素是g的位置，输出这个具体的具体，也就是这个dist数组里面的内容，并且需要保证这个不是-1，因为这个-1表示的是我们的初始情况，没有遍历到的位置，也就是初始化的这个数字，如果是-1的话，表示这个是没有被处理到的；

4）因为这个如果找不到，需要输出no这个内容，因此我在这个里面设计了一个标志位，使用布尔值进行表示，如果这个过程中找到了这个g，这个时候我们就修改这个标志位的内容，针对于这个没有找到的处理，我们需要使用这个标志位进行判断一下的；

ini 复制代码

//#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n, m;
int x, y;
typedef pair<int, int> PII;
const int N = 505;
char a[N][N];
int dist[N][N];


int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };

void bfs()
{
    memset(dist, -1, sizeof(dist));
    queue<PII> q;
    q.push({ x,y });
    dist[x][y] = 0;

    while (q.size())
    {
        auto t = q.front(); q.pop();
        int i = t.first, j = t.second;
        for (int k = 0; k < 4; k++)
        {
            int x = i + dx[k], y = j + dy[k];
            if (x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] != '#' && dist[x][y] == -1)
            {
                dist[x][y] = dist[i][j] + 1;
                q.push({ x, y });
            }
        }
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
            if (a[i][j] == 's')
            {
                x = i, y = j;
            }
        }
    }

    bfs();
    
    bool found=false;

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j] == 'g' && dist[i][j] != -1)
            {
                cout << dist[i][j] << endl;
                found=true;
            }
        }
    }
    if(found==false)
        {
        cout<<"No"<<endl;
    }
    //cout << "No" << endl;
    return 0;
}

2.小明吃饭问题

下面的这个就是小明的吃饭问题，场景式大同小异，这个代码也就是稍微修改一下就可以通过测试的：

下面的这个是题目：下面的这个题目里面的要点我都是用这个红框框为大家框选出来了；

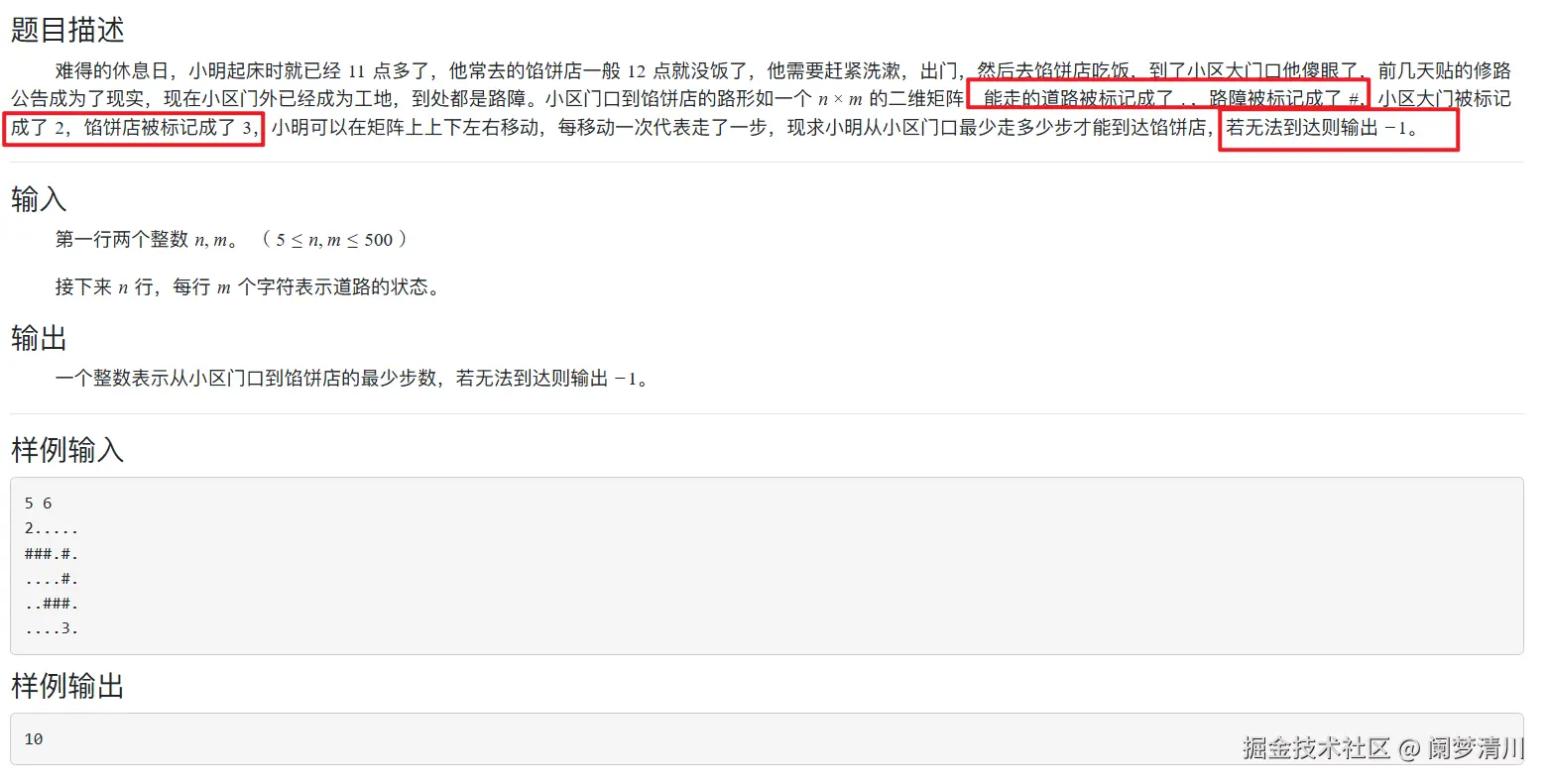
下面的这个是代码：

1）首先这个规定的还是上下左右四个方向，并且这个路障设么标记之类的进行了变化，其他的这个代码都是不需要进行任何的修改的；

2）然后就是这个里面如果没有找到，需要输出的事-1，这个也是需要进行修改的，

3）除了上面介绍的这个路障，终点的标志发生了变化，还有就是没有找到的时候输出的内容发生了变化，其他的这个代码都不需要发生任何的变化，因此如果你知道这个具体的逻辑，你就很容易面对一个新的题目，直到在哪里进行修改，能够很快的进行处理，证明你对于bfs求解最短路径问题就掌握的还算是不错了；

ini 复制代码

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n, m;
int x, y;
typedef pair<int, int> PII;
const int N = 505;
char a[N][N];
int dist[N][N];


int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };

void bfs()
{
    memset(dist, -1, sizeof(dist));
    queue<PII> q;
    q.push({ x,y });
    dist[x][y] = 0;

    while (q.size())
    {
        auto t = q.front(); q.pop();
        int i = t.first, j = t.second;
        for (int k = 0; k < 4; k++)
        {
            int x = i + dx[k], y = j + dy[k];
            if (x >= 1 && x <= n && y >= 1 && y <= m && a[x][y] != '#' && dist[x][y] == -1)
            {
                dist[x][y] = dist[i][j] + 1;
                q.push({ x, y });
            }
        }
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> a[i][j];
            if (a[i][j] == '2')
            {
                x = i, y = j;
            }
        }
    }

    bfs();
    
    bool found=false;

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            if (a[i][j] == '3' && dist[i][j] != -1)
            {
                cout << dist[i][j] << endl;
                found=true;
                
            }
        }
    }
    if(found==false)
        {
        cout<<"-1"<<endl;
    }
    //cout << "No" << endl;
    return 0;
}