https://blog.csdn.net/weixin_43334693/article/details/130189238
https://blog.csdn.net/weixin_47936614/article/details/130466448
注意力机制:在处理信息的时候,会将注意力放在需要关注的信息上,对于其他无关的外部信息进行过滤,这种处理方式被称为注意力机制。
注意力机制可以使模型在处理序列数据时更加准确和有效。在传统的神经网络中,每个神经元的输出只依赖于前一层的所有神经元的输出,而在注意力机制中,每个神经元的输出不仅仅取决于前一层的所有神经元的输出,还可以根据输入数据的不同部分进行加权,即对不同部分赋予不同的权重。这样可以使模型更加关注输入序列中的关键信息,从而提高模型的精度和效率。
注意力机制原理
1.计算注意力权重:注意力机制的第一步是计算每个输入位置的注意力权重。这个权重可以根据输入数据的不同部分进行加权,即对不同部分赋予不同的权重。权重的计算通常是基于输入数据和模型参数的函数,可以使用不同的方式进行计算,比如点积注意力、加性注意力、自注意力等。
2.加权求和输入表示:计算出注意力权重之后,下一步就是将每个输入位置的表示和对应的注意力权重相乘,并对所有加权结果进行求和。这样可以得到一个加权的输入表示,它可以更好地反映输入数据中重要的部分。
3.计算输出:注意力机制的最后一步是根据加权的输入表示和其他模型参数计算输出结果。这个输出结果可以作为下一层的输入,也可以作为最终的输出。
需要注意的是,注意力机制并不是一种特定的神经网络结构,而是一种通用的机制,可以应用于不同的神经网络结构中。比如,可以在卷积神经网络中使用注意力机制来关注输入图像中的重要区域,也可以在循环神经网络中使用注意力机制来关注输入序列中的重要部分。
查询(Query): 指的是查询的范围,自主提示,即主观意识的特征向量
键(Key): 指的是被比对的项,非自主提示,即物体的突出特征信息向量
值(Value) : 则是代表物体本身的特征向量,通常和Key成对出现
注意力机制是通过Query与Key的注意力汇聚(给定一个 Query,计算Query与 Key的相关性,然后根据Query与Key的相关性去找到最合适的 Value)实现对Value的注意力权重分配,生成最终的输出结果。
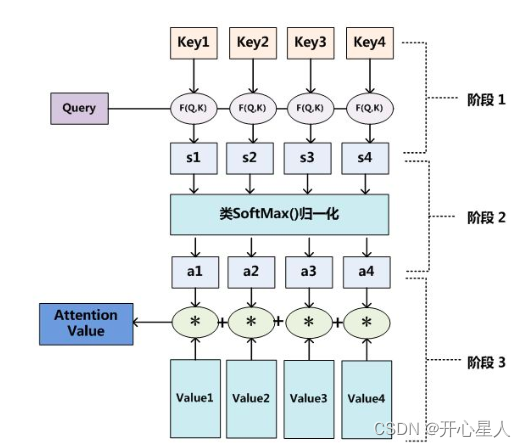
注意力机制计算过程:
阶段1、根据Query和Key计算两者之间的相关性或相似性(常见方法点积、余弦相似度,MLP网络),得到注意力得分

阶段2、对注意力得分进行缩放scale(除以维度的根号),再softmax函数,一方面可以进行归一化,将原始计算分值整理成所有元素权重之和为1的概率分布;另一方面也可以通过softmax的内在机制更加突出重要元素的权重。一般采用如下公式计算
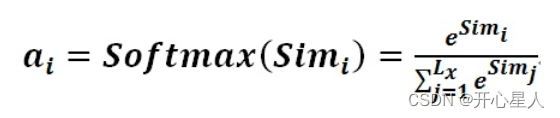
阶段3、根据权重系数对Value值进行加权求和,得到Attention Value(此时的V是具有一些注意力信息的,更重要的信息更关注,不重要的信息被忽视了)
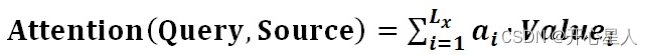
自注意力机制
神经网络接收的输入是很多大小不一的向量,并且不同向量向量之间有一定的关系,但是实际训练的时候无法充分发挥这些输入之间的关系而导致模型训练结果效果极差。比如机器翻译(序列到序列的问题,机器自己决定多少个标签),词性标注(Pos tagging一个向量对应一个标签),语义分析(多个向量对应一个标签)等文字处理问题。
自注意力机制实际上是想让机器注意到整个输入中不同部分之间的相关性
自注意力机制是注意力机制的变体,其减少了对外部信息的依赖,更擅长捕捉数据或特征的内部相关性。自注意力机制的关键点在于,Q、K、V是同一个东西,或者三者来源于同一个X,三者同源。通过X找到X里面的关键点,从而更关注X的关键信息,忽略X的不重要信息。不是输入语句和输出语句之间的注意力机制,而是输入语句内部元素之间或者输出语句内部元素之间发生的注意力机制。
自注意力机制原理
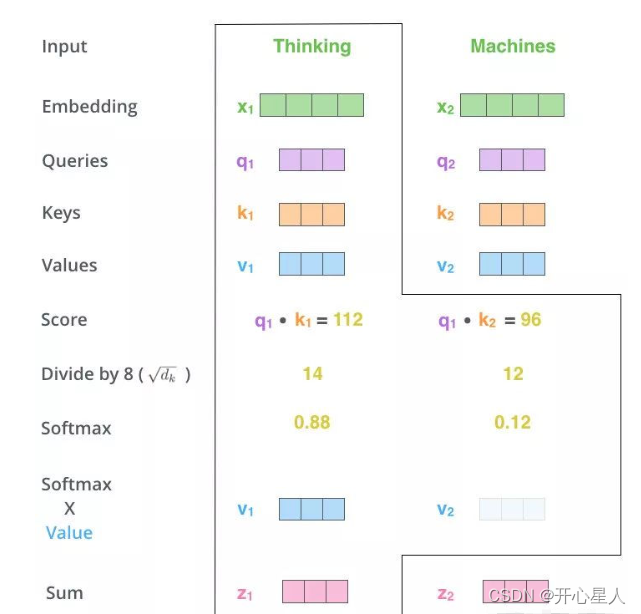
1、得到Q,K,V的值
对于每一个向量x,分别乘上三个系数 Wq,Wk,Wv,得到的Q,K和V分别表示query,key和value (这三个W就是我们需要学习的参数)
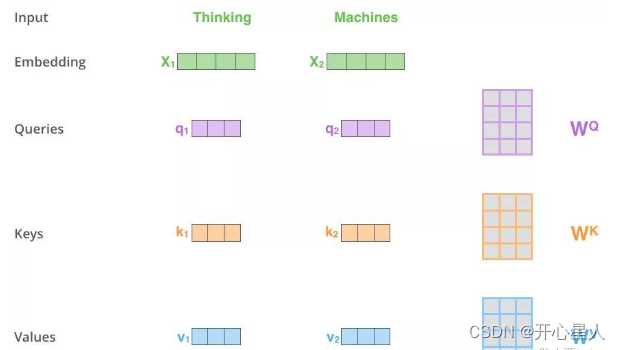
2、计算注意力权重
利用得到的Q和K计算每两个输入向量之间的相关性,一般采用点积计算
3、Scale+Softmax
将刚得到的相似度除以 d k \sqrt{d~k~} d k (dk 表示键向量的维度),再进行Softmax。经过Softmax的归一化后,每个值是一个大于0且小于1的权重系数,且总和为1,这个结果可以被理解成一个权重矩阵。
4、使用刚得到的权重矩阵,与V相乘,计算加权求和。
自注意力机制问题:
1、自注意力机制的原理是筛选重要信息,过滤不重要信息。这就导致自注意力机制无法完全利用图像本身具有的尺度,平移不变性,以及图像的特征局部性。这就导致自注意力机制只有在大数据的基础上才能有效地建立准确的全局关系
2、自注意力机制虽然考虑了所有的输入向量,但没有考虑到向量的位置信息。在实际的文字处理问题中,可能在不同位置词语具有不同的性质(可通过位置编码解决:对每一个输入向量加上一个位置向量e,位置向量的生成方式有多种,通过e来表示位置信息带入self-attention层进行计算)
多头注意力机制:Multi-Head Self-Attention
多头注意力机制在自注意力的基础上,通过增加多个注意力头来并行地对输入信息进行不同维度的注意力分配,从而捕获更丰富的特征和上下文信息。
第1步:定义多组W,生成多组Q、K、V
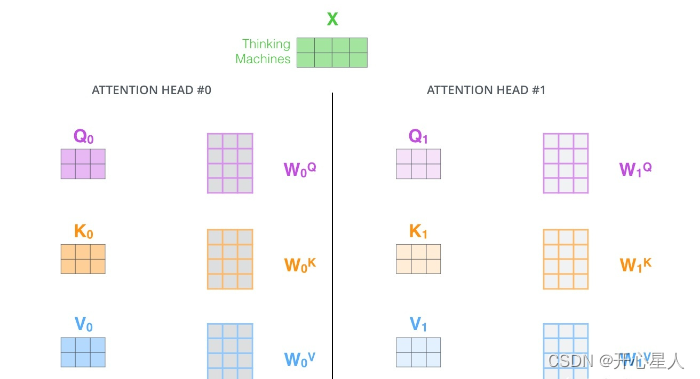
线性变换:首先,对输入序列中的每个位置的向量分别进行三次线性变换(即加权和偏置),生成查询矩阵Q, 键矩阵K, 和值矩阵V。在多头注意力中,这一步骤实际上会进行h次(其中h为头数),每个头拥有独立的权重矩阵,从而将输入向量分割到h个不同的子空间。
第2步:
并行注意力计算:对每个子空间,应用自注意力机制计算注意力权重,并据此加权求和值矩阵V,得到每个头的输出。公式上表现为:
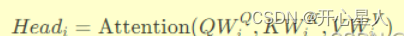
第3步:
合并与最终变换:将所有头的输出拼接起来,再经过一个最终的线性变换和层归一化,得到多头注意力的输出。这一步骤整合了不同子空间学到的信息,增强模型的表达能力。
python
import torch
from torch.nn import Module, Linear, Dropout, LayerNorm
class MultiHeadAttention(Module):
def __init__(self, d_model, num_heads, dropout=0.1):
super(MultiHeadAttention, self).__init__()
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
self.d_head = d_model // num_heads
self.num_heads = num_heads
self.linear_q = Linear(d_model, d_model)
self.linear_k = Linear(d_model, d_model)
self.linear_v = Linear(d_model, d_model)
self.linear_out = Linear(d_model, d_model)
self.dropout = Dropout(dropout)
self.layer_norm = LayerNorm(d_model)
def forward(self, q, k, v, mask=None):
batch_size = q.size(0)
# 线性变换
q = self.linear_q(q).view(batch_size, -1, self.num_heads, self.d_head)
k = self.linear_k(k).view(batch_size, -1, self.num_heads, self.d_head)
v = self.linear_v(v).view(batch_size, -1, self.num_heads, self.d_head)
# 转置以便于计算注意力
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
# 计算注意力权重
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(self.d_head)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
attn_weights = torch.softmax(scores, dim=-1)
attn_weights = self.dropout(attn_weights)
# 加权求和得到输出
outputs = torch.matmul(attn_weights, v)
# 转换回原始形状并进行最终线性变换
outputs = outputs.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)
outputs = self.linear_out(outputs)
outputs = self.layer_norm(outputs + q)
return outputs