DAY19-力扣刷题

1.平衡二叉树

给定一个二叉树，判断它是否是平衡二叉树

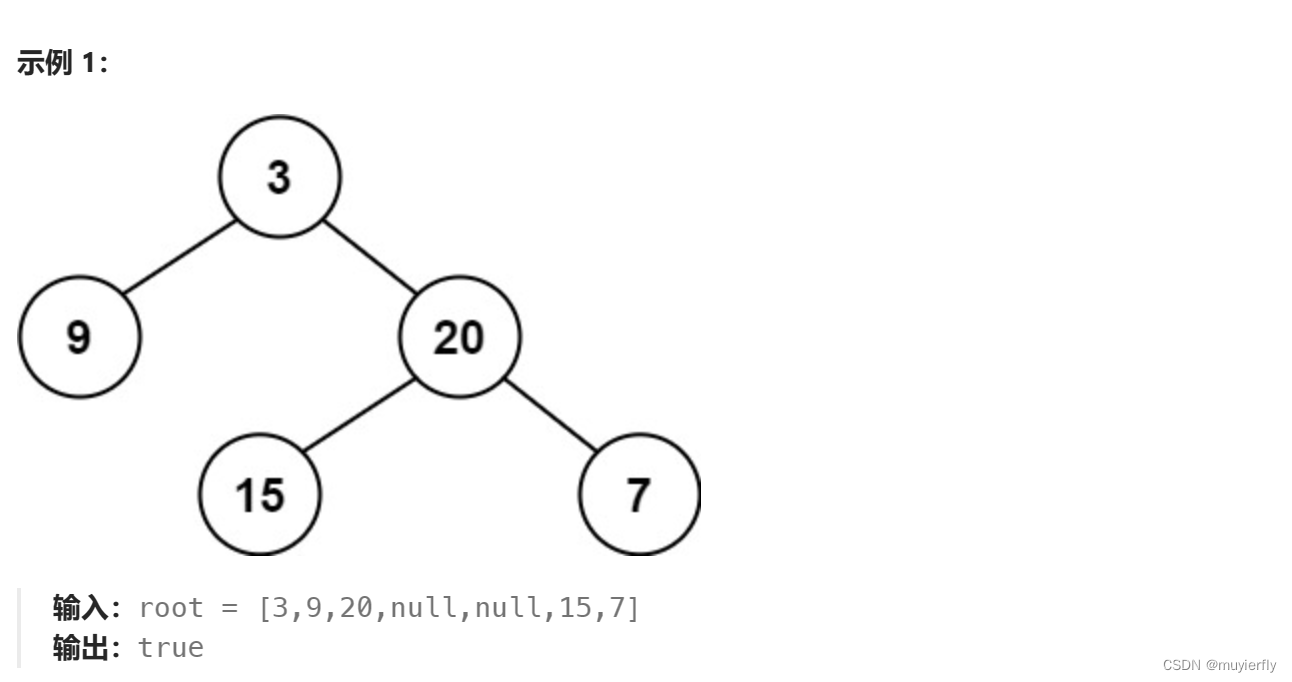
java 复制代码

class Solution {
    public int getHeight(TreeNode root) {
            if(root == null)
                return 0;
            int leftHeight = getHeight(root.left);
            int rightHeight = getHeight(root.right);
            if(leftHeight>=0&&rightHeight>=0&&Math.abs(leftHeight-rightHeight)<=1){
                return Math.max(leftHeight,rightHeight)+1;
            }else{
                return -1;
            }
            
        }
    public boolean isBalanced(TreeNode root) {
        if(root==null){
            return true;
        }
        return getHeight(root)>=0;
    }
}

2.二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

111. 二叉树的最小深度 - 力扣（LeetCode）

java 复制代码

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        if (root.left == null && root.right == null) {
            return 1;
        }

        int min_depth = Integer.MAX_VALUE;
        if (root.left != null) {
            min_depth = Math.min(minDepth(root.left), min_depth);
        }
        if (root.right != null) {
            min_depth = Math.min(minDepth(root.right), min_depth);
        }

        return min_depth + 1;
    }
}

3.路经总和

112. 路径总和 - 力扣（LeetCode）

方法一：广度优先搜索

java 复制代码

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        Queue<TreeNode> queNode = new LinkedList<TreeNode>();
        Queue<Integer> queVal = new LinkedList<Integer>();
        queNode.offer(root);
        queVal.offer(root.val);
        while (!queNode.isEmpty()) {
            TreeNode now = queNode.poll();
            int temp = queVal.poll();
            if (now.left == null && now.right == null) {
                if (temp == sum) {
                    return true;
                }
                continue;
            }
            if (now.left != null) {
                queNode.offer(now.left);
                queVal.offer(now.left.val + temp);
            }
            if (now.right != null) {
                queNode.offer(now.right);
                queVal.offer(now.right.val + temp);
            }
        }
        return false;
    }
}

方法二:递归

java 复制代码

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}

4.路经总和2

113. 路径总和 II - 力扣（LeetCode）

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

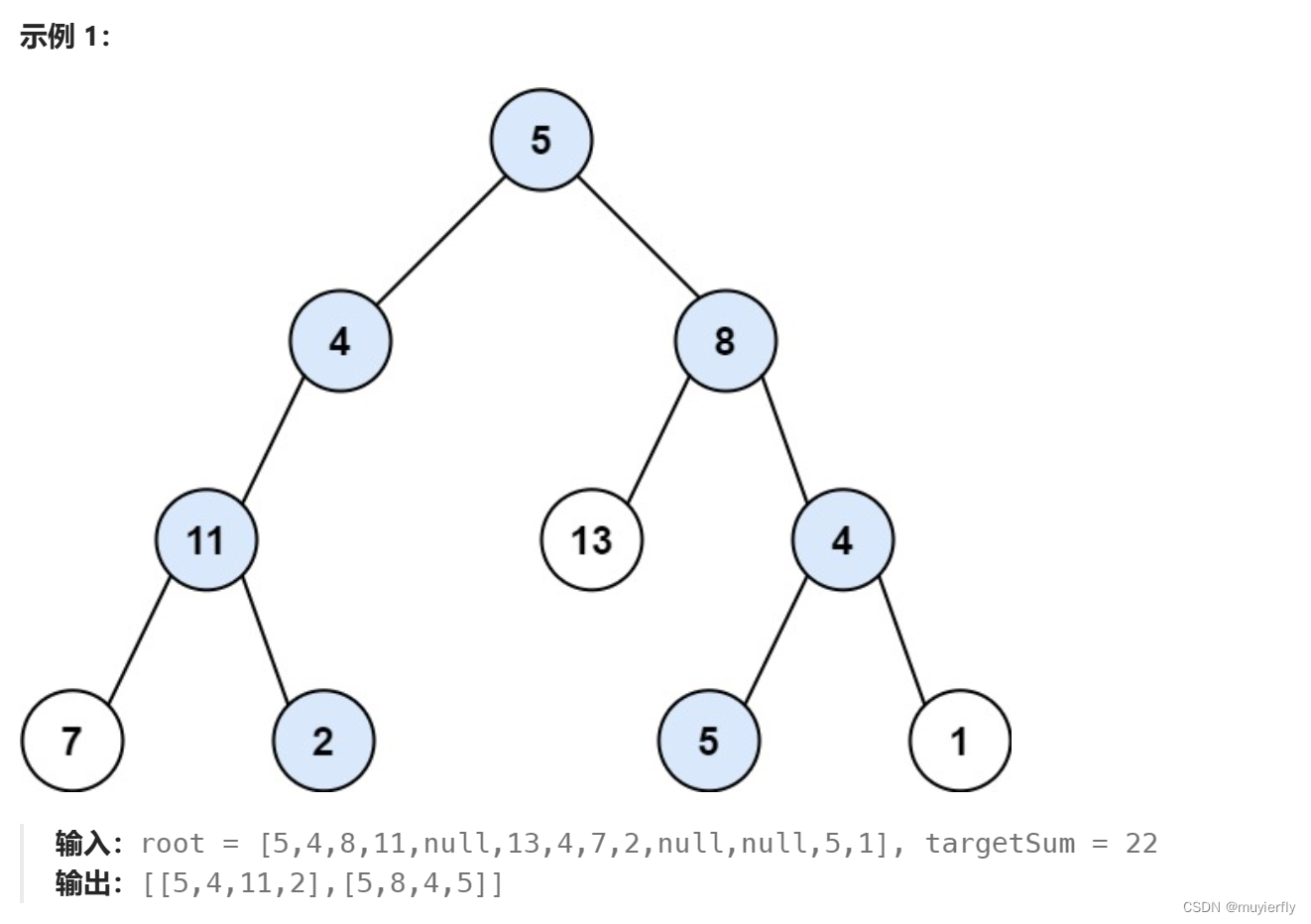
方法一：深度优先搜索

java 复制代码

class Solution {
    List<List<Integer>> ret = new LinkedList<List<Integer>>();
    Deque<Integer> path = new LinkedList<Integer>();

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        dfs(root, targetSum);
        return ret;
    }

    public void dfs(TreeNode root, int targetSum) {
        if (root == null) {
            return;
        }
        path.offerLast(root.val);
        targetSum -= root.val;
        if (root.left == null && root.right == null && targetSum == 0) {
            ret.add(new LinkedList<Integer>(path));
        }
        dfs(root.left, targetSum);
        dfs(root.right, targetSum);
        path.pollLast();
    }
}

方法二：广度优先搜索

java 复制代码

class Solution {
    List<List<Integer>> ret = new LinkedList<List<Integer>>();
    Map<TreeNode, TreeNode> map = new HashMap<TreeNode, TreeNode>();

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return ret;
        }

        Queue<TreeNode> queueNode = new LinkedList<TreeNode>();
        Queue<Integer> queueSum = new LinkedList<Integer>();
        queueNode.offer(root);
        queueSum.offer(0);

        while (!queueNode.isEmpty()) {
            TreeNode node = queueNode.poll();
            int rec = queueSum.poll() + node.val;

            if (node.left == null && node.right == null) {
                if (rec == targetSum) {
                    getPath(node);
                }
            } else {
                if (node.left != null) {
                    map.put(node.left, node);
                    queueNode.offer(node.left);
                    queueSum.offer(rec);
                }
                if (node.right != null) {
                    map.put(node.right, node);
                    queueNode.offer(node.right);
                    queueSum.offer(rec);
                }
            }
        }

        return ret;
    }

    public void getPath(TreeNode node) {
        List<Integer> temp = new LinkedList<Integer>();
        while (node != null) {
            temp.add(node.val);
            node = map.get(node);
        }
        Collections.reverse(temp);
        ret.add(new LinkedList<Integer>(temp));
    }
}

5.二叉树展开为链表

114. 二叉树展开为链表 - 力扣（LeetCode）

方法一:前序遍历

java 复制代码

class Solution {
    public void flatten(TreeNode root) {
        List<TreeNode> list = new ArrayList<TreeNode>();
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode node = root;
        while (node != null || !stack.isEmpty()) {
            while (node != null) {
                list.add(node);
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            node = node.right;
        }
        int size = list.size();
        for (int i = 1; i < size; i++) {
            TreeNode prev = list.get(i - 1), curr = list.get(i);
            prev.left = null;
            prev.right = curr;
        }
    }
}

方法二:寻找前驱节点

java 复制代码

class Solution {
    public void flatten(TreeNode root) {
        TreeNode curr = root;
        while (curr != null) {
            if (curr.left != null) {
                TreeNode next = curr.left;
                TreeNode predecessor = next;
                while (predecessor.right != null) {
                    predecessor = predecessor.right;
                }
                predecessor.right = curr.right;
                curr.left = null;
                curr.right = next;
            }
            curr = curr.right;
        }
    }
}