Financial Markets
本文是学习 https://www.coursera.org/learn/financial-markets-global这门课的学习笔记
这门课的老师是耶鲁大学的Robert Shiller https://en.wikipedia.org/wiki/Robert_J._Shiller

Robert James Shiller (born March 29, 1946)[4] is an American economist, academic, and author. As of 2022,[5] he served as a Sterling Professor of Economics at Yale University and is a fellow at the Yale School of Management's International Center for Finance.[6] Shiller has been a research associate of the National Bureau of Economic Research (NBER) since 1980, was vice president of the American Economic Association in 2005, its president-elect for 2016, and president of the Eastern Economic Association for 2006--2007.[7] He is also the co‑founder and chief economist of the investment management firm MacroMarkets LLC.
Week 3
Stocks, bonds, dividends, shares, market caps; what are these? Who needs them? Why? Module 3 explores these concepts, along with corporation basics and some basic financial markets history.
Learning Objectives
- Describe the implications and institutions associated with the short term interest rate, and describe how to compute single and compound interest.
- Identify the difference between coupon and discount bonds, and calculate the present discounted value of discount bonds.
- Determine the origin, the meaning and the valuation of two debt securities: consols and annuities.
- Understand the meaning of forward rates and to describe how to calculate them
- Define the meaning and how to calculate the market capitalization of a company.
- Explain the structure of corporations in the U.S. and the implications of owning shares in a company.
- Identify the differences between common and preferred stocks, and the concepts of dilution and dividends.
- Describe how and why companies repurchase their shares.
- Describe the basics of corporate governance.
- Further understand the pricing of stocks and the price-to-earnings ratio.
文章目录
- [Financial Markets](#Financial Markets)
- [Week 3](#Week 3)
-
-
- [Learning Objectives](#Learning Objectives)
-
- Lesson #8
-
- [1982 Savings Account](#1982 Savings Account)
- [Federal Funds and Interest Rates](#Federal Funds and Interest Rates)
- [Compound Interest](#Compound Interest)
- [Discount Bonds](#Discount Bonds)
- [Consol and Annuity](#Consol and Annuity)
- [Forward Rates and Expectation Theory](#Forward Rates and Expectation Theory)
- Inflation
- Leverage
- [Lesson #8 Quiz](#8 Quiz)
- Lesson #9
-
- [Market Capitalization by Country](#Market Capitalization by Country)
- [The Corporation](#The Corporation)
- [Shares and Dividends](#Shares and Dividends)
- [Common vs. Preferred](#Common vs. Preferred)
- [Corporate Charter](#Corporate Charter)
- [Corporations Raise Money](#Corporations Raise Money)
- Dilution
- [Share Repurchase](#Share Repurchase)
- [PDV of Expected Dividends](#PDV of Expected Dividends)
- [Why do firms pay dividends?](#Why do firms pay dividends?)
- [Lesson #9 Quiz](#9 Quiz)
- [Module 3 Honors Quiz](#Module 3 Honors Quiz)
- 后记
in the aftermath of: 在xxx之后
the situation in the aftermath of the financial crisis of 2008:2008年金融危机后的形势
passbook :存折
deposit:存钱
withdraw:取钱
you would present your passbook. And you could either deposit or withdraw. And they would enter your new balance in your passbook. 你应该出示你的存折。你可以存钱或取钱。他们会把你的新余额记入你的存折。
Compound Interest: 复利
coupon: 票息
maturity: 到期日
maturity of the bond:债券到期日
at par: 平价;按面值;根据票面价格
the coupon bonds which are more common, tend to be sold at par. 更常见的息票债券倾向于按面值出售。
Creditors:美 [k'redɪtəz] 债权人;债主;贷方;放款人;
impetus:美 [ˈɪmpɪtəs] 动力;原动力;推动;
board of directors: 董事会;理事会;
perpetuate:美 [pərˈpetʃueɪt] 延续;使永久化;使不朽;保持;
at discretion: 酌定;自行;随意
dividend is at discretion of firm,股息由公司决定
retained earnings:留存收益;保留盈利;未分配利润
expenditure:美 [ɪkˈspendɪtʃər] 花费;支出;开支;经费
capital expenditures: 资本支出
shares outstanding: 流通在外股票;净发股票
repurchase shares outstanding: 回购已发行股份
Lesson #8
1982 Savings Account

I wanted to start though with just
a little bit about the current situation, or the situation in the aftermath of
the financial crisis of 2008, 2009. And that's not what I'm showing you, this ad here, I found it from 1982. What I'm commenting here is that
the current economic situation is rather different from 1982, and one sign of
that is you don't see these ads anymore. [LAUGH] I was just thinking,
where are the ads for savings accounts? They used to be all the time in
newspapers and magazines and TV. So I couldn't remember what they
looked like, so I looked it up. I found this ad, and
this is one you'd love to see today, but you won't see it today. [LAUGH] So
this is offering a passbook plus account with a 7.4 per
annum interest rate.
Now say, do you even know what
a passbook savings account is? Actually, I have my passport here,
I think. No, I don't, it's in my other,
LAUGH\] it looks like a passport. You used to walk into banks, everything has changed so much. You used to walk in, and there would be a teller. And you would present your passbook. And you could either deposit or withdraw. And they would enter your new balance in your passbook. It's like a statement. Whenever you need money, you go right to the bank and you pull it out. Meanwhile, you're earning 7.4% interest per year interest on it. So this actually is an ad for somebody's passbook plus savings account, which has a term, it says this in the fine print. Stated term is three months. That means you technically, they might make you wait three months to get your money out. However, this is very similar to a passbook account because you make deposits and withdrawals without penalty or loss of earnings. In this case, though, you have to keep your remaining balance at least $1,500. So here you are. You can go in and out of this account whenever you like. So it's basically an overnight account, you can take it out any day, any hour. It pays a nice interest rate, and it's insured by the government, so there's absolutely no risk. So this is what you want, right? But you're not going to get it \[LAUGH
because it doesn't exist anymore. Now the secret is if you
want something like this, you're going to have to pay
a negative interest rate. Because it just doesn't pay. This business just doesn't
pay because interest rates at the short end have gotten very low. And I'm going to come back to this. We're talking about the term structure. The term of any contract is the time that
you have to keep your money in it and can't get it out. So this one is technically
a three month term. But they're saying, trust us,
you can get it out any time. So it's basically overnight, absolutely
no penalty for withdrawing, it says. So we are in a situation in which at the short term,
interest rates are virtually 0. It's a historic event. And so, when we talk about interest rates, we might wonder why these
things are happening.
Federal Funds and Interest Rates
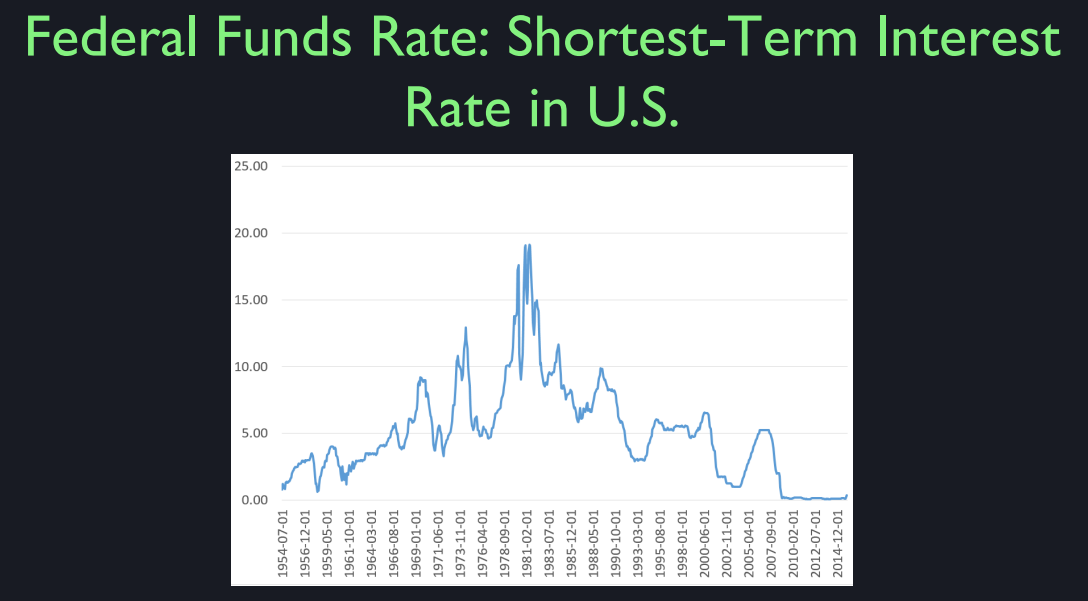
So this is the federal funds rate. Now, I'm mentioning term. Term is the time that you have to leave your money in and cannot get it out at least without a penalty. So this is the shortest term interest rate in the United States. It's called the Federal Funds Rate, and it's an overnight rate. Now, most of the people who deal in this maturity of one day are banks, because individuals normally don't borrow money overnight. It's too short an interval. Only people who are very sharp pencils and very professional will borrow money for one day. But it's a lively market, largely among bankers. So this is the interest rate on federal funds in the United States from 1954 to the present. So the ad that I showed you was from somewhere around here. I picked the high interest rate time looking for an ad. Those were different times. Look where we are now. This is amazing. It's right at zero. And it's been at zero ever since the crisis. Now, it's going to pick up. In fact, it's already picking up. Do you see this little uptick at the end? That was the decision of the government, the US Federal, well, The Federal Reserve under Janet Yellen to raise interest rates, and it got a lot of attention.
I have to say, I'm not very impressed by this raise of interest rates because it's virtually zero still. So something funny is going on here, wouldn't you say? If you looked at this whole, if your job was to predict interest rates and you were standing here in say 2004, would you have predicted this? Well, absolutely no. I shouldn't, say, there might have been someone who predicted this. But as far as I know, no one saw this coming but something very strange is happening. It'd be nice to understand this interest rate market. Now you might first of all say that well this is a targeted interest rate. The Federal Reserve announces a Federal Funds rate target, and they do everything they can and they've decided to put it at virtually zero. So you have to understand the Fed, but maybe you don't have to understand Janet Yellen or Ben Bernanke because these are the chairs of the of the Federal Reserve. Because anyone would do the same thing. It's an economic crisis that's brought equilibrium, short term interest rates down to zero. And to give you an idea that it is an economic crisis and it's not the personality of Janet Yellen that is accounts for this behavior.
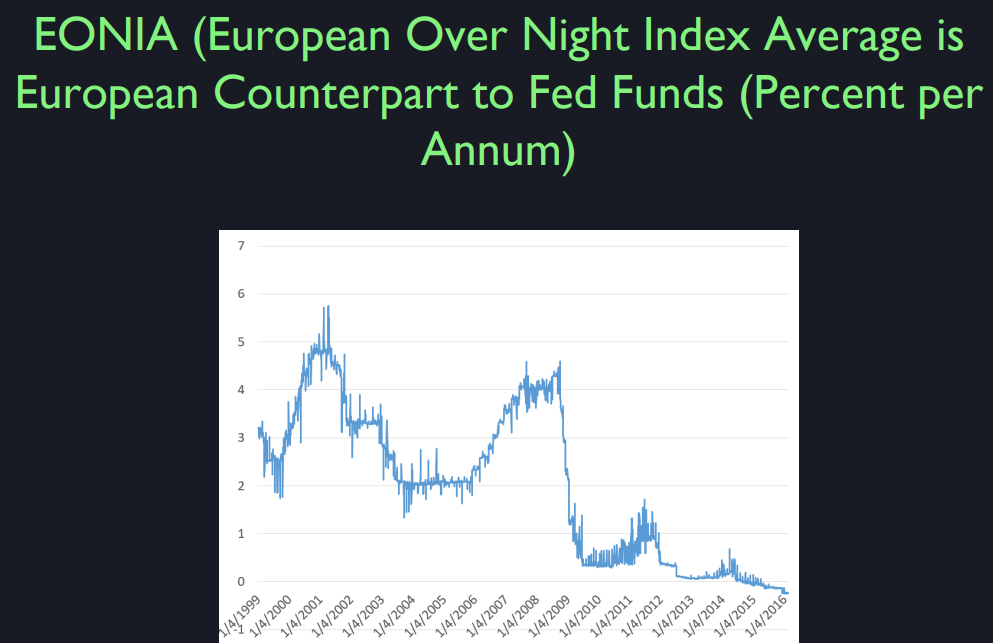
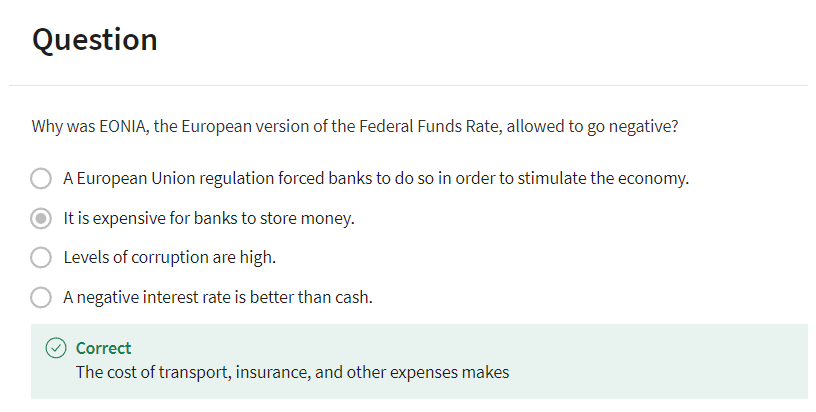
Let's look at Europe. So this is the European counterpart to the federal funds rate. It's called EONIA, European Overnight Index Average. So it's the same thing. Banks in Europe lend to each other overnight, and this is the interest rate. Now this only goes, I got these data from the European Central Bank and so that's why it only goes back to 1999. But you can see that it has the same downward path since 2000. Now, it's even more interesting because in the US, it stopped at zero. But it somehow knows no zero bound. In fact it's been negative for over a year. And it just seems to be trending down. Is this gonna... What is it... Now, if I asked you to forecast where it will be in 10 years, where will EONIA be in 10 years? Well, you might be inclined to forecast oh, I don't know -3%. Anyone believe that? Anyone offer a forecast? What do you think it will be? It can't go too far negative because the banks have the option of just holding on to cash. Why should we lend money at a negative interest rate? Well, that's an interesting question. You can blame Mario Draghi who's head of the European Central Bank, who he and the others at the bank have lowered the interest rate that they offer to European banks on deposits at the European Central Bank to a negative number.
So that you could say it was the decision of the Central Bank. But still it seems odd. Why does a bank ever invest money at a negative rate when they can just pull the money out and hold cash? Cash by definition, I mean real cash, paper money. Those those Euro notes that you have in your pocket, they pay exactly zero interest. So why would a bank lend to another bank at negative? Does anyone have an idea? Why would they? They are doing it right. We know they're doing it. Why are they lending to another bank at a negative rate? It's costly to store cash. First of all, if it becomes known that you have large amounts of cash in your vault, thieves might come and steal it, so you have to buy insurance against that. And then the insurance company will impose costs on you. Plus you have to hire those trucks to drive it. You know, it's not set up... Banks don't hold huge amounts of cash in their vaults. So yeah, so you've got to hire trucks and armed guards and it sounds... I think also it's just irregular, we don't do this. We don't have you billions in our vault. We have to get a bigger vault maybe because they don't. What's the biggest Euro note? It's probably like a hundred, does anyone know? 500. That's it 500. In the United States, it's only $100. So to store a billion dollars, you need a big vault. So you have to buy a new vault. It's silly things like that that allow negative interest rates. I think that as they learn that it's going to be harder to have a negative. So right now it looks like in this latest data shown here it looks like about -30 basis points where 30, a basis point is one hundredth of a percentage point. So it's minus a third of a percent. So they can get it lower than that for a while anyway. But anyway, it's just trying to understand why did it get so low.

So this brings us to causes of interest rates. There was a famous book written by Eugen Bohm von Bawerk in 1884, Capital and Interest, which said, "Interest rates tend to be small positive numbers like 3% or 5% because of technical progress, time preferences and advantages to round aboutness." I think he said round, he wrote in German so how do you say round aboutness in German? It's not exactly an English word either. I'll let you think about that. It's probably a translation of some long German word. But he said, why is it, and where does this number 3% come from? Why is it 3 percent or 5%? Well, he said, "It's because the rate of progress is something like 3%." Also so that sounds plausible, right. The economy is moving forward. So money, one dollar today is really if you take into account what will happen to the economy, it's really like a dollar, $1.03 and in a year. The other thing is time preferences. He said, "People are just naturally impatient. It's built into our, I don't think he said built into our neural structure, but maybe he meant that. So we just want more today. So if a dollar and three cents in a year is equivalent to a dollar today because I wouldn't... I prefer it now. And so I'll take a cut in what I have to get it now rather than later. And finally, advantages to round aboutness. That is advantages to more delayed and complicated production process. So for example, I can talk to... I'll just give you a very homely example. I can talk to a apple orchard and say, "How many apples can you give me today?" And so the guy quotes so many bushels of apples. And then you come back and say, "That's not enough, I want more apples." And he'll say, "Hey, you know our trees only produce so much." But you say, "I want more.". And then he said, "Well, okay, what I'll do instead of giving you apples now, I will sell my apples, buy fertilizer and I get stronger and bigger trees next year and I'll have more for you. But you have, more round about." Right. "I'm converting apples into fertilizer and I'm making the trees bigger. I can get you more next year." That's a roundabout production process. And so there's an advantage to that. So all three of those were causes of interest.
Do you think that low interest rates are contributing to inequality? There's definitely some connection because a lot of elderly people retire on fixed incomes. And if they have a rule that they will only consume the interest and the interest is zero, they're in big trouble. And that is unfortunately the situation. It's unfortunate that our efforts at policy can't help everybody. So monetary policy is a very blunt tool. You may feel that you have to cut interest rates to help the economy move ahead, but it doesn't affect everyone the same. And any time it doesn't, that, it has a potential to raise inequality.
Compound Interest

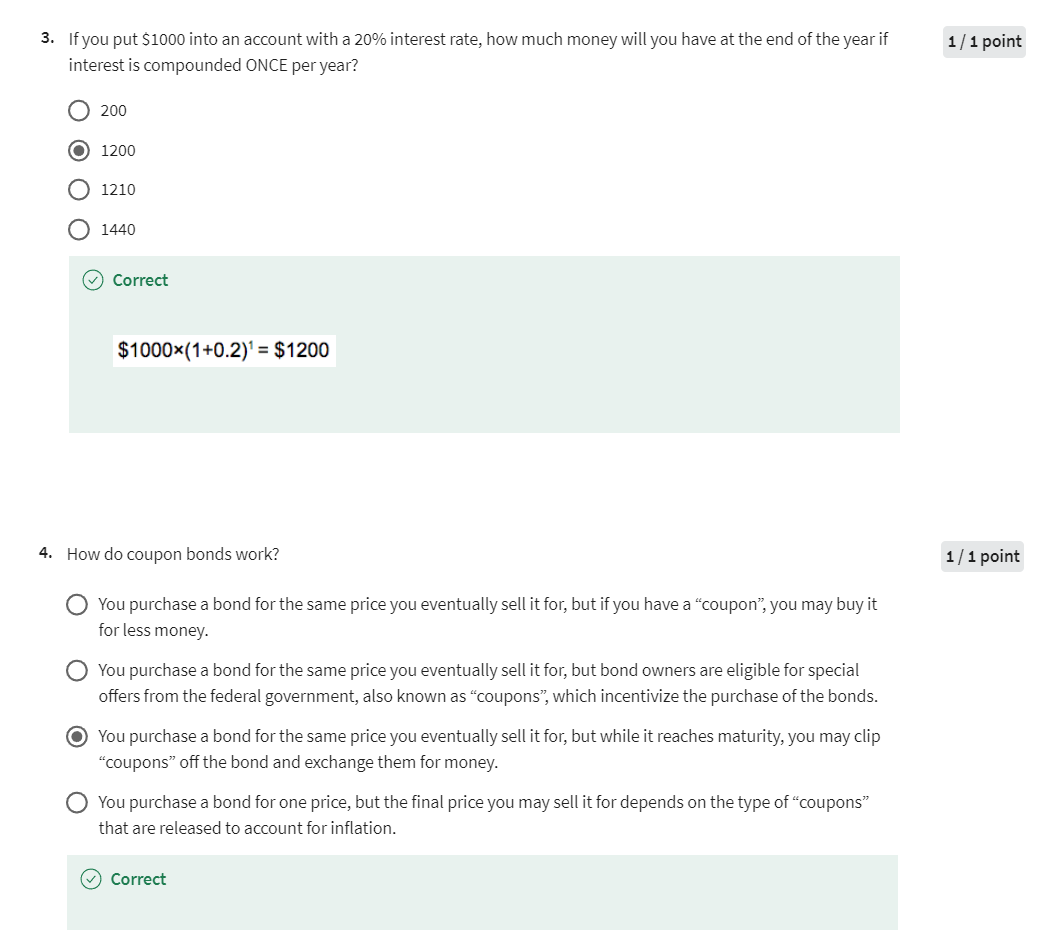
Now I wanted to give you a lesson, which,
I somehow have the impression you learned in high school,
did you learn compound interest? It's supposed to be such a basic math
point but let me just reiterate it. Suppose there's an annual rate of interest
r, and suppose that you're putting your money in a savings account in a bank
that promises to compound once per year. What does that mean? That means that your interest is
applied to the account once a year and you start earning interest on your
interest at the end of the year. So if I put $100 into an account
paying 3% compounding once a year, and
I go to the bank after six month and I say I'd like to cash out of my account,
what's it worth? They would say $100.00 because we haven't
credited your annual interest yet. So then you go [LAUGH] if you wait a full
year you can come back to the bank and now you get $103, now your account
is marked up for compounding. If you go back to the bank in 18
months since you deposited it, and you ask for your money,
they'd say well now you have $103 [LAUGH] because we haven't credited your
new interest for this year. You have to wait two years and
after two years how much do you have? You have 1.03 times 1.03, is little over 1.06,
if you have annual compounding. Now the banks often compound
more often than once a year so suppose they compound twice per year. You put in $100 in a 3% compounding twice
per year, if you went to get your money in the first six months,
you would still just get 100 back. After six months, you'd get 101.50, if you went back after nine months,
you'd get $101.50. You'd have to wait two years, no,
one full year, did I say that right? Yeah, you'd have to wait a full year and then you would get 1.015
squared times $100. You see where we're going on this,
if it's compounded twice per year the balance is 1 plus r
over 2 times 2t after t years. Where t is any number,
which is either one or, one plus, it's either an integer or an integer plus a half,
in between it's a step function. And if it's compounded n-times a year, the balance is one plus r
over n to the nt-th period. Now if you take the limit of this
expression as n goes to infinity, you get what's called
continuous compounding, and then the balance is e to the rt,
where e is the natural number. So if they continuously compound, it improves your interest
payments a little bit more, unless r is really big it's not, or t is
really big, it's not a huge difference.
Discount Bonds

Now, I wanted to find a discount bond. Bonds typically pay coupons. This is an old word but they still say coupons. It used to be, that if you invested in a corporate bond or a government bond it would be on a piece of paper they would give you. This is like for hundreds of years. And around the exterior of the pieces of paper, were little coupons that you would clip every six months typically. And you would clip your coupons every six months and take them to a bank, and the bank would then give you the money. So, each coupon would be so much money.
And then, at the end of the maturity of the bond, you could take the whole thing back and you get your amount back. So a typical bond back then, in 1900, and 1800, and 1700. Going way back. If you bought a 100-dollar bond, and it was issued for 100, and had say as a three-dollar coupon. Then, you would pay 100. You'd wait six months, you'd clip a coupon, and it would say, pay to the bearer one dollar and fifty cents. You'd go to the bank and get your one dollar and fifty cents. And you can see some of these bonds, they're framed and on display. Ones that defaulted, otherwise, the coupons would be already clipped and gone. You can see them, I think they're on displays on the fourth floor of this building.
A discount bond is a bond that carries no coupon. Now, why would you buy a bond that carries no coupon? How do you get interest from it? This is also time in memorial. People have traded discount bonds for a long time, and the answer is, because you buy it for less than 100. You buy it at a discount. So, they tend to be two different kinds of bonds, the coupon bonds which are more common, tend to be sold at par. You buy it initially for 100, and you sell it for a 100, you get back at the end when it matures after so many predefined years. With a discount bond, there are no coupons but of course, you buy it at a discount. There would be no other reason to buy it. Maybe today they're selling not at a discount with a negative interest rates. But normally, they're sold at a discount. We still call them discount bonds even there's a negative interest rate than they're selling for more than $100 initially.

So, if we look at the price of the discount bond, we can infer the yield to maturity from that bond. So, if someone says, I have a bond that will pay let's say, one dollar in T years, and it's compounding once a year, and the price I want is P, I can compute using this formula. What the yield to maturity is. So, I would basically take one over P, if solving this equation, I take one over P to the one over T power, and that's the yield to maturity. In a sense paying an interest rate of r, every year. Compounding once a year if I call it that. But typically, bonds pay interest rate every six months, that's the tradition. So, you might use this formula instead which has the bond compounding twice a year. If T is a number of years to maturity, and P is the price, then we will take P as the present value of the principal which I have as one dollar here, divided by one plus or over two, to the two T. So, the price today of the bond is called, the present value.
If it's a one dollar principal of one dollar at time capital T. And as a general rule, P is going to be less than one. I say is a general rule because it might not hold right now which is a little puzzling. But over most of history, it's a discount. P is less than one. So, is that clear? Any questions about that? You have to specify the compounding interval. But normally, for pedagogical purposes, it's convenient to take the compounding as once a year. And we just use this formula. By the way, you could do it continuously till you could say, what does that continuously compounded yield to maturity. And that we have P equals e to the minus r times capital T.
Okay. Now, we can define the present discounted value of any cash flow, not just a coupon flow which would be the case for a coupon bond, or the principal after T years for discount bond. Because we know that implicit in market prices for discount bonds, we can calculate the present discounted value of a dollar in any number of years. So, what is a dollar one year today? What is the present discounted value of that? It's one over one plus r, where r is the yield to maturity on a one year discount bond. And what is the present discounted value of a dollar in n years? It's one over one plus r to the nth power. Now, this is obvious to a banker who always thinks. When you talk money with a banker, and you're talking about money in future years, there's a little calculator going in his head, he has memorized the prices of all these discount bonds going out. And he's translating it into present value or present discounted value, PDV. Amateur's mess this up. Instead, they become vulnerable to fishes. Lots of people make mistakes. Maybe you should develop the habit of always computing the present discounted value. On the other hand, you live in a very good time for ignoring this. Because right now, interest rates are virtually zero. But it will come back. I think Nick you are right, we are going to have two percent and higher interest rates at some date in the future. I just don't know when. If you have a cash flow, x sub t, where x sub one is the money coming in in one year. x sub two is the money coming in in two years. And let's assume that the discount rate is the same for all these different maturity. This is a simplification. Then the present discounted value of the cash flow is the summation t equals one of the capital T, of the cash flow x sub t, divided by one plus r over the t. That's one of the most famous formulas in finance.

So, now let's look at a conventional coupon varying bond which is issued at par. How do they issue them at par by the way? It's tradition to issue at par because you're getting your interest in the form of coupons. What they have to do is judge the market. If I want to issue with par, what coupon is the market demanding on a 100? And once I know that, I'll just pick that coupon, and I can be pretty sure that my bond will be picked up for 100 because I've got the market coupon. So, I'm going to use c for the amount of coupon. Now, this is measured in currency, if we're dealing in dollars, c is so many dollars and the prices in so many dollars. And what it is now?
Now, here I have two versions. This is compounded annually, and this is the more realistic compound in every six months where t measures years. So, what you get in a simple case when you buy a coupon bond, is you get after one year, this is the annual compound after one year, I can clip a coupon for c dollars. And then, I have to wait another year, and then I can clip a coupon for c dollars again, and clip another coupon in three years for c dollars. And then at the end, I get my last coupon of c dollars, plus the principal which is a 100. So, I get 100 plus c dollars at the end. What is the present value of that if it's discounted at rate r? It turns out that's the formula for the present value. Now it's interesting to take the limit of this as t goes to infinity. If t goes to infinity, this term goes to zero, right? And this term goes to zero. So, we're left with c times one over r. So, that's the console. I think I have another slide for that. This is the more complicated formula for six-month compounding. This formula was sufficiently difficult that in the old days, and people didn't have calculators. Bankers would carry around the table, bond yield table. Also you can't solve this back. If I'm told the price of a bond, and I want to compute the yield to maturity r, I've got to solve this equation for r. And you can't. It's not algebraically possible. Unless, t is very small. So, you need a book. But now, it's probably already on your mobile phone. I think it is. I know it is. Go to Wolfram Alpha on your mobile phone and you'll get, or there must be other places. Must be hundreds of places that will solve this equation for you because it's standard. So many people think in terms of present values. And they want to know what the yield to maturity. What's the interest rate on a bond given its price.
Consol and Annuity

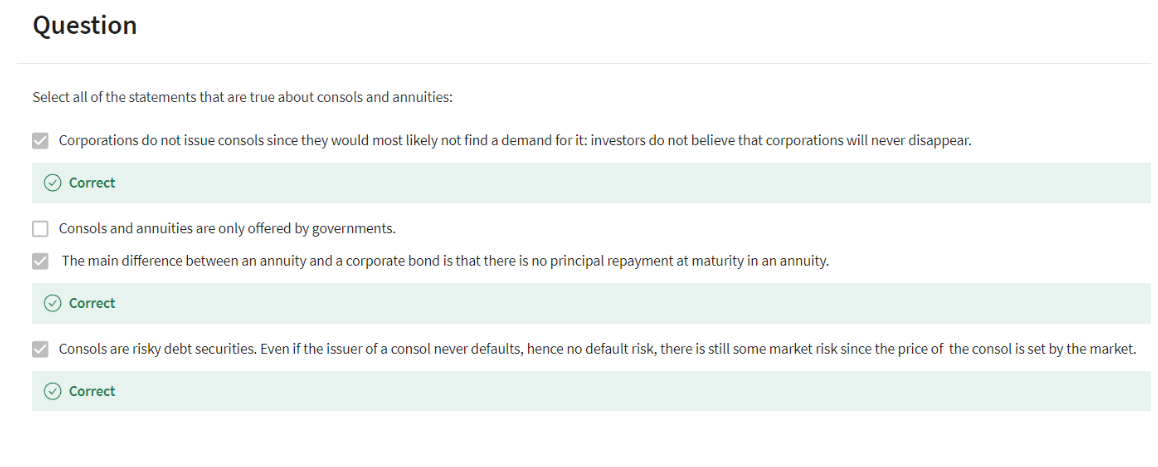
So I already mentioned a consol
is one that pays a quantity. What I was saying c or whatever x forever. And the consol present this kind of
value is x over or coupon over r. So it's kind of obvious in the case of a,
why do we call them consols by the way? Because in Britain,
in the 1700s, the government of the United Kingdom issued
bonds with no maturity date. They promised to pay this coupon forever,
and the only way they could get out
of it was by buying them back. And those bonds, well, there was
some adjustments made in the 1880s. They're still paying the coupon. The British government hasn't
defaulted in all that time. And so it's not forever,
but it's close to forever. I mean, several hundred years,
a long time to be paying a coupon.
在你提供的上下文中,"consol" 指的是由英国政府发行的一种没有到期日的政府债券。这些债券也被称为永久债券,最早在18世纪发行,并承诺无限期支付固定的利息。唯一能停止支付这些利息的方式是政府回购这些债券。
"consol" 是 "consolidated annuities" 的简称,反映了这些债券合并了早期的债务。consol 的主要特征包括:
- 永续性:它们无限期支付利息(或至少支付非常长的时间,如几百年)。
- 固定利息:利息支付是固定和定期的。
- 无到期日:与典型债券不同,consol 没有固定的还本日期。
consol 的现值可以用公式 ( \frac{x}{r} ) 计算,其中 ( x ) 是年利息支付,( r ) 是利率。这个公式反映了收到固定支付的永续价值由支付金额除以利率决定。
In the context you provided, a "consol" refers to a type of government bond issued by the United Kingdom that has no maturity date. These bonds, also known as perpetual bonds, were first issued in the 1700s and promise to pay a fixed coupon (interest payment) indefinitely. The only way the government can stop making these payments is by buying back the bonds.
The term "consol" is short for "consolidated annuities," reflecting the way these bonds consolidated earlier debt. The key characteristics of consols are:
- Perpetuity: They pay a coupon forever (or at least for a very long time, such as several hundred years).
- Fixed Coupon: The interest payments are fixed and regular.
- No Maturity Date: Unlike typical bonds, consols do not have a set date when the principal must be repaid.
The present value of a consol can be calculated using the formula ( \frac{x}{r} ), where ( x ) is the annual coupon payment and ( r ) is the interest rate. This formula reflects the idea that the value of receiving a fixed payment forever is determined by the payment amount divided by the interest rate.
Now it's simple to understand
the consol present that says the price of the consol
p is equal to c over r. You can just return that, turn it around. It says the yield to maturity
on a consol is c over p, and that's kind of obvious, right? If the consol is paying a 3 pound coupon,
and it's selling for 200 pounds,
I say what is the yield to maturity on it? Well it's 3 pounds divided by 200 pounds. In that case it would be, if it was
3% yield to maturity, I'm sorry if it was a 3% coupon issued,
it's now paying one and a half percent yield to maturity
because the price has gone up. This is an important point with bonds. The coupon is fixed at the time
the bond is issued but the market price of the bond
changes through time so if the British government
issued a 3 pound consol for 100 pounds and
that consol is selling for £200 today, the yield to maturity is
down to 1.5% instead of 3%. But this is no fault of the British
government, they are true to their word. They are paying the consol as promised,
it's the market that does it so bonds are risky, they have market risk
even if there is no default risk. If you buy a consol,
you know you won't live forever. The British government may
live forever but you won't, so you're going to want to sell
the coupon at some point. The British government does not
guarantee the rate that you will get, the price you will get for
selling your consol. So, there's market risk for
our consol and for any debt instrument,
long term debt instrument. By the way, if a bank or a company or a government were to issue
a usually companies don't issue consols because nobody
believes they'll last forever. Patriots in Britain might believe that
the British government will last forever. Although I can tell you it won't [LAUGH],
not forever. Nothing is forever. But they imagine it's forever, so
they're willing to buy British consols.
But what if the British government
did something even more dramatic? They say, we're going to have the coupon
on the Consol growing at a constant rate. So, it's going to start out at 3 pounds,
and then it's going to grow
at a rate g per year. G is a percent of growth per year forever. Well what is the present
value of an amount x if the rate is the yield to maturity or interest rate is r and
the x is going to grow at rate g? Well, it turns out the growing consol
present discounted value is x over r minus g. So, by the way, what happens if g is
greater than r [LAUGH] or g equals r? Any idea on that? Well, I think you probably
can figure this out. It's, if g equals r it's x divided by 0,
it's infinite. That's because it's the series that
you're summing is not convergent. If you're getting an amount that's
growing at the rate of interest, the present value is infinite and if it's growing at greater than the rate
of interest, well the formula breaks down. It's still infinite. So that's why we get puzzled
about the present situation. If the interest rate is 0 then
consols don't even converge. How can that be? Doesn't the interest rate always
have to be above the growth rate. How can anything,
nothing can have an infinite price. Well, I guess the answer is short
term interest rates have 0 but longer term interest rates
are still positive so and the US doesn't have consols, but we have something analogous to consols,
like land, for example. That lasts forever, as far as we know. You can rent it out or you can plant
crops on it, as far as we know, forever. Maybe those crop, what about land? Aren't crop values rising through time? So that g is a positive number? And if interest rates are,
they can't be 0, they have to be, bond rates have to be above
0 otherwise assets that have growing payments would be
worth an infinite amount.
Now this is an annuity
present discounted value. Now an annuity is like
a consol except that it stops after a certain number of years. In a typical annuity,
a typical annuity is a home mortgage. When you buy a house,
the typical financing you'll get, is that you will pay now
the compounding integral is monthly. They think it's not realistic
to ask ordinary people to pay their mortgage every six months
because it's too hard for them. They'd have to,
they wouldn't remember to save and they wouldn't have enough
money to pay after six months. So we gotta move to a monthly schedule for
individuals. A typical and that's not,
this is not compounding monthly. This is the present value
of X dollars every year, starting in one year and
then again in two years, then again in three years and
the last payment is T years. This is different from the present
value for a corporate bond, or for a coupon carrying bond because there's
no principle repayment at the end. I'm talking about,
I think I have another slide on mortgages. I'll come back to that. But I tell you realistically, these financial instruments are designed
around human imperfections. People find it difficult
to pay back a mortgage. And what they'll find
especially difficult, is to pay a balloon payment at the,
they call it a balloon payment. There used to be mortgages like this. You would borrow to buy your house, you
would say, I'm going back to the 1920s. The house cost $10,000,
typical house in the 1920s. You borrowed 9,000. You've got your own money to put up. The 9,000, then you pay back
the money at a rate interest. And then, but at the end, you don't owe
anything except the last monthly payment. So that's what an annuity is.

This is a little history of thought,
actually the Growing Consol Formula has been
called the Gordon Rule according to Myron Gordon who was a professor of
economics about a half century ago. But actually it goes
back to Jacob Bernoulli, I learned that from Will Goetzmann and
his co author Geert Rouwenhorst here. So it's an old formula
Forward Rates and Expectation Theory

Forward rates are interest rates that can be taken in advance using the term structure. I was writing an article about the term structure of interest rates and I was wondering, "Who invented the concept of forward rate?" And I couldn't figure it out. It's hard to find the first especially back when I was writing when we didn't have the internet. I asked a graduate student, "Can you find out who invented the concept of forward rate? I think it's Sir John Hicks.". So my graduate student went to the library, -the way we used to do these things- and tried to find out. Then he came back to me and he said, "You know, Sir John Hicks is still alive, you could ask Him." So I thought, "I never thought of that. Is he still alive?" So this is back. I don't know like 1980 or something. So I thought, "All right, I'll find his address and I'll mail him a letter." So I typed a letter to him saying, "Did you invent the concept of forward rates?" And I waited about six months and then I get a letter back handwritten with shaky handwriting and so John Hicks said, "Interesting question. Did I invent that concept?" He had shaky handwriting, "I apologize, my health is not good anymore, but I thought I would answer your question." So he went back and he said, "Well, I thought it was, I did a trans- my wife and I did a translation around 1920 of a book by a Swedish economist. I thought it was there, but I went and it's not there." And then he said, he reminisced about conversations he had at coffee hour at the London School of Economics in the 1920s and he said, "Well, maybe somebody brought this up, but I don't know. Maybe I didn't read it." So I put my example here at the coffee hour at the London School of Economics. The year is 1925. This assumes that he got it from some verbal conversation but nobody knows. He's long gone now, we can't ask him again. So here we are sitting at the London School of Economics in 1925 and somebody is saying, "I'm wondering what interest rates I can invest money at in 1926?" That's next year. Remember you got to put yourself back in the time machine here.

So the year is 1925 and you want to invest the money between 1926 and 1927. And he said, "I just wonder what interest rate I can get in 1926?" That's a year in the future. But apparently somebody maybe it was Sir John Hicks at the coffee hour said, "That's a dumb question." Maybe he wasn't so rude. He said, "I can get it today. I can lock it in today." This is 1925, but there's already an interest rate between 1926 and 1927. So we'll call that the forward rate, but that term hadn't been invented. It's amazing how simple concepts don't seem to be known until somebody points them out aggressively. So this is the coffee hour conversation as I'm reconstructing it. This is how you do it.
How do I lock in an interest rate as an investor from 1926 to 1927? I buy in 1925, this number of two-period discount bonds maturing at 100 pounds in 1927. They are two-year bonds. The cost- okay. So, I'm buying this number of them. So if I'm buying this number of them, the cost to me is one pound over one plus r one. And then I have to short in 1925 one- one period discount bond maturing at $100 in 1926. So I receive one over one plus r one pounds. Now think about it. I have locked in an interest rate equal one plus F which is equal to one plus this two- period yield-to-maturity squared all over one plus the one period you have to maturity. And I've locked it in. So this was kind of a showstopper at the coffee hour at the LLC in 1925. This guy thought he was answering unanswerable question and here it is. So that you could pick up today's copy of the London Times and these prices of discount bonds will be listed. I can tell you exactly what the market today is quoting for the 1926 to 1927 investment. So is that- is that clear? It's a little tricky I guess nobody thought to talk in those terms until then.

Inflation

I was doing the introduction for the John Bates Clark Medal at
the American Economic Association. And I was telling our own members at
the AEA what did John Bates Clark do that is most distinctive. In 1895,
he wrote a journal article defining what he called the real interest rate. What it is, is the interest
rate corrected for inflation. Now, I did a search to see if anyone
knew of real interest rates before 1895. And I got hits in 1894 and
1893, but nothing before that. So I think it was John Bates Clark
who invented the idea. It's just amazing to me that people
didn't understand forward rates, they didn't understand real rates. To me they seem like
such natural concepts.
So the nominal interest rate, what we've been talking about now,
is quoted in currency. Dollars, Pounds, Renminbi, whatever. But it's not corrected for inflation, and as you know when you have inflation,
the value of the currency declines. The real rate is quoted in
terms of the market basket that underlies the price index,
consumer price index. So just in simple terms,
if you are investing money at 3% for next year and the inflation rate,
consumer price index, is going up at 3% what is your real rate? How much are you making in real terms? Well, it's kind of obvious,
it's zero, right? If I have 3 more on my 100 investment,
but everything that I want to buy has gone up
by 3% then I have the same buying power. So I didn't get anything. So the simple way of describing it is
usually the real rate, this is simplified, the real rate equals the nominal
rate minus the rate of inflation. But actually the formula
is more like this. One plus the nominal rate, or money rate, equals one plus the real rate,
times one plus the rate of inflation. This is an approximation. If you multiply this through, you'll see
that it's missing the cross-product term, the product of R money times I. Which is close to zero.

Another really important invention in
history is the invention of index bonds, which are bonds that pay coupons
defined in real terms and a principle, or one or
the other in real terms. In 1780, I'm attributing
this idea to Paul Revere but I don't know it probably wasn't his idea. But he engraved the bonds,
the first issue of index bonds. I bought one under
Will Goetzmann's influence. I discovered,
I could buy one of these bonds. It'll only cost me $1,000,
and I have it up and it's framed in my office if you
want to come back and see it. Engraved by Paul Revere,
that's pretty neat. But what's even neater about it,
was it was a clever idea. Let's issue bonds whose coupons
are just tied to the inflation rate, so that you know in real
terms what you're getting. The US Treasury did not follow
up on Massachusetts until 1997. So that's 217 year lag between the first issue of indexed bonds in
the United States, and the second. Well, there might have been some minor
issues somewhere in between, but basically that's what happened. So they were called TIPS, they still are,
Treasury Inflation Protection Securities. They were issued in 1997. By 2006,
they were 7% of the national debt. I should update this. They went up more by 2010 or so. I think they're down now. But, they're still big. In the UK they call them
index-linked guilds. They're bigger in the UK, by 2006 they
were 25% of the UK National debt. And France and
other countries have been issuing them. They're still a little controversial,
but they make great sense to me.
Leverage

If a company or
an individual borrows money to buy assets, we say that person or
company is leveraging. Leveraging means you are putting more
money into the asset than you have. You could buy, if you have $100 to
invest you could buy 100 of stocks, or you could buy 200 of stocks and
borrow $100. That makes you in a riskier situation,
but also both up and down. So if you bought $100 worth of stocks and
you're lucky and it doubles in value to $200,
you've made $100. But if you leveraged and
the stock doubles in value, your portfolio goes from 200 minus
100 to 400 minus 100, or $300. So you double your profits. But on the other side of it is
if the stock falls in value. Suppose you bought it unleveraged. You bought $100 worth of stock and
it falls in value by 50%, then you are down to $50, you've lost 50. But if you leveraged and
you borrowed 200 worth of stock and borrowed 100,
then if it falls by 50% you're wiped out. So leveraging increases risks. People look at how
leveraged economies are and wonder about the chaos that might
ensue in a market correction.
For example, China is widely described as a highly leveraged country, it's
gotten worse after the financial crisis. There was a Wall Street Journal article
just the other day pointing out that corporate debt,
borrowing by corporations in China. It is 160% of GDP in China. Whereas in the US, it's only 70%. So that means the Chinese
economy is leveraged. And it could do very well
as a leveraged economy, but it's more vulnerable and
this is a concern. So debt leads to bankruptcy. If you have no debt,
you normally don't go bankrupt because bankruptcy occurs when
your creditors are after you for non-payment and normally, you would
just pay them if you had the money. It's just when you don't have
the money that you are in trouble.

Now I think a very important,
I keep coming back to Irving Fisher. As I say, I'm a little bit biased
because he's a Yale person but I never even met the guy and
I don't know if I would like him. He's kind of a quirky guy. He would invite students over for
dinner at his house, and he would tell them at dinner, you have to chew each bite
100 times before you swallow. Because he thought that was health. Anyone do that? [LAUGH] Be careful to chew your food well? It must have been a little bit odd
having dinner with Irving Fisher. But he was a brilliant economist and he wrote an article in 1933,
in Econometrica, called the Debt-Deflation Model
of Great Depressions. In 1933, prices were falling at a rapid
rate because of the depression. We had huge deflation. And he thought maybe that's why
we are having the depression, and here's his train of thought
as he describes it there. Normally people who borrow
money are the optimists, right? They're borrowing, they're leveraging. They think the stock market will go up or
some other market will go up and they want to get it. And they're willing to take risks. So you have the risk-taking optimists on
one side and then you have the naysayers. They are people who are pessimistic and
risk-averse and they don't want to take
chances as the lenders.
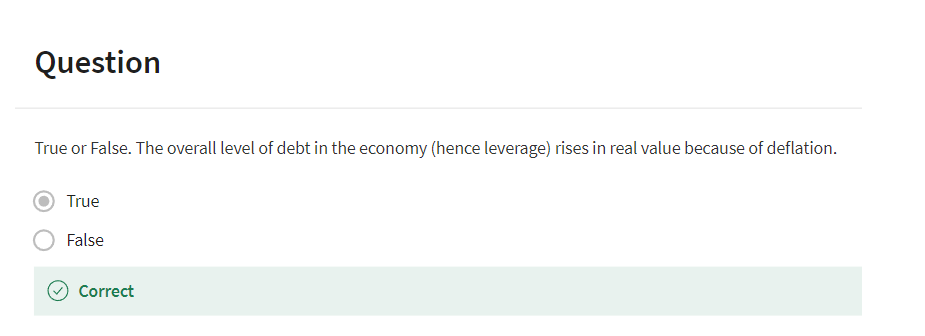
So, what happens when
there's a huge deflation and consumer price index goes down? Well, that magnifies the real
value of the debt, right? If you owe $100 and
the consumer price index falls by 25%, your debt has gone up to about 133,
it's gone up a lot. So what ends up happening in a deflation is that the debtors get beaten down. The optimists have less
wealth in real terms and the pessimists have more because now the
$100 that they loaned is worth a lot more. So he thought this has to be important. You know that people are different. Some people are natural optimist, and
some people are just, not necessarily that they're just pessimistic, but
they just don't want to get into that. They're not entrepreneurial. I don't mean that disparagingly. They're just a different personality. Maybe they're artistic or something else. But then in a depression,
wealth gets distributed towards them so in a weighted sense they
get more votes now. So you've now rewarded the pessimists and
the world is being run by the pessimists. So no wonder we're in
a depression in 1933. Now the recent crisis, that is of 2008/9. That's no quite so recent anymore,
but it's still with us. Did not bring much deflation,
not like 1933. But what it did do is it produced lower
consumer prices than people expected. because inflation often
practically disappeared, and there was some deflation at times. So that means that irrelative to
expectations, wealth had been distributed, redistributed from those who borrowed
money to those who lent money. So it's still true and
it may be important factor to consider. This brings up a question
that I've already alluded to.
Why isn't debt indexed to inflation? Well it isn't. This is the puzzling thing about human
nature, people just don't get it. And it happens again and again that we
have major shifts in the price level and it redistributes debt value
between debtors and creditors. People just don't get it,
I think they're afraid of index numbers, this calculations,
the consumer price index, there's some calculation,
you want my debt to be tied to a formula. So anyway I've already alluded to the fact
that I think we should create an indexed unit of account like they have in Chile or
Mexico or some other countries. So that it would be easier for
people to contemplate indexation, but they dont, this is the real world.

So any time we see unexpected
behaviour of consumer prices it has real effects on the economy. John Geanakoplos here at Yale has written a number of papers
on what he calls the Leverage Cycle. And pointing out that leverage has
varied quite a bit through time, notably recently in
the United States in 2006, just before the financial crisis. Leverage became extremely high,
particularly in the housing market. Banks were allowing people to borrow, typically something like 97% of the value
of the house, to borrow a house. So this leverage, you think anyone
who takes a risky investment and borrows 97% of the money,
that's really a daring thing to do. But everyone was doing that. Anyone who was in that stage of
the lifecycle where you'd buy a house, it's funny how people value, I don't think that people are consistent
at all in their thinking about risk. A view developed in 2006 that the housing
prices are going up, I said before 2006. Housing prices are going up so fast you
can make a lot of money by, in fact you could make a huge amount of money,
percentage-wise, by just buying a house. If you bought a house in 2000,
home prices went up, well, I don't know, I should have this memorized, but
let's say they went up 50% after that, you make 50% on your investment,
it's pretty good. But if you borrow 97% of the money, it's
just astronomical what you could make. People got excited about
leverage because they also had the perception that
home prices don't fall. I know this was out there,
people had this idea. Why do they think that
home prices don't fall? Just the Law of Economics,
house prices never fall? But we know the law is wrong because
in 1933 they were falling rapidly and so, I guess that's beyond
people's memories. So, people got kind of an optimistic
bias just before the financial crisis. And the economy leveraged itself up. It isn't the government that did it. The government if anything,
was leaning against that with regulations. So anyway, so
that's the end of my thoughts. So is debt immoral? I tend not to think of
it at all as immoral. We talked about the Irving Fisher diagram. How the ability to borrow and
lend raises utility. I think that at various times
in life you need money, the extreme case is you need money for
illness, you're sick, you're going to die,
you need expensive treatment. Of course you borrow the money. So lenders are not evil. Even if they lend, we talked about this,
even if they lend for your honeymoon, for a vacation. That's not evil, either. You may know, psychologically, your fiancee needs that if you
want the marriage to succeed. And that's just something you have to do. It's not crazy, it's not self-indulgent. So I think debt is a good thing,
but not always well-managed.
The overall level of debt in the economy (hence leverage) rises in real value because of deflation.
Lesson #8 Quiz

Lesson #9
Market Capitalization by Country
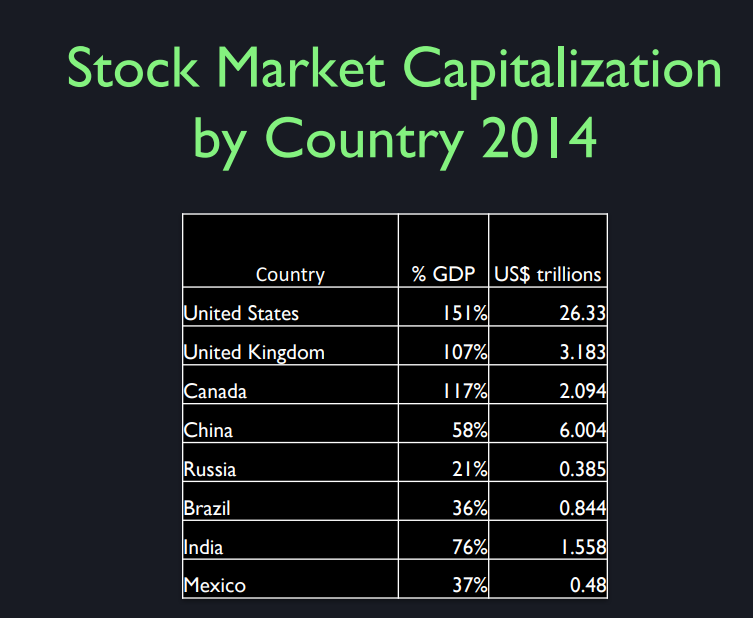
Now, we did not invent stocks
in the United States of America. I wanted to show market capitalization. Remember, we defined that market
capitalization is the price per share multiplied by the number of shares,
and this is common stock. I'll define that in a minute. I just took some,
kind of the latest year I could get data, shows the market cap in trillions
of US dollars by country. Just for a random selection
of countries that I picked. And here is the market cap
as a percent of annual GDP. So the United States leads the pack,
for now. United States did not invent corporate
stock, although it was here in the United States that a general
limited liability law was invented. And that may be a head start that this
country got to impetus towards huge stock market valuation. But as of 2014, the market capitalization
of the US stock market was 26 trillion. Actually, it hasn't changed a whole lot
since then, because 2014 was a peak. 2015 was flat, 2016 is down so far, so it's something like that now,
at 151% of GDP. No other country comes close, but
I think if you put the EU together, I didn't do that, that's the European
Union, it comes somewhat close. Here's one EU country. The stock market as a percent of GDP is lower than the US, but
they have a very large GDP. Canada is a little bit less capitalist. See, we're really
capitalists in this country. We have a big stock market,
it's all traded. A lot of this isn't owned
by Americans by the way. The Chinese love the US stock market and
they would invest in it more if there weren't regulations in
China making that difficult. But America is for sale, but I should add,
the US Stock Market is not America. It's a particular thing,
it's a particular contract. It's a claim on earnings
of the corporate sector. And there's much more to this country, and
to any country, than the stock market. So I don't want to overplay it.

Okay, just to give another perspective,
this is now about the United States. The Federal Reserve Board of Governors has a balance sheet for
households and non profits. They lump in non profits with households,
which I think is unfortunate, but they're small, it's basically households. So what's the total wealth tangible? We're not including human capital. You can compute a present
value of your lifetime income. For each of you, that would be in
the many millions, I'm hoping. [LAUGH] Not for each of you,
some of you won't do that. [LAUGH] But most of you, because you'll
live a long time and earn money for a long time. But what is the tangible assets that we
can quantify and value through markets? According to the Federal Reserve,
as of 2014, these assets were worth $98 trillion US. It asks people to add up everything
they own, their house, their stocks, their bonds, everything. Add that number for every household,
and you get almost $100 trillion. But people don't own it free and
clear, they have liabilities. For example, typically they borrowed money
to buy the house, so they have debt. So we want to subtract
off those liabilities. The total value of those liabilities
in 2014 was 14 trillion. So that leaves the total
net worth of households in the United States at 84 trillion.
That's quite a bit more
than the stock market. Now corporate equities own directly,
now equities, that's the same as stock, common stock. Households own directly 13.9 trillion,
that's less than half of the stock market. They tended to own it in other
forms like mutual funds which are, as of 2014, were almost 8 trillion. What are mutual funds? They are collections of investments
made by a investment company, who then sell shares to the public. Now this includes, I believe, other,
not just corporate stocks, but also it definitely includes bonds and other
investments that mutual funds might make. But it's mostly stocks, and
pension funds, 20.6 trillion. Those are investment companies
that save for your retirement. Your employer typically gives you one. This is not social security, social
security is a government pension fund. But companies also, as a compensation to
their employees, give them pension funds. And the pension funds invest and
typically buy stocks. Now you'ill note that these numbers
add up to more than 26 trillion, which is my market cap for
the stock market. But that's because pension funds also
invest in bonds and other things. And then the balance sheet for the Table
B101 also includes the value of real estate owned directly by households,
that's mostly single family homes. It also includes vacation homes, some
households have investment properties, so the total value of real
estate owned by household. Then I have to say in parentheses,
and non profits is 23.7 trillion. Bigger than the stock market? No, not quite. Bigger than the direct holdings on
the stock market, close to twice as big. So even in America most people are not
that into stock market investing. I think it might be very smart policy
not to buy a home, to rent a home and invest in a broadly diversified portfolio
which that should be less risky. But most people don't do that,
and maybe they have good reasons.
The Corporation

So what is a stock? Well, we first have to think
about the corporation. So the word corporation comes from
the Latin word corpus, meaning body. And what it is,
is an organization that is. Incorporated, that means it's made as
if it has a body, as if it's a person. In fact, the word person in law
typically includes corporations. If you wanted to say an individual
you could say a natural person. [LAUGH] A corporation is
an artificial person. The idea is to create
something that legally has a lot of the rights that individuals do. And traditionally it would be created
by a royal charter, prescription, or act of legislature. More recently it's done according to
procedures that are widely available. In Ancient Rome they had corporations,
they were called publicani. But they were limited, and
they had a stock market. This is what you can read
in the Goetzmann book. The stock market of
Ancient Rome was outdoors on the street in front of one of
the temples in the Roman Forum. And you could go and
buy shares in company. There isn't much data left
about stock prices then. Most of the companies, at least later
in Ancient Rome were of a certain kind. They were tax collectors. The Roman government paid private
companies to collect taxes for them. Why not, right? It's not the way we
normally do things today. But rather than go out after everyone, the
government just hired a company to do it. And those were traded
on the stock exchange. They didn't develop much. I don't know the reason. They didn't have any insurance
companies or shipping companies. Those kinds of activities were
done without incorporation.

Now let's talk about a modern corporation. The modern corporation in
the United States let's talk about a for-profit company like those that
are on the New York Stock Exchange. It's governed by a board of directors
that is elected by the shareholders. So it's called shareholder democracy. Typically one share, one vote. So it sounds like a sensible thing. It's a little bit like
the electoral college in U.S. Constitution for the government. You vote for electors and
then the electors vote for the president. Similarly, you as a shareholder
vote your shares, one share one vote in a company sounds
sensible to elect the board of directors. And then the board of directors
votes on who will be the president. The CEO or president, we now tend to
say CEO, chief executive officer. And companies will also have a president. But the CEO is generally the top,
for instance. So the person, the CEO is hired by
the board, serves as an employee, and has to report to the board of directors. Even non-profits are somewhat like,
they do have a board of directors. And then they hire the president. And there are other structures in Germany,
notably, a company will have two boards,
an Aufsichtsrat and a Vorstand. The Aufsichtsrat is a supervisory board which stands on top of
the whole operation. The Vorstand does the details, manages. Well, it doesn't actually,
it hires people to manage the company. But it's in charge of
day-to-day activities. But it's the same basic idea,
they just divide it into two parts.

Now I've been talking about
for-profit corporations, we also have non-profit corporations. A for-profit corporation is
owned by the shareholders and the shareholders have one vote each. The shareholders have the claim on
the earnings of the company, and have to pay a corporate profits tax. The company has to pay a tax to
the government on its earnings. Non-profit corporations, for example,
Yale University are not owned by anyone. Now you might ask, how can that be? How can it not be owned by anyone? Well, they have a board of directors
called the Yale Corporation. And they have a prevision
where alumni can elect them. Other non-profits would
just be self-perpetuating. That is the directors
appoint their own successors. It sounds a little wild,
because what if the directors get crazy? Then the whole thing could
go down in craziness. But that's the way we leave it. Generally it works. Generally the board appoints other
people who have normally some idealistic commitment to the purposes
of the non-profit. The for-profit exists for shareholders. The non-profit exists for whatever the charter of the non-profit
says, it promotes some cause. For-profits have a price per share. Non-profits are not traded and so they
don't have a price, no price for them.
You mention non-profit
organizations in your lecture, so can you talk about, does non-profit
status means that their revenues should never exceed their costs
to maintain a non-profit status? >> Yeah, non-profit,
maybe it's misleading. It doesn't mean that
they don't make profits. It means that they don't distribute
profits to shareholders. The purpose is not to distribute profits. But they do have a purpose. In a for-profit company, the objectives that are focused on are the shareholders. They take the money and
they do what they want with it. But in a non-profit, the non-profit can
make as much profits as it wants but it keeps them in the company and
spends them on some purpose. A non-profit has to be
defined with a purpose. Because it is doesn't go, otherwise they
would just sit on the money forever. And, in fact,
that kind of thing has happened where non-profits accumulate
huge amounts of money. And people wonder, where's it going to go? Where's it going to be spent? Sometimes non-profits are developed
that have a goal that gets lost later. One famous example is the Shaker Church. That was a Christian church
in the 19th century and they created a foundation and
they accumulated money. But there aren't hardly any Shakers left,
there might be two left in the world. And so the foundation is being
run by people who have to think, well what would I do if I were a Shaker? That is a potential
problem with non-profits. But usually they're defined with
a purpose that will endure and will continue to motivate
their use of the profits.
Shares and Dividends

So now I want to make a very basic
point about corporations and shares. If I give you 1,000 shares
in a company and you wonder, what does that mean that
I own 1,000 shares? You have to ask another question which is,
how many shares at there had standing? So we talked about this before. I'm not up to date on this but it might share of the company is
equal to the total number of shares I own divided by the total number of
shares outstanding for the company. So it's my number
relative to the tutorial. If I own half of the shares outstanding
then I own half of the company. Companies do things called splits
where they will break a share in 2, and call one share another 1.5 shares or
2 shares or whatever. They do that periodically. Why do they do that? It seems that companies think that
there's an optimal price per share that encourages investors look right,
feels right. And so they will change the number
of shares from time to time to try to hit a target for
the price per share. In the United States, by tradition, the target price per share is
something like $30 a share. So suppose your company
has done very well and the price per share which was
originally 30 is now up to 60. Your board of directors may then, someone might bring it up at the board
meeting, we should do a two-for-one split to get our share price back
down to the magic $30 a share. So then you would then send out a letter
to all of your shareholders and saying, we're doubling
the number of shares, and by the way this year, you now have
twice whatever you did before.
Well, I put down my slides. This is essentially meaningless. Other doing is changing
the unit of measurement, it's like going between [FOREIGN] and
FOREIGN\]. It means nothing. By the way they even do it. Well, why not? One reason they do it is they just think if the share price gets too high, you can't buy a fraction of the share. It gets to expensive, and people like to buy in round lots because the brokers encourage that. About 100 shares. So if it's $30 a share, you can buy an investment round lot for $3,000. But it gets expensive if you don't split. Now one company that doesn't split is Berkshire Hathaway. That's Warren Buffet's company. And it's been selling for thousands of dollars per share. So you can't even buy a round lot unless you a substantially wealthy person. Warren Buffet does that out of some principle. He can do it. Or I should say, his board does that. They can do it because it's all meaningless. But not totally meaningless just that it gets hard device small amount of share. You can buy one share but you can't buy a half of share. So now the company is defined as I said in basic terms, by a board of directors. The company has a constitution, called the Corporate Charter, and the Corporate Charter defines how things are done, but the general principle is guided by state laws. It's state governments that manage. You have to incorporate in a state, which means you choose a state to make your headquarters in. And that state then restricts what you can put into the corporate charter. Delaware is the most popular state for incorporating, because, well, it's the smallest state in the United States and smallest states have an incentive to be very generous to corporations, and they will all move to your state and you end up making money. Big states wouldn't do that because they already have corporations we need to be there. So the corporate law in the state defines the rights and responsibilities of shareholders and the board of directors. Well, it might say something about dividends but it doesn't tell the company what to pay out. This is something that's often forgotten. You buy shares in a company to get dividends. \[SOUND\] A dividend is a distribution of money from the company's earnings to its shareholders. \[SOUND
That's why, in America at least, especially, we're very clear. Why would you buy share in a company? Hey, they pay dividends. It's like interest except its variable. And tends to grow through time. Whereas, debt contracts doesn't grow,
it's just fixed. So you're doing it for the dividends. Remember we had the return on
a corporation has two components, the capital gains which is the
appreciation in the price per share and the dividends. So people tend to talk so
much about the capital gains. The movement of the market,
they forget about dividends. Some people don't even know
there are [LAUGH] dividends. That's actually the whole reason for
being for the stock market. Ideally anyway,
you buy shares to get dividends. And, in fact, if you look at history,
up until recent times, most of the returns you get on
the stock market are in the dividends. People think, well no,
isn't it just that the market has soared? Well, historically, over 100 years,
dividends are more important. The stock market goes up and
down, creates capital gains and capital losses, but
dividends are what it's all about. So companies don't have to pay a dividend
but typically young companies don't. Once they're mature they like
to start paying dividends and it signals to the world that
they're really making money. If you're investing a company
that never pays the dividend, you start to wonder,
is this real or is this a fraud? I never get a penny from them. So once they're into making money, they think it impresses investors
to get dividend checks. All right, I remember my own company. We incorporated in Delaware. My first company,
Case-Shiller Weiss Incorporated. And we didn't have to pay a dividend. I remember we had a board meeting
where we talked about exactly this. We've never paid a dividend. We gave shares to a lot of
our employees as incentive. But someone said,
they don't even believe in it. Nothing has ever happened. So we should pay a dividend. But we didn't. We held on. The employers eventually did
well when we sold the company. They found out that their shares
really were worth something. But we should have started paying
dividends and make it clearer. We didn't.
So when a company pays a dividend,
what happens to the share price? Well, very simple, it drops because
the company used to have the money and now it doesn't. It paid it out. The share price pretty much has to drop
and I don't suppose it always does. Because funny things happen but the basic idea is that a share drops
in value when a dividend is paid. But I have to qualify that. It doesn't drop in value when you get
the check in the mail for you dividend. That would be variable anyway, right? They don't necessarily pay
them out in the exact moment. So a company has to define what
they call an X dividend date. That means, they will pay out
the dividend, this dividend, typically chorally dividend
every three months. They'll pay out this dividend to
shareholders of record on this date. So company values drop routinely
on the ex dividend date. That doesn't mean bad news
about the company at all.
So I had a question about companies and
different dividend payment systems. So some companies like to boast
about they always pay dividends. They never miss it. Why would they want to emphasize this? And what would happen if they had
to cut back on their dividends or they don't miss their
dividends in a period? >> Well, I think this is an essentially
behavioral human question. So the reason they don't want to
miss a dividend is because they think that will harm
the investor support. They don't want to see
their stock price fall. If the investors lose confidence in
the company, these tag price can fall and then the management starts to
worry that that'll be taken over. If the price gets too low, take over, people will think, I'll buy it and
I will shut it down and they'll sell it of all their assets may
be you can get, if it gets low enough. So it's a big fear they don't want
investors to have a bad attitude. So then why would you as an investor
be disturbed if a company didn't pay a dividend? Well, I think it's a sort of
fundamental human miss trust. You don't know that these guys are on
the level, maybe they're crooks or maybe they're not. It's like missing a payment
on your credit card. You have a credit rating that
depends on you actually making these monthly payments. And you could take the attitude, well,
I'll miss it once and I'll pay the fine. What difference does it make? But your credit rating will
go down if you do that. So most people personally think,
I'm going to pay every month, this is something I'm really going to do. And they kind of imagine that it's
like that with dividends with company, if they miss a dividend it means they're
kind of unreliable, untrustworthy, now they didn't have to think that but that
apparently is how a lot of people think. So that's why lots of companies don't
ever want to miss paying a dividend. >> Couldn't missing a dividend also be
a real indication of financial trouble though and maybe that's why investors-
Right, right. >> Why a red flag is raised? >> Yeah, now the thing is that
a dividend is not promised. The corporate law says that they can pay a dividend at the discretion of
the board whether they want to or not. And many companies go years
without paying dividends, but the public might have some preconceived
notions and think it's like my credit card bill and if their not paying,
there's something wrong here. Now they could stop paying a dividend for
perfectly good reasons. Like they want to do something
with it that's more productive, but the investors might not understand. By the way, I don't mean that firms never
miss paying a dividend, I'm just saying that some firms pride themselves
on never having missed a dividend.
Common vs. Preferred

I've already suggested, but I didn't really state it clearly, the difference between common and preferred stock. We've been talking about common stock. Now common doesn't mean plain and not pretty, it means held in common. The word equity refers to common stock as well. I'll come back to that. What's the difference? Preferred stock has a specified dividend which does not grow through time. And like common stock, it doesn't have to be paid. Now again, there might be slight differences in state law. We have 50 different states in the United States and other countries have similar institutes, it's a complicated law. But, typically the deal is this: the company is supposed to pay out a fixed dividend to the preferred stockholders, but it doesn't have to. But, it cannot pay a common stock dividend until it's paid up on its preferred stock dividends. So if they don't pay them, then they have to- if they haven't paid their preferred dividend they've got to make it up eventually.
But in contrast, corporate bonds have a contractual obligation to pay a dividend. So that is, that if the company gets in trouble and it doesn't- as I say dividend, a coupon, on the bond. If a company gets in trouble and doesn't pay out its coupon the shareholders can come back and sue, force the company into bankruptcy. Preferred stockholders can't do that otherwise they're kind of like corporate bonds. During the financial crisis 2000, 2008, 2009, the U.S. government got a lot of preferred shares in companies for bailing them out. The U.S. government didn't want to get common shares, it wanted to get paid back. It didn't want to push them into bankruptcy by creating a new form of debt. So the U.S. government got preferred stock in the company. Why didn't they get common stock? Hey, this is America. The U.S. government, if it were to be buying common stock this would be socialism. The government would be owning parts of companies and they didn't want to do that. So they bought preferred stock. So for example the U.S. government and the Canadian government I think had a lot of preferred shares in General Motors.
Corporate Charter

Now, the basic corporate
charter emphasizes that all common shareholders
are treated equally. They don't have to pay out dividends to
them, but if they do pay out dividends, it has to be every share gets the same. And that's where the word equity comes in,
it's equality of shareholders. Does not have to pay dividends,
it doesn't ever have to pay dividends. But you trust that the Board will
pay dividends, because the other shareholders want the money, they can't
get at it without paying you too. The firm can also repurchase shares
instead of paying a dividend. No law saying that they have to,
they can both issue new shares and they can repurchase shares,
the Board decides. There's also other kinds
of corporate liability, warrants which are a form of option,
convertible debt. They can do whatever they want, but the fundamental thing that
ties it down is that all shareholders have one vote,
and they elect the Board. Now there are critics of
shareholder democracy.

Notice notably Berle and Means wrote
a book in 1933, that was very influential. Arguing that while you've
described a system of corporate governance
that sounds plausible, and probably does work for little companies,
but it might not work for big companies. Well I know when I set up my own
little company, Case Shiller Weiss, there were three of us, and
well we had one more major shareholder. We got together, and
it was very clear that we voted and things happened because we were involved. So the democracy, it just seemed
perfectly natural and functional. But Berle and Means thought that it
doesn't work so well for big companies. The same reason may be why voting, when there are millions of people voting,
doesn't work so well. So I know what you think whether,
do you vote? Okay, as you go to the voting booth in an
election, does it ever occur to you that my vote doesn't matter unless the rest
of the people are equally tied, right? If exactly half vote for one candidate and
exactly half vote for the other candidate that it's tied and my vote would decide,
otherwise my vote doesn't do anything. So what's the probability that
my vote is the deciding vote? Well if there's millions of people,
the probability must be miniscule, so if you were really rational,
you wouldn't vote. But people still vote in elections, and
this must be out of some sort of patriotic feeling or a sense of obligation.

But when it comes to corporations,
those senses aren't so, you don't feel patriotic for
a corporation. So and a corporation has an election,
why do I even bother. We're holding diversified portfolios,
aren't we? So, I've got a hundred different stocks, I can't keep up with how
they're all being managed. [INAUDIBLE] during election and
vote my share. I'm only a tiny, tiny fraction,
so why should I do that? So Berle and Means said that, while in practice we have
shareholder democracy, in practice the democracy is imperfect. It's really self-perpetuating
Boards of Directors. So their book was extremely
important historically. And what it led to is new regulation that
tried to allow for takeovers of companies. What Berle and Means said, is there's
a lot of companies were ill managed and managed for the interest of the board
of directors because they just owned, effectively owned, they can't pay
themselves big amounts of money. They can pay fairly generous salaries,
they can hire their friends and give them nice jobs as sort of
ripping off the company. The shareholders, some of them might
hear about this and get upset but it's hopeless. You can't influence the votes of so
many people.
So they made it easier, 1935
the Securities and Exchange Commission under authority of the act that
had just created it in 1934, established rules for proxy contests. So that people who wanted to change
the governance of the company could reach the shareholders and ask them to sign
a contract to let you vote on my behalf. You would give them
the right to be a proxy for you at the shareholder's meeting. And they made it,
companies didn't want to help outsiders reach their shareholders, they
wouldn't publish the list of shareholders. So there was no way that if proxy contest
could have been done prior to 1935. But now they made it because
they began to think, we have to make sure
holding democracy works. This is the Roosevelt era,
which was very left wing. But the really wonderful
thing about the Roosevelt new deal was that it wasn't socialist. It was maybe motivated by social
harmony and concern about poor people. But it left intact the corporation. So this doesn't sound like
Franklin Delano Roosevelt at all. But it is, it's trying to make Democracy work and
they wanted shareholder democracy to work. So there have to be election contests in
corporations like we see in politics. In 1956,
amendments made proxy contests difficult. But then people later as we move
to a more free market governance, relaxed the 1956 amendment so
that proxy contests came back.

Now some companies have classes of shares,
as permitted by state law. So you can have both voting and
non-voting shares. Berkshire Hathaway, which is
the company of Warren Buffett, who has both class A shares that have voting
rights, and class B shares do not. I have to update this. What the Class A shares self or not,
it was recently 200,000 a share. That doesn't mean, this is a big company. It only means they don't split. And it would be 30 a share if they
split like other companies, and it wouldn't make the company any less
valuable, maybe I'm over stressing that. The New York Times has both
Class A shares and Class B. Class A has less voting
rights than Class B. Which allows the descendent of
the original Adolph Ochs family still to control the company. Why do they do that? Well, they think that the New York Times
serves a higher purpose. That is, it's not out for profits, it has some profits but not entirely. So they gave the original
New York Times family more voting rights than
the other shareholders. This has been under criticism recently but
still is maintained. Facebook, Mark Zuckerberg recently, I don't know what the percent is right
now, but had 28% of its shares, but 57% of its voting shares, which
basically Mark does whatever he wants. If he has the majority of votes in the,
but that's because of the classes of shares.
Corporations Raise Money

So, now, how do companies raise money? You're in a company and
you're trying to make a profit. You need money, say to build a new
factory, or to launch a new ad campaign. So, you need the money now and
you get profits later. How do you get the money? Well, there's two major resources,
ways to do it. Well, I should, maybe three. One of them is retained earnings. I'll list that first. You can wait until you've made
enough money, you save it up, and then you can build your new factory. That's one way. But it's slow because you have to wait
until you've got the retained earning to do that. Often, young companies don't
have much earnings because they're putting everything
into the future. Another thing you can do is borrow money,
either through banks. You can go to a bank and
say I'd like a loan for my company. Or you can issue debt and
sell that through a broker. You will issue a corporate bond,
which brings in money. And you can issue shares, new shares. So suppose there are a million
shares outstanding. You can issue another million shares. Now, the shareholders of the company,
when you do that, are going to look at that and
say wait a minute. What are we doing here? I used to own 10% of the company,
and now I own only 5%, so I'm not so sure I'm happy about that. But then you on the board would say, but
don't worry, we brought in millions of dollars for, and you own a share of
that so the company has more now. So it's not bad for you, we need
the money because we need to invest. And I think people understand that.
So this is called dilution. When they issue more shares,
your share in the company goes down, defined as the total of shares
you have divided by total shares. And so, do you feel happy, or not? Well, you have to understand
that it's diluted you. You no longer have the same
vote that you used to have. You've given up some voting power in
order to get money to expand the company. You might come to a shareholder or
a shareholders' meeting and complain. But they'll say, but
look this is the way it works. We can't expand without money. And this will make you, you'll' be treated equally to these other
guys that came in and bought new shares. So you might as well back down. I guess that's the way,
all these big companies did that. So that if you're an initial
shareholder you once owned a big fraction of the company. It keeps going down but
the company keeps going up in value. But here's why they call it equity,
because all common shareholders are equal. Now, so
what about issuing shares to get money? Well, some people said that issuing
shares isn't very important anymore. That companies, when they need money, they borrow money or
they use retained earnings. Karl Marx thought that. He said all this trade in stocks
is trading mostly existing shares. It doesn't bring money into the company. All this transaction, it's just gambling,
that's what Marx said. All these people playing a game. It's only when the company issues shares
that share price matters economically. And Marx thought they
don't do that very much.

Stewart Myers, who's a professor of
finance at MIT, wrote an article in 1984, arguing that well, I don't think he
put it this way, Marx was right. I'm sure he didn't say Marx was right,
but he was effectively saying that. because he looked at the data and he said,
firms don't issue, when they first start, they issue a lot of shares. But after that,
they're not issuing very much. So he said, proposed what he called the
Pecking Order Theory of corporate finance. How do a corporation,
this sounds like behavioral economist, now he might shudder if I identify
him as a behavioral economist, but this is what this sounds like to me. The best way to raise money for
corporate actions, according to what he said boards think,
is retained earnings. You feel most comfortable. You go to a board meeting and say we
need to build a new factory and, but, we've been making a lot of money, and
we've got all this cash lying around. We'll use the retained earnings
to build a new company. That feels really good
going into the board. They'll say, well, why not? They'll go for that. But then if you say let's go
to the bank and borrow money, then they get a little nervous
because bankers sometimes ask for the money back and
then you can be in trouble. So they're not quite so willing, so
that's lower on the pecking order. But then the other thing you can say,
all right, let's issue a new share. Now, they get really creepy. Now, they're thinking,
are my votes going down? I don't like, it's so
often shareholders are on the board. They're thinking, now, I"m going to
be giving up power to other people, and if our profits don't go up, then we're going to be dividing
them up among more people. So they don't like that. So Stewart Myers' article was very
influential because it sounded right. This sounds like the way I can imagine
myself behaving as a board member and he showed statistics emphasizing that.

Now as of 1984, most firms had not done a single equity offering
in the last 20 years. And when asked,
are you thinking of issuing new shares, did not even contemplate doing it. From the years 1973 to 1982, 62% of capital expenditures
came from retained earning. That is what companies
were doing at that time. And only 6% from issuance of new shares. So if they never issue new shares, then what difference does the share price
mean anyway to corporate activities? So this was a Marx was right conclusion.

But they were criticized,
notably Eugene Fama and Ken French. This is the Eugene Fama that we keep
talking about, the efficient markets guy, but I think they were right here. Stewart Myers choice of
1973 to '82 was atypical. The stock market crashed in 1973,
and it was still low, so you didn't get much money for
the new shares you issued. Of course,
nobody issued new shares, and, but even so, there was some forms of
equity issuance even in that period. For example, they issued corporate
shares to employees as compensation, or they had Warrants on the stock
that were given to employees. So there was some issuance, even then, but the amount of equity issuance
increased right after. They gave, 86% of firms issued some equity between 1993 and 2002. So it's really not true. Marx wasn't really right
about the price of a share in the public market matters for the
amount of money that a company can raise. So if the market price goes up, the company can get more
money by issuing shares. And that encourages them to do that and
make more investments. When the stock market goes down,
the company starts looking at it. Typically, the board members are still
optimistic about the company. And you say let's,
we're down to $3 a share. You might be talking about doing
a reverse split to try to bring it up. But you're thinking,
are we selling these shares for only 3? I had my life's dreams. We're going to diluted down for just 3? I don't believe that and wouldn't do that.
Dilution

Sometimes companies will
issue a dividend in shares, and it's called a stock dividend. So you might get a letter from your
broker saying, congratulations. The company has now paid
a stock dividend of 5%. So you had 100 shares,
you now have 105 shares. And the price per share is 30, so you've got five new shares. It's like getting a dividend of 150. But that's what most people think. What is the next question
you ask your broker? Let me get this straight. The company has issued new shares, so
that I can be paid a dividend in shares. And I now have 105 shares, is that the same as getting $150 in cash? Now think about it. The question you would ask your broker,
do you see where I'm going with this? The question you would ask your broker is,
wait a minute, every share holder is getting
these share dividends, it's equity, they can't pay me a stock
dividend without paying the other. So the total number of
shares went up by 5%. So I'm calculating what fraction of
the company I own, it's the same! So then you would go to the company and
say, what is this nonsense? You're paying a dividend and shares,
I figured out that means nothing. The company would be kind of
embarrassed if you asked that question. They would say, what would they say? They might say if you could get them
on the phone, say yes you are diluted, you did get shares and
you were diluted down by the same amount. But we think this price per share will
hold, and it's going to be good for you. They'll just try to talk
their way out of it. Typically they issue stock dividends
as just, it's kind of a trick. This is fishing for fools, [LAUGH] but
they could be well motivated in doing it. They have to keep your morale up. Maybe they weren't going to pay a cash
dividend, so let's do a stock dividend. Let's make a public statement that
the company's doing really well. And if anyone brings up dilution you say, but no, we're doing so well. We wouldn't issue a stock dividend if we
thought that it would make the price per share fall. So a few of us might say,
okay, I can do that. Now there was a time once when
the Internal Revenue Service proposed taxing stock dividends. Well, why not? You just got a dividend and
you should declare it on your taxes. So some companies running to the IRS, and now they explained it with perfect
clarity to the tax collector. No, no, no you've got to understand. This isn't really a dividend. This is just a paper or something. You can't possibly tax them on this,
because they didn't get anything. So the IRS backed down and
it doesn't tax stock dividends.
You just talk briefly to how
some firms never pay dividends or to go many years without paying them. Why do these firms think
it's optimal to do so when these other firms boast
about always paying dividends? >> Well typically the firms that never pay a dividend are young firms in
a rapidly growing business, where they tell investor,
it's a different kind of investor. The one that by stocks that have
never missed pending a dividend, that's grandma, okay? [LAUGH] And grandpa. They have old fashion ideas, but young people are more likely to buy
stock that doesn't pay a dividend. It's also especially popular
in the last 20 or 30 years. That's a long time for you, I know. [LAUGH] When the Internet started
loading up steam in the 1990's. They were setting up companies like
Amazon and was it Google, I'm not sure about the years, but around that time
a lot of young companies were set up. And people said, this is an opportunity. Right now,
there's this revolution in the Internet. You've gotta jump on it, because
it's going to go to the first mover. And to a significant sense, that's true. So the kind of people who would invest in
some startup Internet company back then. So we'd say don't pay me a dividend, I want you to move otherwise
you'll be a loser. So in fact it almost became reversed that companies prided themselves
on never paying a dividend. It used to be that
the New York Stock Exchange wouldn't list a company
that never paid a dividend. And it was prestigious to be listed
on the New York Stock Exchange, but there is this other young
exchange called NASDAQ that would list you whether you've paid a dividend or
not. So Microsoft went on NASDAQ not
on the New York Stock Exchange. Then years later,
when Microsoft became big and important. The New York Stock Exchange said,
in its dignity, said, we have now decided that Microsoft is okay for
listing on the New York Stock Exchange. But you know what Bill Gates did? He said, no way. I don't care about your prestige. [LAUGH] NASDAQ is better,
because it's the go for it companies. So you're right,
there's different subcultures. Some which appreciate a dividend, and some
which think it's the sign that you're old school, but you know firms have clientele. Investors that invest in their firm. And so you appeal to your clientele,
the old utility companies are never going to get the young hot
shot investors anyway. [LAUGH]
Share Repurchase

Now, share repurchase is
another thing that happens. That instead of issuing
new shares to raise money, the company can repurchase
shares outstanding. Go out on the market like you, and
the company buys back its own shares. That's the reverse of delusion because
the number of shares goes down. And if you didn't tender your shares,
if you didn't pay, if you didn't sell your shares at
the time of the share repurchase, you own the same number of shares. That means that your share
repurchase pushes up the amount that you own of the company. So share repurchase in a sense
is like paying a dividend. It's an alternative way
of paying a dividend. So let's think of it hypothetically. Imagine that the company is
about to pay its dividend. It's been paying $2 a quarter regularly
per share and they're about to pay it. And then someone says, why don't we
send out a different letter this time? Instead of saying this is a dividend,
let's send a letter that says this $2 is
repurchasing 1% of your shares. Of course, everyone gets the same letter. So if you get this in the mail,
you would say what's this? I got my $2 dividend check and I also get
a letter saying this is share repurchase. Now, you might be confused,
what does this mean? Well, I tell you one thing it means, it's not taxed because well
not taxed the same but forget about taxes for the minute. What does it mean whether I get a letter
saying this is a share repurchase or this is a dividend? It's $2, and the share repurchase
if it's everyone equal doesn't affect the fraction of the company
that I own, so the letter is nonsense. It's just the same thing
as paying a dividend.

So they do a lot of share repurchases,
especially recently. It's been a big thing in America
since the financial crisis. Now, some people say that's because
the stock market was during the financial crisis. The stock market was low, and so
companies were buying back their shares at a low price, that's what was said. But now prices are way back up again and companies are still
repurchasing their shares. So what's going on here? There's a lot of share repurchases lately. Why do they do this? It's been 2% of shares per year, which is comparable to the dividend rate,
the rate of dividend. On the aggregate US stock market
has been something like 2%. So how do they get that? Well the important thing is, it would seem the important
thing is there's a tax break. If they do share repurchase
instead of dividends, it's the same thing and technically,
but you can fool the IRS. Suppose the company pays
out a 2 dividend, and then I would get 2 in dividends, and then
I would have to pay income taxes on those. It used to be you had to pay
them at your marginal tax rate. Now it's 15%, or
it's capped at 15% of the dividends paid. But if they do share repurchase,
now if I would still have $2 more. If I didn't participate in
selling my shares to the company, then my value of my shares
goes up by something like $2. But I don't have to pay taxes on it
because I don't have to pay taxes until I sell. So I can postpone them maybe indefinitely. Maybe I'll never pay taxes on them. So I like that, I like share repurchases. Now incidentally right now in the United
States, the capital gains tax for small capital gains is capped at 15% also,
but for higher amounts it's 20%. The real thing though that's different
is that capital gains taxes, that's for long term capital gains. Capital gains taxes do not have to
be paid until you sell the shares. So it allows you to postpone,
maybe for the rest of your life, the tax on the amount paid up. So there's a tax incentive for
share repurchase rather than dividends. I think that is a substantial
part of the reason why companies are relying
more on share repurchase. Those other issues though, these are behavioral finance, one thing
is that people just don't get it. Most people have not taken
financial markets and they don't understand what's going on. So, if you were to say,
we're not paying dividends any more and we're going to do share
repurchase instead.
First of all, you get the IRS,
if you do it every quarter, if you do a share repurchase every quarter
and you make this big announcement, the IRS will then say, maybe this is
a dividend even though you're calling it. You've got to be devious about it. You can't do it every quarter. But suppose you did that, the people would
react immediately to the loss of dividend. I'm talking about grandma and
grandpa who are retired and don't know anything about finance. That they got a letter saying
we're canceling your dividend. They would panic. They'd say, well we have a rule that we
only live off of interest and dividends. They would be upset. And some companies boast that they
have always pay the dividend of, this is very effective for grandma and
grandpa who often have a rule that I never dipped into the principle,
I only live off income. And I need that to buy food every quarter,
so I need those dividends. I mean you could tell them no you don't, you can sell your shares any time you
need to sell some of your shares. And they're going up in value because of
the repurchase, but they won't get it. There's also other thing about
a price pop after repurchase that might encourage share repurchase.
PDV of Expected Dividends

What does the stock market value? Now as I said last time, a lot of
people think the stock market, you buy into the stock market so that it goes
up and you can sell at a higher price. But was is it? What are you pricing? Well, some people have
never thought about that, they just want to know whether it goes up. So what I was saying last period,
I'll repeat it, that most of the return people
have gotten historically from stocks is in dividends,
not in capital gains. And in fact,
it's correct to think that efficient markets implies that what
you're really pricing in the stock market is
a claim on dividend.
Suppose a company were to say we
will never pay a dividend again. Now we're going to put it into our charter
that we will never pay a dividend. All of our profits go to charity,
let's say. Well, you can do that, but
what's the value of a share? There are no shares, if there were,
they'd be meaningless, so they'd be worth nothing. So it's all about dividends,
there's two important ratios.
There's the price earnings ratio, price
per share divided by earnings per share. And there's the price dividend ratio,
typically dividend price ratio, where it's dividends per share
divided by price per share. Now let's simplify things and
not worry about that distinction. Suppose a company is paying out
all of it's earning as dividends, then the two are the same. So let's just talk about
the price earnings ratio. What does that mean? It's different for different companies,
some have a high price earnings ratio. It could be as high as 100,
that's very unusual. Which would mean that you'd have to wait
100 years to get your money back based on dividends, if you bought it. That's a long time to wait, more typically the price earnings
ratio is something like 15. So you'd buy a share and
in 15 years, if you're getting all the earnings as dividends,
you'd have your money back. So the price earnings ratio should be
something like that, like 15 right? 10, 15, 20, not 100, you wouldn't buy into an investment
that takes 100 years to pay out.
So what determines
the price earnings ratio? Well, I refer to the idea that efficient
markets idea is that the price of a share is the present discounted value
of its expected future dividends. And then I can apply the Gordon Rule,
which I mentioned recently, which says the price should be equal
to earnings divided by r minus g. Where r is the interest rate or
discount rate, and g is the growth rate of earnings, so the
price earnings ratio is 1 over r minus g. Now this is a very important model,
because it gives you a theory it's an efficient markets theory,
why some firms have high price earnings ratio and others
firms have low price earnings ratio.
It always has to do with r and g, those are the only thing
that goes into this formula. So if a company has a low
price earnings ratio, according to efficient markets,
according to this, I should say efficient markets
is not precisely defined. There are many different
efficient markets models, but I'm taking this sort of basic
canonical present value model of efficient markets. And it would say if a company has low PE, that means either r is high for
that company, or g is low for that company,
or a combination of both. Now why would r be high for a company? Well if you believe the standard
theory which has been taught for 50 years in finance courses, we have
the security markets line remember? The expected return on a stock is a function of it's
covariance with the market. So that would mean that companies
whose return covaries with the market should tend to have via this r thing,
should have low price earnings ratios. In simple terms, they're riskier
in the correct sense that provide. They're riskier in that they
co-vary with the market.
The other thing though is g. Some companies have very
high growth prospects. That everyone knows, they have some
patent say, or some good technology. Nobody can compete with them,
they're just starting out. Of course you expect
their earnings to grow. But in efficient markets,
that's not a reason to invest in them. Because the price will reflect
the growth in earnings already, so it will already be discounted
into the present value. So anyway, high growth companies should tend to have high PE,
a low PE would be a low growth company.
There are often good reasons for
a low price earnings ratio. One is that the business is very risky and
so people don't want to put
a lot of money into it. And another one is that the business might
have a poor earnings growth outlook. That earnings is likely to fall,
the classic example of that is rail roads. That was the in thing in the 19th century, by the early 20th century it was
looking a little bit old fashion. And we've gone another 100 years, so they're really not the most
rapidly growing investment. So they get beaten down,
the price gets beaten down. But you know what? Railroads are here to stay, and there's always a price that
makes them a good investment. So when were railroads a good investment? Well, I was thinking around 2000,
when the market was at a peak. Well I call them Millennium Peak. And it was all this
Internet dot com stuff. You shouldn't have been
buying dot com then, usually. You should have been buying
railroads because they were just forgotten at the time.
The question is, does it work? Does the efficient markets model work? Well, I've been always saying that
efficient markets is a half-truth, and it sort of half works. Especially with as I say,
railroads are not high PE stocks. But there's another
approach to investing which goes back many years called
value investing, okay. Notably Benjamin Graham and David Dodd who were teaching
finance at Columbia University in the 1930s they wrote a textbook
called Securities Analysis. And in that textbook they outlined
their thought that PE varies for other reasons than just this technical
reason that we talked about, because companies go in and
out of fashion. And when they're hot,
people bid them up too high. And then when they're ignored, they just
ignore them and forget about them, and they get low PEs. So value investing, as outlined in 1934
by Graham and Dodd, is still with us. And it still works, although it
hasn't worked in the last five years. It comes and goes., but
generally it has worked.
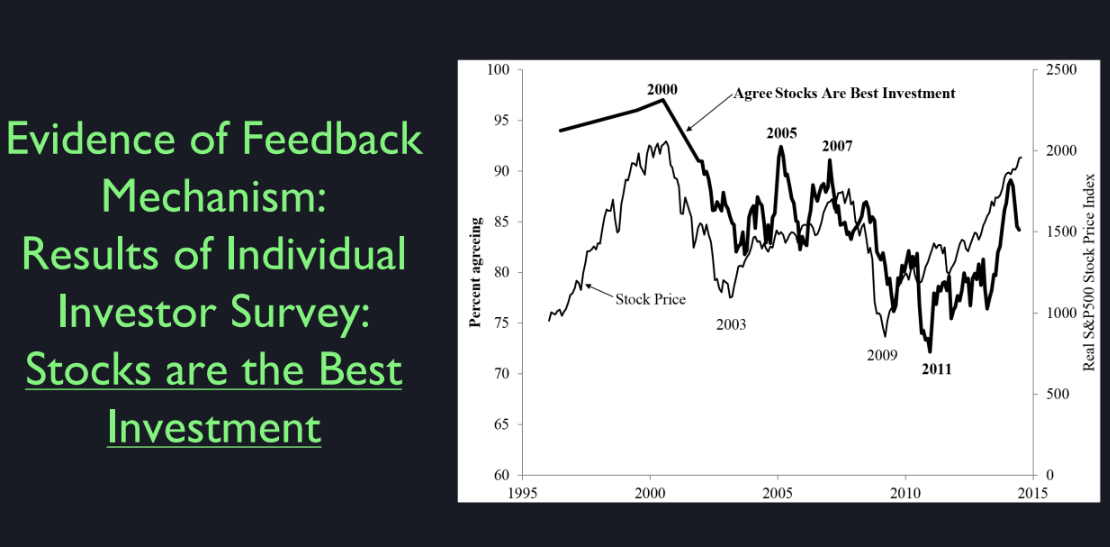
This is going to apply also to real
estate, but let me just move on to. This is a figure from the third
edition irrational exuberance that you have and
it gave some sense of value investing. The thin black line is the stock price, it is the S&P 500 index corrected for
inflation back to 1996. And the solid black
line is a tabulation of a questionnaire item I've
been doing since 1996. So I started doing surveys,. Actually, I started in the 1980s
doing surveys of investors. These are individual investors,
high income. I mean, income $200,000. I figure those are more
representative of the stock market. I like low income people, but I don't survey them when
asking about the stock market.
So the question was do you agree
with the following statement? Stocks are the best investment for
long-term holders who can buy and hold through the ups and
downs of the market. I'd heard that phrase said so
many times in 1996 that I thought, I better start tabulating. Do people believe that? Now, this theory is not
what we say in this course. This course emphasizes diversification and not looking for the best investment, but
I just want to know what people think. To my amazement,
almost everybody thought that's right, stocks are the best investment. So you can see, in the year 2000
which I have marked up here, the something like 95% of these people
thought stocks were the best investment. Now there could be a little of a bias. These are people who agreed
to fill out my questionnaire. They must have found it interesting,
so it may not be completely accurate. But it's certainly
an awfully high proportion. I almost don't believe results like this. It was really into the culture that
smart people invest in the stock market. But you notice the stock market had
been rising for years prior to that. And this is the peak of what I call
in the book, the Millennium Bubble, this is the new millennium. And then we celebrated the new millennium. It was great, do you remember it? Probably not very well. And look what the stock
market did right after it. And then look what happened
to opinions about stocks are the best investment right after it. It came down with it. The stock market bottomed out. So did their agreement with that. Now it's not a perfect fit,
but I see a strong parallel. This inclines me to value investing. This question didn't ask about, do you think the stock market will go
up next year or the next two years. It's about stocks are the best investment. It's like timeless. So why should opinions about something so
timeless be so variable through time? And why are they so influenced by
the recent behavior of the market? But I think that's human psychology and
behavioral economics.
Why do firms pay dividends?

Now, this comes back to the funny question that we discussed previously last period. Almost all the value of the star Inherently is due to the dividends. But firms don't even have to pay dividends, and they often go through years and years without paying dividends. The other thing is, and we have to be clear about this, firms can get money to their shareholders in another way besides paying dividends. You can buy back shares, and firms do that. It's the same thing, and we talked about that, right? You could send a letter with your dividend check and say, "Well, we're really buying back shares." And it wouldn't make any difference, except to the IRS who might decide something different about taxation.
But there are other reasons why firms pay dividends. Hersh Shefrin and Meir Statman described what they call a self-control theory of dividend. Now, this sounds funny, but there's a lot of people who invest in stocks and have a personal rule of thumb that I will never dip into principal. The model investor in the stock market in the United States is a 80-year-old woman. I'm exaggerating, not quite 80 years old, a widow. And sometimes they are following the instructions of their late husband, who said never dip into principal, that's for the grandchildren and they never touch it. But then if dividends go to zero, she's in trouble, she doesn't have any income. This sounds really silly, but it actually applies even to such institutions as Yale University, who a half century to a century ago, I think was influenced by the same thinking.

So we won dividend paying stocks, and we didn't want to touch the principal. That all changed when we got David Swensen to take over and became a more sophisticated investment manager. Another theory why firms and some of the influences are thinking about dividend, by Bhattacharya, Hakansson and Ross, is that they use dividends to prove to the public that they're really worth something. It's called a signaling theory is a theory that you do something not for its intrinsic value but because it proves something about you. So Michael Spence, who used to be dean at Harvard College surprisingly wrote a famous article saying, college educations are largely signaling. This sounds awfully cynical from the Dean, but he did say that. Why do you go to college? You want to prove two things, you're smart, and you're not mentally ill. Alright, and you can actually slog through all this nonsense that you get in college and you make it up four years later. And so I think there's some truth to this. I hope that's not the only reason you go to college. Why go through all four? Why don't you do a Bill Gates and drop out? You already proved that you could get into Harvard. Why don't you just drop out? Well, you might, if you're an entrepreneur, just drop out because you don't have to prove anything to anyone, but you want to stay the whole four years because that separates you from the people who are unstable, who can't hack the work. So you're proving your work ethic. Well, I'm not saying that's right, that's a signaling theory.
Well, it's the same idea that the Bhattacharya, Hakansson and Ross had that firms are signaling. Life is filled with signaling. You're trying to prove one thing or another by doing something. And so firms pay dividends just to show there's real money here. We've really got it. And if we were on the verge of bankruptcy, we wouldn't do this obviously because we would be risking going under. So it's a proof that we're there. We've made it. And I'm sure there is some truth to that. But this kind of signaling does impose taxes. Remember dividends are subject to immediate income taxes, whereas repurchase of shares will not involve any tax until you sell the thing again, sell the shares again.

John Lintner was a professor at Harvard Business School, who said that he interviewed a lot of firms about dividends and how they decide. This is unusual for any efficient markets era when he was writing. Usually, he never interview anyone just trust to markets, and so no one can tell you why they do things. But he interviewed three people who set dividend policy for firms and asked them how they did it. And he found that they said all sorts of things. But he said, and the bottom line is, they just gradually adjust dividends toward earnings per share. So they have some target payout ratio. I was assuming above it was one. They were paying out all their earnings, but, in fact, it's less than one typically. And so they change the dividends only slightly each quarter, reflecting an adjustment towards the target dividend price ratio.
So you can see that that tau, the target ratio times EPS is the dividends they would have with today's earnings per share. And if it's above their previous dividends, are raised dividends but not enough to put it there. That's because earnings jump around, and the other thing they told Lintner, "We don't like to cut dividends. We never want to cut them. That's embarrassing. People start calling us up and said, "The last quarter you sent me a check for this and this. I need the money. Why are you cutting it?"" And you'd have to tell some story. "Well, our earnings weren't as good as we thought." You don't want to tell a story like that. So when earnings jump up, you don't raise your dividends right away. You just lag behind. And that's what the Lintner model says.

Just to give you some idea though, that back in 1968, general public utilities court, which was a utilities company, proposed a substitute stock dividends for cash dividends, and offered to sell the stock dividend to the stockholders for a minimal cost. And we wrote a letter to the shareholders saying this would save them $4 billion a year in taxes. He's saying, "Instead of paying the dividends, we decided to buy back some of your shares. So you now have less shares, but you get the same check, and you're going to get the same check in the future because everybody's shares went down. He explained all this, and they didn't get it. He was just trying to save them on taxes. But you know what happened? He got death threats.
Investors are emotional, and somehow, they didn't like the sound of this. It sounded immoral. Cashing in on principle, you're selling our shares. We don't want to sell our share. We just want the money. And it just lost it. People don't think about taxes, even high income people who might own shares, which goes to show why I don't really believe in efficient markets. It's somewhat true, but there's a lot of people out there who don't think very much about investing. And it's such a complicated thing to imagine that the market gets it right. Now, on the other hand, efficient market is still valuable because there is still a lot of smart money. They just don't completely dominate. There is a lot of smart money that will take advantage of mispricing. But they do it at some risk, and it's not a sure thing. And so they hold back a little bit and there are mispricings all over.
Lesson #9 Quiz



Module 3 Honors Quiz
Question 2
To calculate the amount of money you will have at the end of the year if the interest is compounded continuously, we can use the formula for continuous compounding:
A = P ⋅ e r t A=P \cdot e^{rt} A=P⋅ert
where:
- A is the amount of money accumulated after time ttt
- P is the principal amount (initial investment)
- r is the annual interest rate (expressed as a decimal)
- t is the time the money is invested for in years
- e is the base of the natural logarithm (approximately equal to 2.71828)
Given:
- P=1000
- r=0.20 (20%)
- t=1 year

Question 3
To calculate the current yield to maturity of a consol (perpetual bond), we use the formula for the current yield, which is given by:
Current Yield = Annual Coupon Payment Current Price \text{Current Yield} = \frac{\text{Annual Coupon Payment}}{\text{Current Price}} Current Yield=Current PriceAnnual Coupon Payment
Given:
- Annual coupon payment = 6 pounds
- Current price = 150 pounds
Substitute these values into the formula:
Current Yield = 6 150 \text{Current Yield} = \frac{6}{150} Current Yield=1506
Calculate the current yield:
Current Yield = 0.04 \text{Current Yield} = 0.04 Current Yield=0.04
Convert the decimal to a percentage:
Current Yield = 4 % \text{Current Yield} = 4\% Current Yield=4%
Therefore, the current yield to maturity of the consol is:
4 % \boxed{4\%} 4%
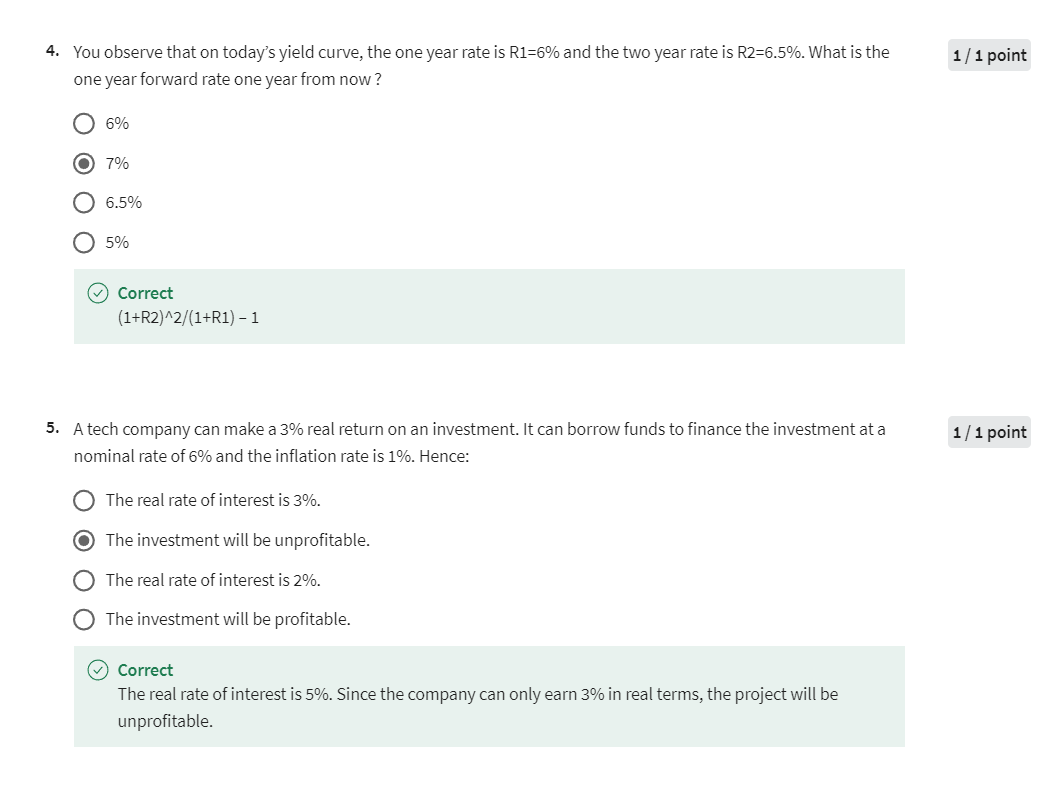

Question 6
If expected inflation is less than actual inflation, then wealth will be redistributed from lenders to borrowers.
Here's why: When lenders and borrowers agree on a nominal interest rate, they usually factor in the expected inflation rate. If actual inflation turns out to be higher than expected, the real interest rate (nominal interest rate minus actual inflation) that borrowers pay is lower than anticipated. This means that borrowers end up repaying their loans with money that is worth less than expected, effectively reducing the real value of the debt. Consequently, lenders receive less real value than they had planned.
Thus, the correct answer is:
Lenders to borrowers.


12题的正确答案是Stock repurchases are more tax advantageous than are cash dividends.
解释如下:
The statement "A stock repurchase increases the market value per share" can be true in certain contexts. However, it is not universally correct in all cases, as it depends on various factors such as market perception, the company's financial health, and the reason for the repurchase.
While stock repurchases can increase earnings per share (EPS) by reducing the number of shares outstanding, thereby potentially boosting the stock price, this outcome is not guaranteed. Therefore, the statement "Stock repurchases are more tax advantageous than are cash dividends" is generally more consistently true across different scenarios.
Question 13

A dividend yield which is smaller than that of an average traded firm within the market.
高于市场的市盈率(P/E)通常意味着投资者对公司的未来收益增长有更高的期望。因此,这些公司通常会有较低的股息收益率,因为它们可能会将更多的利润再投资以促进增长,而不是支付高股息。
后记
2024年6月29日15点04分完成week3的学习。从2024年6月17日开始学习week3,总共历经12天,花费在金融市场估计是三四天的时间。
无论如何,这门课要有始有终地拿下。