在上一篇中，我们提到了二项分布，并且指出：
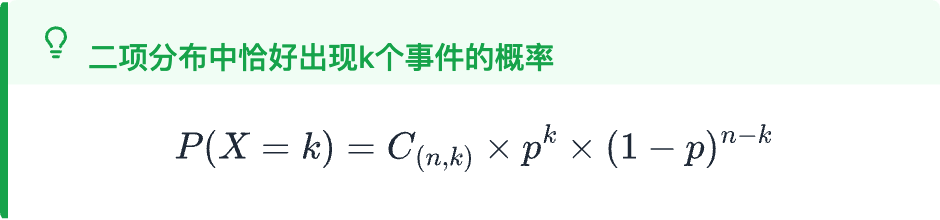
二项分布究竟意味着什么呢？ 实际上，有一个名为 Galton Board 的装置，可以很好地可视化它的含义：
图1 高尔顿板
具体来说，高尔顿板是一块竖直木板，顶部有一个小球入口，下方有等距的垂直隔板，形成多个凹槽；木板中间钉满了等间距的钉子，呈三角形排列（每一层钉子比上一层多一个，且与上层钉子错开，呈 Pascal 三角或者杨辉三角分布）。
当我们把小球从入口扔进木板时，小球会碰到中间的钉子，然后会向左或者向右弹开，直到碰到下一个钉子或者掉落到下方的垂直隔板。通过每个凹槽里落入的小球数量与小球总数之比，我们就可以知道小球在 n 次碰撞中，连续 k 次选择『右』或者『左』的概率。
实际上，Galton Board 装置的下半部分，正好就是我们在统计学中，常常会用到的直方图。凹槽的宽度可视为 "组距"，凹槽的高度（小球堆积的高度）则对应 "频率"。只不过，在绘制直方图时，我们可以任意指定组距。
在这样一个装置中，如果钉子数越来越多，试验次数也越来越多，会发生什么情况呢？下图显示了在有20层钉子，试验500次时的一种可能结果：
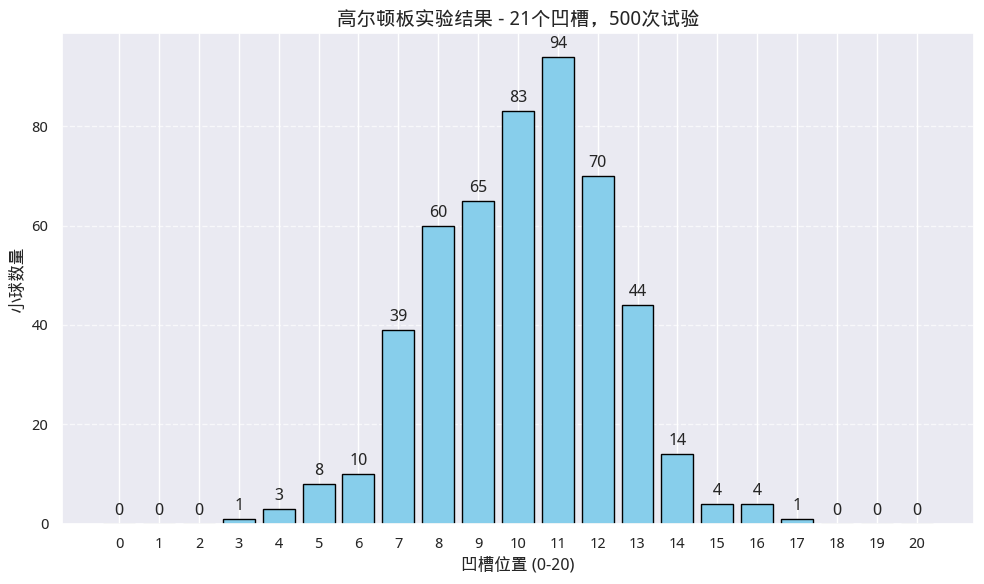
在这个图中，如果我们把每一个凹槽按位置进行编号，把小球落入的位置看成事件的取值，那么我们就得到了一个离散型的随机变量。在图2中，它的取值区间是[0, 20]。
如果我们增加层数，多试验几次，又会如何？下图显示了1000个凹槽、1百万次试验的一种可能结果：
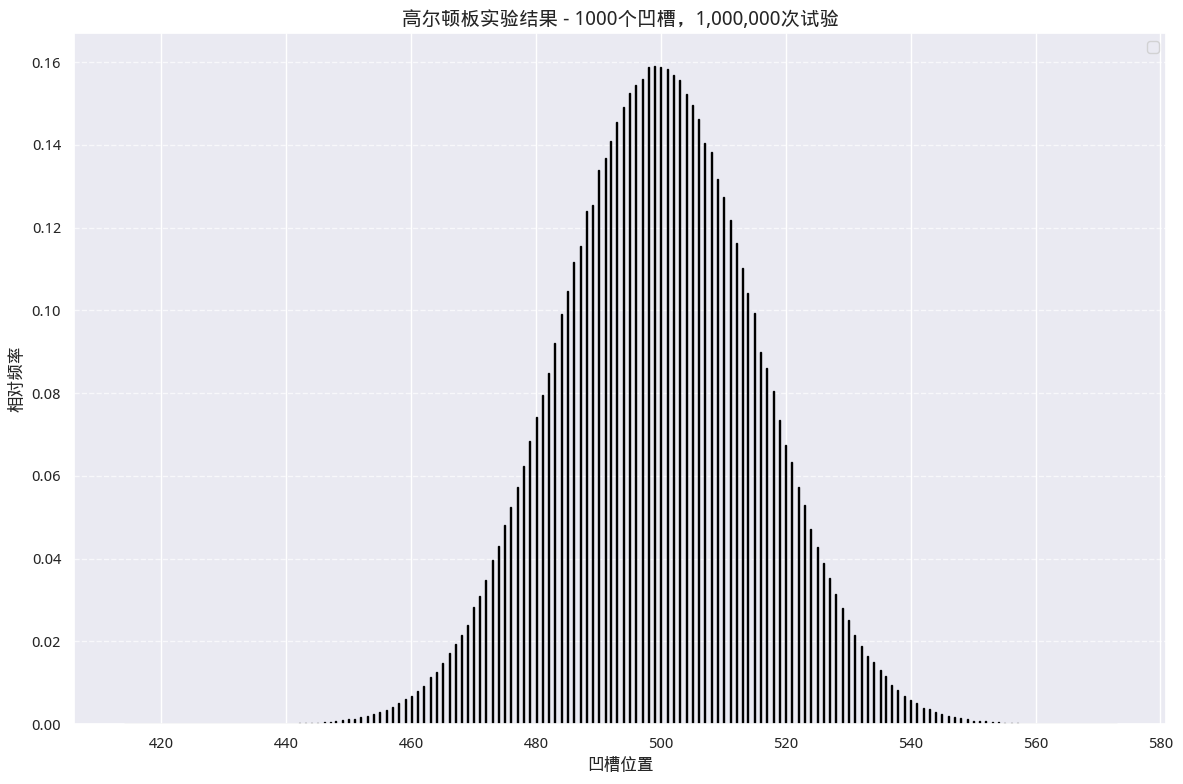图3 频率/随机变量图
我们看到随机变量的中心值是500左右 -- 说明我们的实验是正确的，因为凹槽的个数是1000。但最小值与最大值并不是0和1000，这是因为我们试验的次数还不够多，要使得二项分布取到这样的极限值还是非常困难的。但是，如果凹槽的个数只有10个，而试验次数达到1000次，就很容易取到（0， 10）这两个极值了。
或许你已经注意到，这次的图跟图2有一点不一样。这次我们绘制的实际上不再是直方图，而是概率密度/随机变量图。我们用来绘制这张图的代码是：
python
import matplotlib.pyplot as plt
plt.hist(positions, bins=num_grooves, density=True)这里的关键参数是 density=True。当指定它为 True 时，直方图绘制函数 hist 绘制的 y 轴就不再是每一个箱的频数，而是概率密度。
这个概率密度是这样算的。在图3中，我们要求把落在大致范围(428, 575)内的随机数，按1000个分箱进行平均分组，这样得到组距大约在0.147的箱子共1000个。每个箱子里落到的随机数（小球个数），计作 X i X_i Xi，则 X i n × 0.147 \frac{X_i}{n \times 0.147} n×0.147Xi 就是 X X X 在这个分箱中的概率密度。按几何概率的求法，这个概率密度乘以分箱长度 -- 即小矩形的面积 -- 就得到了小球落在该区间的概率。
显然，这1000个矩形的面积之和应该等于1。因为它就是所有事件发生的概率之和。如果我们问，随机变量 X 小于500的概率是多少？那就是把从左到右，前500个矩形的面积加起来。
如果我们继续扩大凹槽数量和试验次数，比如说凹槽增加到1万个呢？最终，每个分箱和它们对应的概率密度在图上会紧挨在一起，从而在视觉上无法将其分开，我们将得到下面的图：
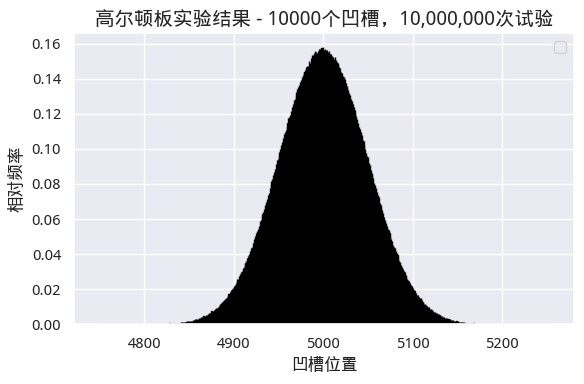图4 趋近于正态分布
但是，这张图仍然是由若干个矩形组成的。对于任意一个 X i X_i Xi，我们都能通过计算前 i i i个矩形的面积和，来算出 X ≥ X i X \ge X_i X≥Xi的概率。尽管矩形个数增加了，但所有的小矩形的面积和仍然为1。
如果我们继续加大钉子的层数和试验次数，使得它们都趋向于 + ∞ +\infty +∞呢？这时候，不仅仅是矩形从屏幕上消失，它们实际上在物理意义上也不构成矩形了。这时候我们只会看到屏幕上一条平滑的钟形曲线。
在这个趋向于无穷大的过程中，会发生什么呢？在 Galton Board 中，随机变量的取值（小球能落入的凹槽位置）是有限的，是离散值。而当 n n n 和钉子层数（实际上也就是凹槽个数）趋向于无穷大时，随机变量的取值也将由离散值变为连续值。
现在，再来求事件 X ≥ X i X \ge X_i X≥Xi的概率，我们就无法通过小矩形的面积和来计算了。不过，当小矩形的长度趋近于零时，求和正好是积分的含义。于是，我们就得到积分表示的分布函数。
PDF 和 CDF
在前面的讨论中，我们已经接触到了 PDF （Probability Density Function）和 CDF（Cumulative Distribution Function）。前者被翻译成为概率密度函数，后者被翻译成为累积分布函数，常常也被简称为分布函数。
显然，从前面的介绍中，我们发现，CDF 是 PDF 的积分，那么 PDF 就是 CDF 的导数。我们有以下公式：
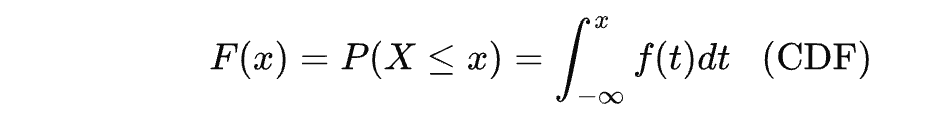
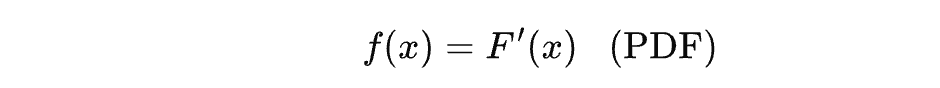
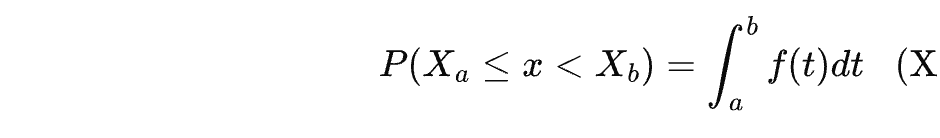
因此，PDF 是 CDF 的一阶导数，反映了 CDF 在某点的变化率。而 CDF 是指随机变量的取值小于或等于 x x x 的概率。
为了理解 CDF 与 PDF 的计算，我们举一个简单的例子，均匀分布的概率密度函数。
假设随机变量 X 在区间 [ 0 , n ] [0,n] [0,n]上均匀分布，则概率密度为 f ( x ) = 1 n f(x) = \frac{1}{n} f(x)=n1，概率分布函数为 F ( x ) = x n F(x) = \frac{x}{n} F(x)=nx。
此时，要求随机变量 X 落在区间 a,b 上的概率是：
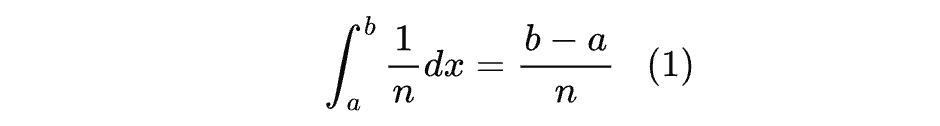
为了帮助大家理解，作为量化人，这里举一个量化场景下的例子。这个例子在『量化24课』中详细讲解过。
概率密度函数只适用于连续型随机变量。这当然是对的，因为 PDF 与 CDF 之间是积分与导数的关系，所以，PDF 概念对离散型随机变量自然就不适用了。
期望
上一期『PDF is all you need』发表之后，有同学问，可不可以讲一点博彩概率（大意是这样？）。我对这些名词都不太懂。不过，大致上应该是跟期望有关的东西。
因为在博弈中，期望（Expected Value） 是分析策略选择、评估局势优劣的核心工具，尤其适用于存在不确定性（如对手策略、随机结果）的博弈场景。其核心逻辑是：通过计算不同策略的期望收益（或损失），选择能最大化自身利益（或最小化风险）的最优策略。
期望（又称均值）是随机变量取值的加权平均值，权重是每个取值对应的概率。
期望一般用符号 E ( x ) E(x) E(x) 来表示。X 是随机变量。如果 X 是离散的，那么期望是"每种结果的取值 × 该结果发生的概率"之和，即：
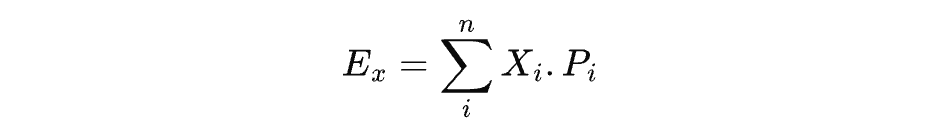
这里 X i X_i Xi是第 i i i种结果， P i P_i Pi是对应的概率。
对于连续情况，期望的求法要难懂不少。由于对于 X i X_i Xi，不存在对应的概率，只有对应的概率密度，因此期望要通过积分来计算，即：
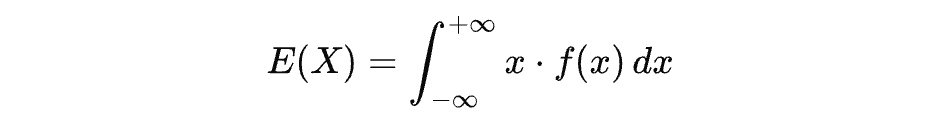
它可以理解成为概率密度函数（PDF）曲线与坐标轴转成的『加权面积』，本质上，相当于计算一个特殊图形的质心。
我们可以通过下面的代码，把『加权面积』和『重心』都绘制出来。
python
# 因为篇幅原因，仅保留关键语句。学员可得完整 notebook
mu, sigma = 5, 1
# 定义 X，pdf, x·f(x)
x_norm = np.linspace(mu - 3 * sigma, mu + 3 * sigma, 1000)
y_norm_pdf = norm.pdf(x_norm, mu, sigma)
y_norm_g = x_norm * y_norm_pdf
mask = x_norm <= 6
plt.plot(x_norm, y_norm_pdf, "b-", label=f"正态分布PDF")
# 计算第一个子图中到x=6的积分值（累积概率）
integral_pdf_up_to_6 = np.trapezoid(y_norm_pdf[mask], x_norm[mask])
# 计算期望
E = np.trapezoid(y_norm_g, x_norm)
plt.axvline(E, color="green", linestyle="-", label=f"期望= {E:.2f}")
# 计算子图1中，到 X=6 时的重心
area = np.trapezoid(y_norm_g[mask], x_norm[mask])
centroid = area / integral_pdf_up_to_6
plt.plot(x_norm, y_norm_g, "r-", label="g(x) = x·f(x)")
# 只填充到x=6的区域
plt.fill_between(x_norm[mask], y_norm_g[mask], alpha=0.3, color="red")
# 计算第二个子图中到x=6的积分值
integral_g_up_to_6 = np.trapezoid(y_norm_g[mask], x_norm[mask])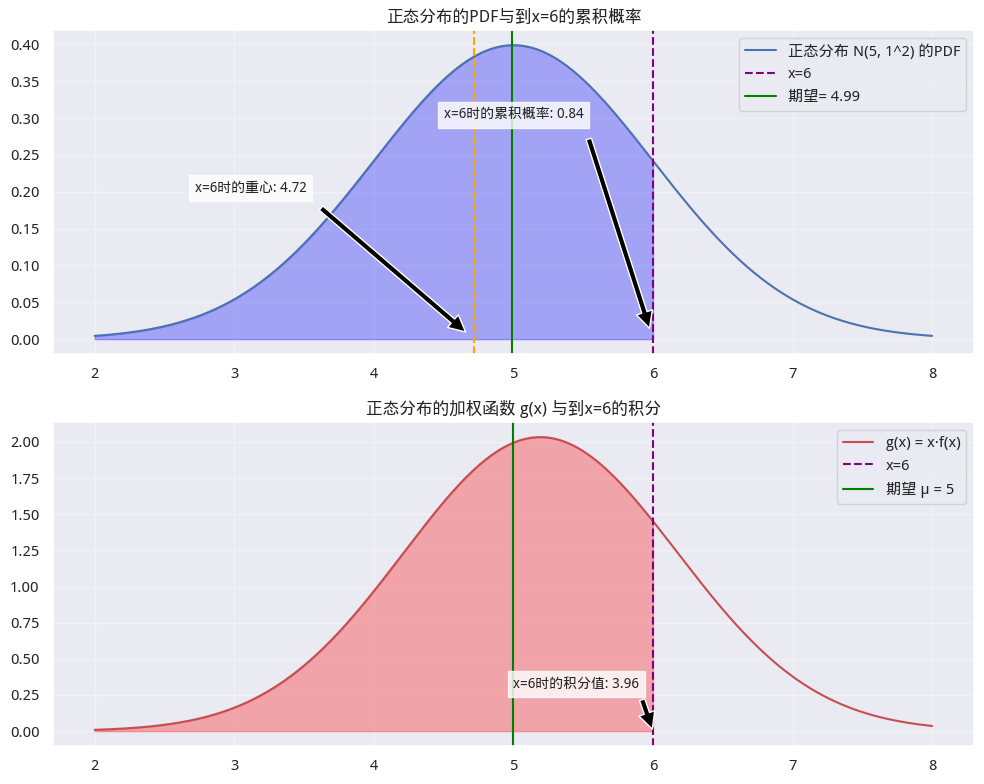
图5 正态分布与期望
第一个子图是正态分布的密度函数图。它的积分是分布函数。当 x = 6 x=6 x=6时， P ( X ≤ x ) = 0.84 P(X\leq x)=0.84 P(X≤x)=0.84。理论期望是5，实际计算出来的值（第14行代码）为4.99。
如果把正态分布密度函数图理解成为一座天秤，那么 μ \mu μ的位置就正好在天秤的正中间，这就是期望是分布的重心说法的来由。
第二个子图是对 g ( x ) = x . f ( x ) g(x) = x.f(x) g(x)=x.f(x)的积分。当 x = 6 x = 6 x=6时， g ( x ) g(x) g(x)的积分为3.96。此时对应的分布的积分为0.84，因此， g ( x ) g(x) g(x)的重心为 3.96 / 0.84 = 4.72 3.96/0.84 = 4.72 3.96/0.84=4.72。
我们把这个重心（线）也画在了图5中的第一个子图上。它是最左侧的橘色竖线。直觉上看，它确实是在 PDF 函数、随机变量 X 与竖线 X=6 围成的区域的几何中心上。
如果看了这么多，你还是感觉难以理解期望的积分算法，你可以尝试把 x x x或者 f ( x ) f(x) f(x)看成一个常量，常量可以提取到积分式以外，这样就变成了一个简单积分--在物理意义上有更直观理解的东西。
『高阶』期望
在前面介绍的期望公式中，我们求得的是随机变量 X X X 的期望：
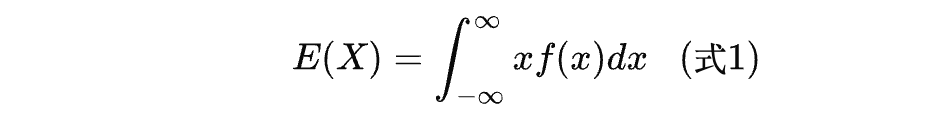
你可能要问，式子中的第一个 x x x 为何这样特殊？如果它本身也是一个函数，则式子：
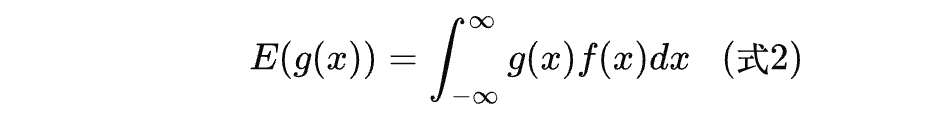
有何含义？
首先，如果 g ( x ) = x g(x) = x g(x)=x，则式子（2）就退化为式子（1），即都是在求随机变量 X X X的期望。如果 g ( x ) = 1 g(x) = 1 g(x)=1，则式子2还成为分布函数。
一般地，只要我们看到某个函数乘以概率密度再积分，那么它就是对该函数的期望。这就是式子2的含义。
这种推广有何意义？ 我们知道，离散随机变量是没有 PDF 的。但是，如果离散随机变量 g ( x ) g(x) g(x)本身是一个分段函数，而在每一个分段区间，都存在着概率密度函数呢？
此时，式2本质上是对随机变量函数 g ( X ) g(X) g(X)进行加权平均，权重由 X 的概率密度 f ( x ) f(x) f(x) 决定，它就成为离散型期望在连续场景下的自然推广，是计算连续型随机变量函数平均值的基础工具。
n 个点共半圆问题
有了这些知识铺垫之后，让我们再回到本系列第一篇中提出的问题：
现在，我们可以用以下递归模型来求解此问题：
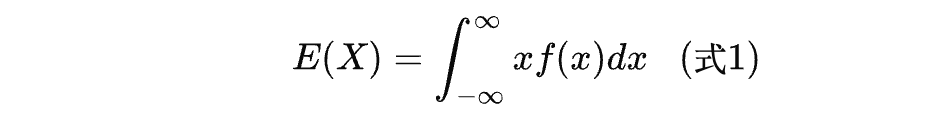
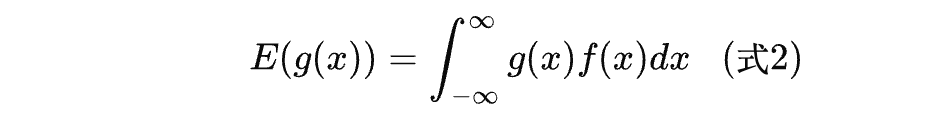
这里， P n P_n Pn表示随机放置的 n 个点全部落在同一个半圆内的概率。同理， P n − 1 P_{n-1} Pn−1是 n − 1 n-1 n−1 个点全部落在同一个半圆内的概率。
X n X_n Xn是事件，表明第 n n n个点与前 n − 1 n-1 n−1个点同落在同一个半圆内。
P ( X n ∣ P n − 1 ) P(X_n|P_{n-1}) P(Xn∣Pn−1)表示在前 n − 1 n-1 n−1个点已经落在同一个半圆内的条件下，第 n n n个点也落在同一个半圆内的概率。
α n − 1 \alpha_{n-1} αn−1 表示在前 n − 1 n-1 n−1个点共半圆时，它们所能张出的最大夹角（即这 n − 1 n-1 n−1个点在半圆内分布时，最外侧两个点之间的圆心角，取值范围为 ( 0 , 2 π ) (0, 2\pi) (0,2π)。它也是一个随机变量。
f α n − 1 ( x ) f_{\alpha_{n-1}}(x) fαn−1(x)：随机变量 α n − 1 \alpha_{n-1} αn−1的概率密度函数，表示 α n − 1 \alpha_{n-1} αn−1取值为 x x x时的概率密度。
P ( X n ∣ α n − 1 = x ) P(X_n | \alpha_{n-1}=x) P(Xn∣αn−1=x)：在前 n − 1 n-1 n−1个点的最大夹角为 x x x的条件下，第n个点能与它们共半圆的概率。
式3）很容易理解，它是用递推公式来表示第 n n n个点共圆的概率。它的逻辑是，只有前 n − 1 n-1 n−1个点先共半圆，才有可能让第n个点加入并形成n个点共半圆的情况，因此是递归依赖关系。
式4）是全概率公式的连续形式。它的含义是，基于全概率公式，对连续随机变量 α n − 1 \alpha_{n-1} αn−1的所有可能取值 x x x进行加权积分。权重为 α n − 1 = x \alpha_{n-1}=x αn−1=x的概率密度 f α n − 1 ( x ) f_{\alpha_{n-1}}(x) fαn−1(x)，被加权项为该条件下第 n n n个点能共半圆的概率 P ( X n ∣ α n − 1 = x ) P(X_n | \alpha_{n-1}=x) P(Xn∣αn−1=x)。
这里的表述尽管很复杂，但是，它的严谨性不言自明。在一下篇，我们将对它进行推导求解。这个过程，将把所有的知识（PDF 和期望），以及归纳法串起来。
