一篇文章入门主成分分析PCA

文章目录

基本概念
主成分分析

基本概念

事件

事件：某种情况的"陈述" ⇒ \Rightarrow ⇒ 事件A：掷出的骰子为偶数点 ⇒ \Rightarrow ⇒ 事件A包含多种结果，每种结果都是一个基本事件 ⇒ \Rightarrow ⇒ 事件的本质是集合

事件之间的基本关系：

蕴含与相等：如果当A发生时B必发生 ，记数学公式: A ⊂ B A \subset B A⊂B数学公式: ⇒ \Rightarrow ⇒当数学公式: A , B A,B A,B相互蕴含时，两式相等，记数学公式: A = B A=B A=B
互斥与对立：在一次试验中不可能同时发生，但可以都不发生 ，有A就没有B，有B没有A，但是可以同时没有A和B数学公式: ⇒ \Rightarrow ⇒A为一事件，则事件 B={A不发生} ，则A和B互为对立事件
事件和（或称并集）：A和B中至少发生一个(并集) ，记数学公式: C = A + B C=A+B C=A+B
事件积（或称交集）：A发生且B发生（交集） ，记数学公式: C = A B C=AB C=AB
事件差：A发生且B不发生 ，记数学公式: C = A − B C=A-B C=A−B

全概率公式：一个事件的概率，该事件可以表示为若干互斥事件的联合

随机变量

随机变量是实验结果的函数 ⇒ \Rightarrow ⇒抛一枚硬币，定义1=正面朝上，0=反面朝上，所以随机变量 X X X就代表抛硬币这个试验的结果，要么0要么1

独立同分布

独立性：一个随机变量的取值不会影响另一个随机变量的取值

同分布：所有随机变量服从相同的概率分布

离散型随机变量

伯努利分布（两点分布）

伯努利分布：两种可能结果的实验（如成功和失败） ，成功的概率为 p p p，失败的概率为 1 − p 1-p 1−p

概率密度函数： P ( X = x ) = { p if x = 1 1 − p if x = 0 P(X=x)=\begin{cases}p&\text{if}\ \ x=1\\1-p&\text{if}\ \ x=0\end{cases} P(X=x)={p1−pif x=1if x=0

期望值： E ( X ) = p E(X)=p E(X)=p

方差： V a r ( X ) = p ( 1 − p ) Var(X)=p(1-p) Var(X)=p(1−p)

二项分布

二项分布：n次独立同分布的伯努利试验的成功次数的分布 ，每次试验成功的概率为 p p p 概率密度函数： P ( X = k ) = ( n k ) p k ( 1 − p ) n − k P(X=k)=\binom{n}kp^k(1-p)^{n-k} P(X=k)=(kn)pk(1−p)n−k

期望值： E ( X ) = n p E(X)=np E(X)=np

方差： V a r ( X ) = n p ( 1 − p ) Var(X)=np(1-p) Var(X)=np(1−p)

几何分布

几何分布：在第一次成功之前的失败次数（包括第一次成功） ，每次试验成功的概率为 p p p

概率密度函数： P ( X = k ) = ( 1 − p ) k p for k = 0 , 1 , 2 , ... P(X=k)=(1-p)^kp\quad\text{for}\ \ k=0,1,2,\ldots P(X=k)=(1−p)kpfor k=0,1,2,...

期望值： E ( X ) = 1 − p p E(X)=\frac{1-p}p E(X)=p1−p

方差： Var ⁡ ( X ) = 1 − p p 2 \operatorname{Var}(X)=\frac{1-p}{p^2} Var(X)=p21−p

泊松分布

泊松分布：单位时间或空间内某事件的发生次数 ，在一个间隔中平均发生事件的次数由 λ \lambda λ决定， λ \lambda λ是事件发生比率

概率密度函数： P ( X = k ) = λ k e − λ k ! P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!} P(X=k)=k!λke−λ

期望值： E ( X ) = λ E(X)=\lambda E(X)=λ

方差： Var ⁡ ( X ) = λ \operatorname{Var}(X)=\lambda Var(X)=λ

"事件"可理解为一天中网站的访客数、一天中所接到的电话数

例如：每周平均有15个人给我的博客点赞，我想预测下一周的点赞数

如果使用二项分布来解决，令 x x x表示在 n n n次重复实验中发生点赞的次数， p p p表示每次实验的点赞概率(Probability)。我们现在已知的是每周平均的点赞比率(rate)为15个赞/周，并不知道点赞概率 p p p和博客访客数 n n n的任何信息

假设过去的1年(=52周)的数据中，一共有 10000 10000 10000人看了我的博客，其中有 800 800 800个人点赞了，这样平均每周访客数 = 10000 / 52 = 192 =10000 / 52 = 192 =10000/52=192，平均每周点赞数 = 800 / 52 = 15 =800 / 52 = 15 =800/52=15，可得到概率 p = 800 / 10000 = 0.08 = 8 % p = 800 / 10000 = 0.08 = 8 \% p=800/10000=0.08=8%

使用二项分布的概率密度函数，预测下一周有20个人点赞的概率为： B i n ( m = 20 ∣ N = 192 , p = 0.08 ) = N ! ( N − m ) ! m ! p m ( 1 − p ) N − m = 0.04657 \mathrm{Bin(m=20\mid N=192,p=0.08)=\frac{N!}{(N-m)!m!}p^m(1-p)^{N-m}=0.04657} Bin(m=20∣N=192,p=0.08)=(N−m)!m!N!pm(1−p)N−m=0.04657

在上述过程中，可以将x=该周有15次点赞，也可以是x=该天有 15 / 7 = 2.1 15/7=2.1 15/7=2.1个赞，也可以是x=该小时有 15 / 7 ∗ 24 = 0.1 15/7*24=0.1 15/7∗24=0.1个赞，这意味着大多数小时没有赞，而有的小时有一个点赞。仔细想想，似乎一定时间内出现超过1个点赞的情况也是合理的（比如文章早上刚发布的时候）。由此，二项分布的问题是它无法在一个时间单元中包含超过1次的事件 （在这里，时间单元是1小时）

那么，我们将1小时切分成60分钟，时间单元是1分钟，使得1小时能够包含多个事件。问题得到解决了吗？还没有，比如何同学的5G视频，一晚上点赞就过百万，1分钟内不止一个赞。那我们再将时间单元切分成秒，这样1分钟又能包含多个事件。这样思考下去，我们会将已有的事件单元不断地切分，直到满足一个时间单元只包含一个事件，而大的时间单元能够包含1个以上的事件

形式化来看，这意味着 n → ∞ n\to \infty n→∞，当我们假定比率(rate)固定，则必须让 p → 0 p\to 0 p→0，否则点赞数 n × p → ∞ n \times p \to \infty n×p→∞

基于以上的约束，时间单元变得无穷小。我们不用担心同一个时间单元包含一个以上的事件了

在用二项分布时，无法直接用比率(rate)来计算点赞概率 p p p，而是需要 n n n和 p p p才能使用二项分布的概率密度函数，而泊松分布不需要知道 n n n和 p p p，它假定 n n n是一个无穷大的数，而 p p p是无穷小的数，泊松分布唯一参数是比率 λ \lambda λ。现实中，得知 n n n和 p p p得进行很多次实验，而短时间内，比率（rate）很容易得到（例如，在下午2点-4点，收到了4个点赞）

泊松分布的假设：每个时间单元的事件平均发生比率是常数

例如：博客的每小时平均点赞数不太可能服从泊松分布，而博客每个月的平均点赞数可近似看作是固定的。假如你的博客写的很好，被公众号转发推广了，那可能会有大批的读者来阅读，这种情况下的点赞数就不满足泊松分布了

泊松分布的适用条件：

事件独立性：事件的发生是相互独立的，例如，每个读者对文章的点赞行为不受其他读者行为的影响
事件发生概率相等：每个事件在单位时间或空间内发生的概率是相同的
单位时间或空间内事件的发生率固定 ：单位时间或空间内事件的平均发生次数（ λ \lambda λ）是固定的

当博客被公众号转发推广后，会出现以下变化：

读者行为不再独立：由于公众号转发，读者可能会集中在某个时间段内大量访问博客，导致点赞行为之间不再独立。例如，一个读者点赞后，可能会引起更多读者来点赞，这种情况下点赞行为具有相关性
事件发生概率不再相等：在被转发推广的时段，点赞的概率可能会显著提高，导致某些时间段内的点赞率远高于平时
事件发生率不固定：被推广后，单位时间内的访问量和点赞量会显著增加，不再符合泊松分布所要求的固定事件发生率

连续型随机变量

正态分布

概率密度函数： f ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 f(x)=\frac1{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ2 1e−2σ2(x−μ)2

期望值： E ( x ) = μ E(x)=\mu E(x)=μ

方差： Var ⁡ ( X ) = σ 2 \operatorname{Var}(X)=\sigma^2 Var(X)=σ2

期望

期望是随机变量取值的平均，以概率为权重对随机变量进行加权求和

平均数是对一组已经观察到的样本进行统计的量
由于概率是频率随样本趋于无穷的极限，所以期望其实就是平均数随样本趋于无穷的极限，两者是通过大数定理联系起来的

离散型随机变量的期望值 E ( X ) \mathrm{E}(X) E(X)： E ( X ) = ∑ i x i P ( X = x i ) \mathrm{E}(X)=\sum_ix_iP(X=x_i) E(X)=∑ixiP(X=xi)
连续型随机变量的期望值 E ( X ) \mathrm{E}(X) E(X)： E ( X ) = ∫ − ∞ ∞ x f X ( x ) d x E(X)=\int_{-\infty}^\infty xf_X(x) dx E(X)=∫−∞∞xfX(x)dx

期望的性质：

E ( X 1 + X 2 + ⋯ + X n ) = E ( X 1 ) + E ( X 2 ) + ⋯ + E ( X n ) \mathrm{E}\left(\mathrm{X}_1 +\mathrm{X}2 + \cdots +\mathrm{X}\mathrm{n}\right)=\mathrm{E}\left(\mathrm{X}_1 \right)+\mathrm{E}\left(\mathrm{X}2 \right)+ \cdots+\mathrm{E}\left(\mathrm{X}\mathrm{n} \right) E(X1+X2+⋯+Xn)=E(X1)+E(X2)+⋯+E(Xn)（无条件成立）
E ( X 1 X 2 ⋯ X n ) = E ( X 1 ) E ( X 2 ) ⋯ E ( X n ) \mathrm{E}(X_1 X_2 \cdots X_n) = \mathrm{E}(X_1 ) \mathrm{E} (X_2 ) \cdots \mathrm{E} (X_n ) E(X1X2⋯Xn)=E(X1)E(X2)⋯E(Xn)（独立情况下成立）

方差

方差是用来衡量随机变量和其数学期望之间的偏离程度的量，方差越大，那么这一组数据的波动幅度也就越大

因为 X X X是随机的，所以偏离的量 X − E X X-EX X−EX本身也是随机的，为了避免正负相互抵消，对其取平方作为偏离量，很自然方差就是该偏离量的期望，定义为： V a r ( X ) = E ( X − E X ) 2 = E ( X 2 ) − ( E X ) 2 \mathrm{Var(X)=E(X-EX)^2=E\left(X^2\right)-(EX)^2} Var(X)=E(X−EX)2=E(X2)−(EX)2

假如给定一个含有 n n n个样本的集合，则方差计算为： σ 2 = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 \mathrm{\sigma^2=\frac{\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}{n-1}} σ2=n−1∑i=1n(Xi−Xˉ)2

之所以除以n-1而不是除以n，是因为我们是用样本去估计总体，除n-1才是统计学上的"无偏估计" ，这样能使我们以较小的样本集更好的逼近总体的标准差

方差的性质：

常数的方差为 0 0 0
若 C C C为常数，则 V a r ( X + C ) = V a r ( X ) \mathrm{Var(X+C)=Var(X)} Var(X+C)=Var(X)
若 C C C为常数，则 V a r ( C X ) = C 2 V a r ( X ) \mathrm{Var(CX)=C^2Var(X)} Var(CX)=C2Var(X)
独立情况下， V a r ( X 1 + ⋯ + X n ) = V a r ( X 1 ) + ⋯ + V a r ( X n ) \mathrm{Var\left(X_1\right.+\cdots+X_n})=\mathrm{Var\left(X_1)\right.}+\cdots+\mathrm{Var\left(X_n\right)} Var(X1+⋯+Xn)=Var(X1)+⋯+Var(Xn)

标准化

标准化可以使每个样本的均值为0、标准差为1： x ′ = x − x ˉ σ \mathrm x'=\frac{\mathrm x-\bar{\mathrm x}}\sigma x′=σx−xˉ

协方差

协方差衡量两个随机变量之间的线性关系

对于两个随机变量 X X X和 Y Y Y，协方差的定义为 Cov ⁡ ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] = E ( X Y ) − E ( X ) E ( Y ) \operatorname{Cov}(X,Y)=E\left[(X-E(X))(Y-E(Y))\right]=E(XY)-E(X)E(Y) Cov(X,Y)=E[(X−E(X))(Y−E(Y))]=E(XY)−E(X)E(Y)

正协方差：如果 Cov ⁡ ( X , Y ) > 0 \operatorname{Cov}(X,Y)>0 Cov(X,Y)>0，则表明 X X X和 Y Y Y之间存在正的线性关系
负协方差：如果 Cov ⁡ ( X , Y ) < 0 \operatorname{Cov}(X,Y)<0 Cov(X,Y)<0，则表明 X X X和 Y Y Y之间存在负的线性关系
零协方差：如果 Cov ⁡ ( X , Y ) = 0 \operatorname{Cov}(X,Y)=0 Cov(X,Y)=0，则表明 X X X和 Y Y Y之间没有线性关系 ⇒ \Rightarrow ⇒零协方差并不意味着 X X X和 Y Y Y完全不相关，它们可能存在非线性的关系

假设数据矩阵 X X X的大小为 n × p n\times p n×p，其中 n n n是样本数， p p p是特征数， X X X的每一行代表一个样本，每一列代表一个特征

给定数据矩阵 X X X，协方差矩阵的计算公式为： Σ = 1 n − 1 X T X \Sigma=\frac{1}{n-1}X^TX Σ=n−11XTX
X T X X^TX XTX是一个 p × p p\times p p×p的矩阵，表示各特征之间的内积和

线性组合

线性组合：设 β , α 1 , α 2 , . . . , α n \mathrm{\beta} , \alpha_{1} , \alpha_{2} , ..., \alpha_{\mathrm{n}} β,α1,α2,...,αn是一组 m m m维向量，若存在数 k 1 , k 2 , . . . , k n \mathrm{k_{1} , k_{2} , ...,k_{n}} k1,k2,...,kn，使得 β = k 1 α 1 + k 2 α 2 + . . . + k n α n \mathrm{\beta=k_1\alpha_1~+k_2\alpha_2~+~...~+k_n\alpha_n} β=k1α1 +k2α2 + ... +knαn，则称 β \beta β是向量组 α 1 , α 2 , . . . , α n \alpha_{1} , \alpha_{2} , ..., \alpha_{\mathrm{n}} α1,α2,...,αn的线性组合， k 1 , k 2 , . . . , k n \mathrm{k_{1} , k_{2} , ...,k_{n}} k1,k2,...,kn为一组组合系数

性质：

零向量可由任意向量组来线性表示 ： 0 = 0 α 1 + 0 α 2 + . . . + 0 α n \mathbf{0}=0\alpha_1+0\alpha_2+...+0\alpha_\mathrm{n} 0=0α1+0α2+...+0αn
向量组中任意一个向量可由向量组来线性表示 ： α 3 = 0 α 1 + 0 α 2 + 1 α 3 + 0 α 4 \alpha_3=0\alpha_1+0\alpha_2+1\alpha_3+0\alpha_4 α3=0α1+0α2+1α3+0α4
任意一个向量都可由基向量 ε 1 = ( 1 , 0 , . . . , 0 ) , ε 2 = ( 0 , 1 , . . . , 0 ) , . . . , ε n = ( 0 , 0 , . . . , 1 ) \begin{aligned}\varepsilon_1& =(1,0,...,0),\varepsilon_2 =(0,1,...,0),...,\varepsilon_\text{n} =(0,0,...,1)\end{aligned} ε1=(1,0,...,0),ε2=(0,1,...,0),...,εn=(0,0,...,1)来线性表示： ( 1 , 2 , 3 ) = 1 × ( 1 , 0 , 0 ) + 2 × ( 0 , 1 , 0 ) + 3 × ( 0 , 0 , 1 ) (1,2,3)=1\times(1,0,0)+2\times(0,1,0)+3\times(0,0,1) (1,2,3)=1×(1,0,0)+2×(0,1,0)+3×(0,0,1)
设 β = ( − 3 , 2 , − 4 ) , α 1 = ( 1 , 0 , 1 ) , α 2 = ( 2 , 1 , 0 ) , α 3 = ( − 1 , 1 , − 2 ) \beta = (-3,2,-4), \alpha_{1} = (1,0,1), \alpha_{2} = (2,1,0), \alpha_{3} =(-1,1,-2) β=(−3,2,−4),α1=(1,0,1),α2=(2,1,0),α3=(−1,1,−2)，判断 β \beta β是否可由 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α2,α3线性表示？

特征值和特征向量

特征向量表示变换的方向，特征值表示在每个方向上的伸缩程度

特征值分解

相似矩阵：设 A , B A,B A,B都是 n n n阶矩阵，若有可逆矩阵 P P P，使 P − 1 A P = B \mathrm{P}^{-1}\mathrm{AP}=\mathrm{B} P−1AP=B，则称 A A A与 B B B相似，这个过程称为相似变换， P P P为相似变换矩阵

如果 A A A与对角矩阵 Λ = ( λ 1 λ 2 ⋱ λ n ) \left.\boldsymbol{\Lambda}=\left(\begin{array}{rrrrr}\lambda_{1}&&&&\\&\lambda_{2}&&&\\&&\ddots&&\\&&&\lambda_{\mathrm{n}}&\end{array}\right.\right) Λ= λ1λ2⋱λn 相似，即 P − 1 A P = Λ \mathrm{P}^{-1}\mathrm{AP}=\Lambda P−1AP=Λ，那么 λ 1 , λ 2 , ⋯ , λ n \lambda_{1},\lambda_{2} ,\cdots ,\lambda_{\mathrm{n}} λ1,λ2,⋯,λn是 A A A的 n n n个特征值，而 P P P的列向量 p i p_i pi就是 A A A对应于特征值 λ i \lambda_i λi的特征向量

把 P P P乘到右边，得到： A = P Λ P − 1 \mathrm A=\mathrm P\Lambda\mathrm P^{-1} A=PΛP−1这个式子就是实际中经常用到的特征值分解，一个矩阵 A A A可以通过特征值分解得到它的特征值和特征向量

对称矩阵的特征值分解

对称矩阵： A T = A \mathrm{A^{T}}=\mathrm{A} AT=A ⇒ \Rightarrow ⇒对称矩阵有 N N N个线性无关的特征向量，且不同特征值对应的特征向量相互正交
对称矩阵一定可以相似对角化 ，故实对称矩阵 A A A可以被分解成： A = P Λ P − 1 = P Λ P T \mathrm{A}=\mathrm{P} \Lambda\mathrm{P}^{-1}=\mathrm{P} \mathrm{\Lambda}\mathrm{P}^{\mathrm{T}} A=PΛP−1=PΛPT，其中 P P P为正交矩阵（ P P T = E \mathrm{PP}^{\mathrm{T}}=\mathrm{E} PPT=E）

齐次线性方程组

齐次线性方程组是指所有常数项（即方程的右端）都等于零的线性方程组 ： A x = 0 A\mathbf{x}=\mathbf{0} Ax=0，其中 A A A是一个 m × n m\times n m×n的矩阵， x \mathbf{x} x是一个 n n n维列向量， 0 \mathbf{0} 0是一个 m m m维列向量

单位向量

单位向量是指长度为1的向量 ，在欧几里得空间中，如果向量 u \mathbf{u} u满足 ∥ u ∥ = 1 \|\mathbf{u}\|=1 ∥u∥=1，其中 ∥ u ∥ \|\mathbf{u}\| ∥u∥表示向量 u \mathbf{u} u的长度，则 u \mathbf{u} u是一个单位向量

基向量

基向量是向量空间的一组向量，通过线性组合这些向量可以表示空间中的任何向量，向量空间中的基向量通常是线性无关的

矩阵的秩

矩阵的秩（Rank）是其行向量的最大线性无关组的数量

从几何角度来看，矩阵的秩表示由矩阵的行向量生成的向量空间的维数，对于一个 3 × 3 3\times3 3×3的矩阵：

如果其秩为 3，表示其行向量是三维空间的基，可以生成整个三维空间
如果秩为 2，表示行向量位于同一平面，且可以生成一个二维平面
如果秩为 1，表示所有行向量都在同一条直线上

对于方阵，如果其行列式不为零，则该矩阵是满秩矩阵，即秩等于矩阵的阶数。反之，如果行列式为零，则矩阵的秩小于其阶数

最高阶非零子式

一个 k × k k\times k k×k子式是从矩阵中选取 k k k行和 k k k列形成的一个 k × k k\times k k×k方阵的行列式
最高阶非零子式是指在所有非零子式中，阶数最高的那个子式

假设有一个 3 × 3 3\times 3 3×3矩阵： A = ( 1 2 3 4 5 6 7 8 9 ) A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix} A= 147258369

正定矩阵

正定矩阵是一种特殊的实对称矩阵

实对称矩阵：矩阵的转置等于其自身的矩阵，对于任意 i i i和 j j j，其第 i i i行第 j j j列的元素等于第 j j j行第 i i i列的元素

一个实对称矩阵 A A A 被称为正定的，如果对于任意非零向量 x x x，都有 x T A x > 0 x^TAx>0 xTAx>0

一个实对称矩阵 A A A被称为半正定的，如果对于任意非零向量 x x x，都有 x T A x ≥ 0 x^TAx\geq0 xTAx≥0

正交矩阵

正交矩阵的逆矩阵和转置矩阵是相同的

一个正交矩阵 Q Q Q满足下列条件：

它是一个方阵（即行数等于列数）
它的每一列都是单位向量，并且相互正交

正交基

一个向量组 { u 1 , u 2 , ... , u n } \{\mathbf{u}_1,\mathbf{u}2,\ldots,\mathbf{u}n\} {u1,u2,...,un}是正交基，**如果组内的任意两个向量都是正交的，即 u i ⋅ u j = 0 \mathbf{u}{i}\cdot\mathbf{u}{j}=0 ui⋅uj=0（对于所有 i ≠ j i\neq j i=j），如果这些向量还都是单位向量，则称它们是正交规范基**

在三维空间中，标准基向量 { e 1 , e 2 , e 3 } \{\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3\} {e1,e2,e3}是一个正交规范基： e 1 = ( 1 , 0 , 0 ) , e 2 = ( 0 , 1 , 0 ) , e 3 = ( 0 , 0 , 1 ) \mathbf{e}_1=(1,0,0),\quad\mathbf{e}_2=(0,1,0),\quad\mathbf{e}_3=(0,0,1) e1=(1,0,0),e2=(0,1,0),e3=(0,0,1)

逆矩阵

假如说，矩阵 A A A是逆时针旋转90°的变换，则 A − 1 A^{-1} A−1是顺时针旋转90°的变换

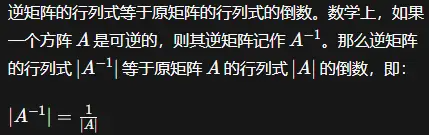
如果矩阵 A A A可逆，则 A − 1 = A ∗ ∣ ∣ A ∣ ∣ A^{-1}=\frac{A^{*}}{||A||} A−1=∣∣A∣∣A∗（ ∣ ∣ A ∣ ∣ = det ⁡ ( A ) ||A||=\det(A) ∣∣A∣∣=det(A)，即矩阵的行列式）

伴随矩阵

伴随矩阵 A ∗ A^{*} A∗

余子式：A A A关于第 i i i行第 j j j列的余子式（记作 M i j M_{ij} Mij）是去掉 A A A的第 i i i行第 j j j列之后得到的 ( n − 1 ) × ( n − 1 ) (n-1)\times (n-1) (n−1)×(n−1)矩阵的行列式

代数余子式：A A A关于第 i i i行第 j j j列的代数余子式（记作 C i j C_{ij} Cij）为 ( − 1 ) i + j M i j (-1)^{i+j}M_{ij} (−1)i+jMij

余子矩阵：A A A的余子矩阵是一个 n × n n\times n n×n的矩阵 C C C，使得第 i i i行第 j j j列的元素是 A A A关于第 i i i行第 j j j列的代数余子式

伴随矩阵：矩阵 A A A的伴随矩阵是 A A A的余子矩阵的转置矩阵

奇异值分解

特征分解只适用于方阵，奇异值分解SVD适用于任意矩阵分解

从相似对角化的的定义可以看到，我们可以把一个复杂的矩阵 A A A变成一个很简单的对角矩阵，而这个对角矩阵也同样保留了原来矩阵的特征，且变换的矩阵 P P P就是 A A A的特征向量组成的矩阵

但是注意，不是每一个矩阵都能与对角矩阵相似，首先注意到 P P P必须是可逆的，而 P P P又是特征向量组成 ⇒ \Rightarrow ⇒当且仅当 A A A有 n n n个线性无关的特征向量时， A A A才能相似对角化
奇异值分解就像是把一个复杂的玩具分解成几个更简单的小玩具，然后用这些小玩具重新拼装成原来的玩具

假设我们有一个 m × n m\times n m×n的矩阵 A A A，，奇异值分解把它分解成三个矩阵： A = U Σ V T A=U\Sigma V^{T} A=UΣVT

矩阵 U U U： m × m m\times m m×m的正交矩阵，其中的列向量 u 1 ⃗ , u 2 ⃗ , ... , u m ⃗ \vec{\mathrm{u}_1},\vec{\mathrm{u}_2},\ldots,\vec{\mathrm{u}_m} u1 ,u2 ,...,um 是 A A T AA^T AAT的特征向量，称为矩阵 A A A的左奇异向量
矩阵数学 Σ \Sigma Σ： m × n m\times n m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的元素 σ i \sigma_i σi称为奇异值， σ i = λ i \sigma_{\mathrm{i}}=\sqrt{\lambda_{\mathrm{i}}} σi=λi ， λ i \lambda_i λi是 A A T AA^T AAT的特征值
矩阵 V T V^T VT： n × n n\times n n×n的正交矩阵，其中的列向量 v ⃗ 1 , v ⃗ 2 , ... , v ⃗ m \vec{\mathrm{v}}{1} , \vec{\mathrm{v}}{2} ,\ldots, \vec{\mathrm{v}}_{\mathrm{m}} v 1,v 2,...,v m是 A T A A^TA ATA的特征向量，称为矩阵 A A A的右奇异向量

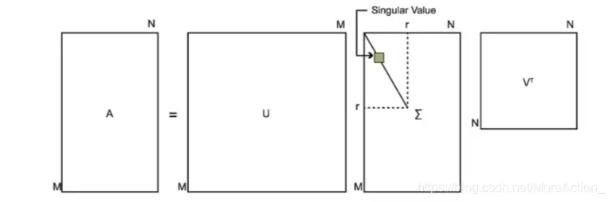
奇异值在矩阵中是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例 。也就是说，我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说： A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T \mathrm A_{\mathrm m\times\mathrm n}=\mathrm U_{\mathrm m\times\mathrm m}\Sigma_{\mathrm m\times\mathrm n}\mathrm V_{\mathrm n\times\mathrm n}^{\mathrm T}\approx\mathrm U_{\mathrm m\times\mathrm k}\Sigma_{\mathrm k\times\mathrm k}\mathrm V_{\mathrm k\times\mathrm n}^{\mathrm T} Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT，其中，k是一个远小于m、n的数。SVD具有的这种特性可以用于PCA降维、数据压缩和去噪等

A A T AA^T AAT是对称矩阵

主成分分析

假设我们有一组二维数据 ( x , y ) (x,y) (x,y)，它的分布如下：

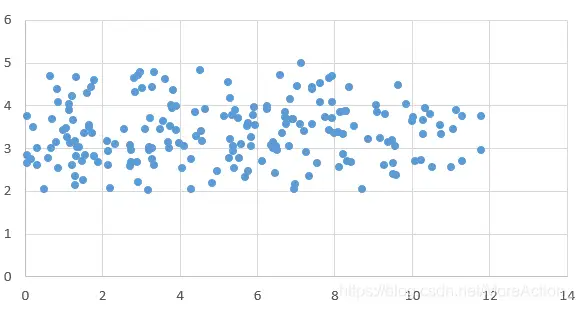
可以看到，数据在x轴上的变化大，而在y轴变化小，变化小意味着数据在这个特征上没有太大的差异，因此它包含的信息就比较少，那么我们就可以认为它是不重要的或者是噪音，从而可以直接将这个维度上的数据舍去，只用x轴上的数据来代替

那么假如数据是这样分布的呢？

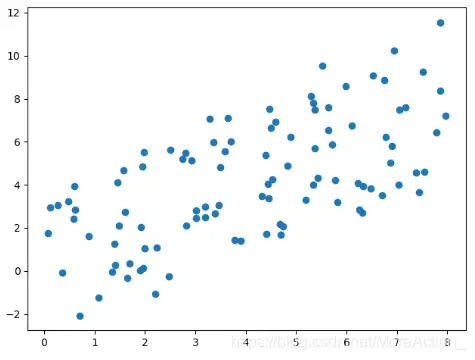
这个图我们就不太好看出到底是谁比较重要了，因为x和y变化都比较大，那么就不能降维了吗？非也，假如我们旋转一下坐标系

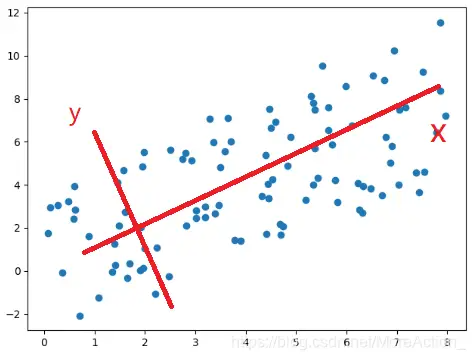
从这个例子也可以看到，数据本身的具体数值其实是不重要的，重要的是数据之间的关系，数据的整体分布。原来的数据是在 E E E坐标系下，然后我们换了一个坐标系来表示，本质上相当于对数据进行了一次正交变换（从数学公式看），在新的坐标系下，我们能更清楚的看到数据的特点
PCA的目标是将原始数据转换到一个新的坐标系中，这个新坐标系的轴（主成分）是数据方差最大的方向
主成分是在数据集中找到方差最大的方向（即主成分），然后将数据投影到这些方向上

方差最大化：每个主成分方向上数据的方差最大，这意味着这个方向上数据分布最广，包含最多的信息

正交性：不同主成分之间是相互正交的，即它们彼此垂直且不相关

PCA的步骤：

数据标准化：将每个特征的均值变为零，方差变为一，确保每个特征对主成分的贡献是均衡的 ⇒ \Rightarrow ⇒ 标准化数据 = X − μ σ \text{标准化数据}=\frac{X-\mu}\sigma 标准化数据=σX−μ
计算协方差矩阵：协方差矩阵描述了不同特征之间的线性关系 ⇒ \Rightarrow ⇒ Σ = 1 n − 1 X T X \Sigma=\frac{1}{n-1}X^TX Σ=n−11XTX，其中， Σ \Sigma Σ是协方差矩阵， X X X是标准化后的数据矩阵， n n n是样本数量
特征值分解：对协方差矩阵进行特征值分解，得到特征值和特征向量 ⇒ \Rightarrow ⇒ Σ = V Λ V T \Sigma=V\Lambda V^{T} Σ=VΛVT，其中， V V V是特征向量矩阵， Λ \Lambda Λ是对角矩阵，对角线上的元素是特征值
选择前 k k k个主成分：选择特征值最大的 k k k个特征向量，作为新的特征子空间的基，这些特征向量就是主成分；特征值代表了每个特征向量方向上的方差大小，特征值越大，表示这个方向上的方差越大，包含的信息越多
变换数据：用选择的 k k k个主成分对原始数据进行变换，得到降维后的数据 Y = X P Y=XP Y=XP，其中， Y Y Y是降维后的数据矩阵， P P P是由选择的 k k k个特征向量构成的矩阵

参考文献

1、ChatGPT3.5、ChatGPT4.0、ChatGPT4o

2、概率分布介绍---泊松分布：https://blog.csdn.net/weixin_44633882/article/details/120313676

3、相关系数------皮尔逊相关系数：https://blog.csdn.net/MoreAction_/article/details/106195689

4、《线性代数》教学视频宋浩老师：https://www.bilibili.com/video/BV1aW411Q7x1?p=1\&vd_source=8469f059ce75462e1674032ec0bfc23a

5、一文读懂特征值分解EVD与奇异值分解SVD：https://blog.csdn.net/MoreAction_/article/details/107318158

6、一文让你彻底搞懂主成成分分析PCA的原理及代码实现：https://blog.csdn.net/MoreAction_/article/details/107463336