通俗易懂讲解马尔可夫模型

本文旨在用通俗易懂的话介绍马尔可夫模型，为后面求解HMM（隐马尔可夫模型）做铺垫。需要的前置知识只有条件概率。

晴天 or 下雨？

首先思考一个问题，如果我想知道明天是否下雨，需要了解哪些信息呢？

假设我们只关注 "晴天" 和 "下雨" 两种天气：

如果今天是晴天，明天有 80% 概率继续晴天，20% 概率下雨；
如果今天是下雨，明天有 30% 概率转晴天，70% 概率继续下雨。

也就是说，在我们的这个模型中，明天是否下雨，仅依赖于今天的状态，而与过去无关。符合这种要求的模型，我们称为之马尔可夫模型。一句话总结就是：未来的状态，只和 "现在" 有关，和 "过去" 没关系。

如何定义"现在"

上面的这个模型，一般称为之一阶马尔可夫模型。也许大家会有疑问，实际生活中，昨天是否下雨也可能对明天产生影响啊？那不就是和过去有关系，不符合马尔可夫模型的定义了？为了回答这个问题，我们需要对"现在"这个词加深一下理解，马尔可夫链里的 "现在状态"，其实是个灵活的 "打包概念"，不是狭义的 "当前这一时刻的单一状态"。

我们可以把所有能影响明天天气的统称为现在，假设最近一个星期、甚至最近一年的天气，都对明天的天气有影响，那我们就把最近一个星期、最近一年统称为现在。只不过这个马尔可夫模型相比于之前多了非常多状态，也就变成了高阶马尔可夫模型（如果只考虑昨天、今天，就是二阶马尔可夫模型；如果只考虑前天、昨天、今天，就是三阶马尔可夫模型）

马尔可夫链里的 "现在"，不是忽略历史，而是把 "需要考虑的历史信息" 都装进 "当前状态" 这个 "包裹" 里------ 包裹里的信息越多，状态数越多，模型越复杂，但也能拟合更贴近现实的依赖关系。当然这就需要在模型复杂度和拟合效果上进行取舍了。

下面是一个马尔科夫模型在天气预测方面的简单例子

如果第一天是雨天，第二天还是雨天的概率是0.7，是晴天的概率是0.3；如果第一天是晴天，第二天还是晴天的概率是0.8，是雨天的概率是0.2。问：如果第一天下雨了，第二天仍然是雨天的概率是多少？，第十天是晴天的概率是多少？；经过很长一段时间后雨天、晴天的概率分别是多少？

首先我们需要定义状态为「雨天（R）」和「晴天（S）」

转移矩阵 P（行 = 当前状态，列 = 下一状态）为：

第一行表示今天下雨，明天下雨/晴天的概率分别为0.7/0.3

第二行表示今天晴天，明天下雨/晴天的概率分别为0.2/0.8

1. 第一天下雨，第二天仍为雨天的概率

问题中已直接给出：0.7。

2. 第一天下雨，第十天是晴天的概率

需通过 "状态向量 × 转移矩阵的幂次" 计算（第 1 天到第 10 天需转移 9 次）：

初始状态向量（第 1 天）：（1 = 雨天概率，0 = 晴天概率）
第 n 天的状态向量：

通过逐步递推（以状态向量中第二个元素为晴天概率）：

第 2 天：（晴天概率 0.3）
第 3 天：
第 4 天：
...
第 10 天：

因此，第十天是晴天的概率约为 0.599。

3. 长期后的稳态概率

当时间足够长，状态概率会进入 "平稳分布"，满足（状态不再变化），结合，列方程：

解第一个方程：，代入和为 1：

因此，长期后雨天概率为 0.4，晴天概率为 0.6。

结论

可以证明的是，满足以下三个条件的遍历马尔可夫链 （Ergodic Markov Chain），长期状态分布与初始状态无关：

不可约：任意两个状态之间可以 "互相到达"（比如天气模型中，雨天能转晴天，晴天也能转雨天）；
非周期：状态的 "周期" 为 1（比如雨天可以连续出现，不需要固定间隔才能出现）；
正常返：从任意状态出发，能以正概率回到该状态，且平均返回时间有限。

不过本人不是数学系的，这个证明过程就不在此班门弄斧了。在深度学习中，**绝大多数核心场景都会刻意设计或假设其为遍历马尔可夫链。**因此大家只需要知道这个结论，并不需要过度深入问题。

应用

马尔科夫模型未来状态只依赖当前状态、能通过转移概率建模规律的性质，在计算机领域有非常多的应用。它告诉我们不用纠结复杂的历史，只要抓住 "当前→下一步" 的关系，就能解决很多实际问题。

例如，用输入法打字时，输入 "今"，它自动联想 "天""晚""年"；AI 写短句时，"春风" 后面跟着 "拂面"，这些都靠马尔可夫链。刷短视频、逛购物 APP 时，系统把 "用户的行为" 当成 "状态"（比如 "看了美食视频""买了运动鞋""收藏了绘本"），马尔可夫链会统计 "状态转移概率"------ 比如 "看了汉堡视频后，再看薯条视频" 的概率是 60%，"买了篮球后，再买篮球袜" 的概率是 75%。刚刷到 "猫咪拆家" 的视频，系统就推 "猫咪玩具""宠物围栏"，就是因为它知道这两个行为的转移概率高。

代码

下面用python实现一个高阶马尔可夫链的简单数字序列预测

python 复制代码

import random
from collections import defaultdict

class HighOrderMarkovChain:
    def __init__(self, order=2):
        """
        初始化高阶马尔可夫链
        :param order: 马尔可夫链的阶数（比如2表示基于前2个状态预测下一个）
        """
        self.order = order  # 阶数
        # 转移概率字典：key=(前n个数字), value={下一个数字: 出现次数}
        self.transition_counts = defaultdict(lambda: defaultdict(int))

    def train(self, sequence):
        """
        训练模型：统计高阶状态的转移次数
        :param sequence: 训练用的数字序列（列表形式）
        """
        # 序列长度需大于阶数，否则无法训练
        if len(sequence) <= self.order:
            raise ValueError(f"训练序列长度必须大于阶数{self.order}")
        
        # 遍历序列，统计每个高阶状态的转移次数
        for i in range(len(sequence) - self.order):
            # 取前order个数字作为当前状态（元组可哈希，作为字典key）
            current_state = tuple(sequence[i:i+self.order])
            # 取下一个数字作为转移目标
            next_num = sequence[i+self.order]
            # 统计次数
            self.transition_counts[current_state][next_num] += 1

    def _get_next_num(self, current_state):
        """
        基于当前状态，按转移概率随机选择下一个数字（加权随机）
        :param current_state: 当前状态（元组，长度=order）
        :return: 预测的下一个数字
        """
        current_state = tuple(current_state)
        # 如果当前状态从未见过，随机返回一个训练过的数字（兜底）
        if current_state not in self.transition_counts:
            all_next_nums = []
            for state in self.transition_counts:
                all_next_nums.extend(self.transition_counts[state].keys())
            return random.choice(all_next_nums) if all_next_nums else 0
        
        # 提取当前状态的转移次数
        next_nums_count = self.transition_counts[current_state]
        # 计算总次数（用于算概率）
        total = sum(next_nums_count.values())
        # 按次数加权随机选择（次数越多，概率越高）
        rand_num = random.randint(1, total)
        cumulative = 0
        for next_num, count in next_nums_count.items():
            cumulative += count
            if cumulative >= rand_num:
                return next_num
        return 0  # 兜底

    def predict(self, initial_sequence, predict_length=5):
        """
        预测后续数字
        :param initial_sequence: 初始序列（列表，长度=order）
        :param predict_length: 要预测的数字个数
        :return: 完整序列（初始序列+预测序列）
        """
        if len(initial_sequence) != self.order:
            raise ValueError(f"初始序列长度必须等于阶数{self.order}")
        
        # 复制初始序列，避免修改原数据
        result = initial_sequence.copy()
        # 逐次预测下一个数字
        for _ in range(predict_length):
            # 取最后order个数字作为当前状态
            current_state = result[-self.order:]
            # 预测下一个数字
            next_num = self._get_next_num(current_state)
            # 添加到结果中
            result.append(next_num)
        return result

# ---------------------- 测试代码 ----------------------
if __name__ == "__main__":
    # 1. 准备训练数据（模拟的数字序列，可替换成任意自己的序列）
    # 比如：模拟"0,1,2"循环+少量随机的序列
    train_sequence = [0,1,2,0,1,2,0,1,2,0,1,3,0,1,2,0,1,2,1,2,3,1,2,3]
    print(f"训练序列：{train_sequence}")
    
    # 2. 初始化并训练二阶马尔可夫链
    markov = HighOrderMarkovChain(order=2)
    markov.train(train_sequence)
    
    # 3. 输入初始序列（长度=2），预测后续5个数字
    initial_seq = [0,1]  # 初始状态：前2个数字是0、1
    predict_seq = markov.predict(initial_seq, predict_length=5)
    
    # 4. 输出结果
    print(f"初始序列：{initial_seq}")
    print(f"预测后完整序列：{predict_seq}")
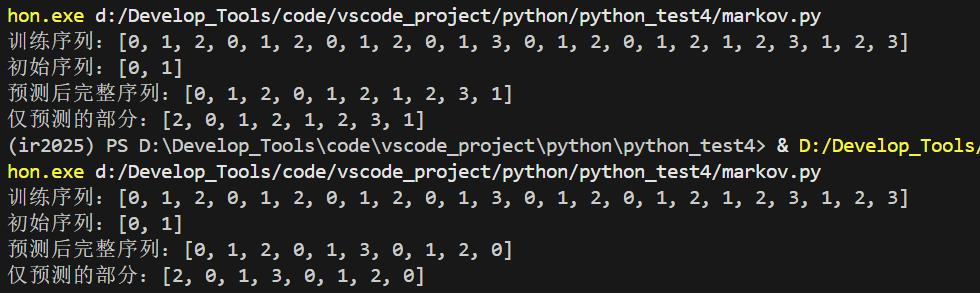
    print(f"仅预测的部分：{predict_seq[len(initial_seq):]}")

运行结果（预测后续5个/8个）