哈希
HashMap的含义比较晕,可以重做
双指针
双指针的起始位置和移动条件没转过来,可以重做
不太熟练,可以再做一遍
还可以用dp和单调栈做
双指针法:
首先需要注意的就是一个规律,从左到右,最大高度逐渐递增leftMax,从右到左,最大高度逐渐递增rightMax。
| height | 0 | 1 | 0 | 2 | 1 | 0 | 1 | 3 | 2 | 1 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| leftMax | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 |
| rightMax | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 1 | 0 |
所以每次比较的时候只需要比较leftMax和rightMax。
比如当遍历到下标2时,leftMax=1,虽然暂时不知道右边墙多高,但是右边的墙肯定大于等于现在的rightMax,所以只要leftMax<rightMax,这个地方就可以存水,高度为height[left],水量为leftMax-height[left]。
滑动窗口
这题HashMap超时
可以用数组存字母及其数量,使用Arrays.equals(a, b)进行对数组对比
子串
不可以根据当前窗口是否大于target就移动,因为有负数
创建前缀和pre,HashMap的key存前缀和,value存该前缀和的出现的次数
重点:
pre[i] = pre[i-1] + nums[i]
i~j符合条件:pre[i] = pre[j-1] + k 即 pre[j-1] = pre[i] - k
所以计数条件是map.containsKey(pre - k),证明有一个符合,cnt++
注意:
map.put(0, 1)初始化,因为前缀pre=k也算一个
return cnt;
用队列解决,保证队首是最大值,保证队第二位往后越来越小,如果大于队尾就把队尾弹出
让下标入队,便于检测是否离开滑动窗口
做的有点磕磕绊绊,容易超时,注意hashmap的使用
普通数组
二维数组排序用Arrays.sort
注意最后一次start和end的处理
一个区间的数组单独处理
list.toArray可以把list转化为数组
注意k>nums.length的处理
可以用逆序数组操作得到
除了可以用Arrays.sort之外还有一个方法
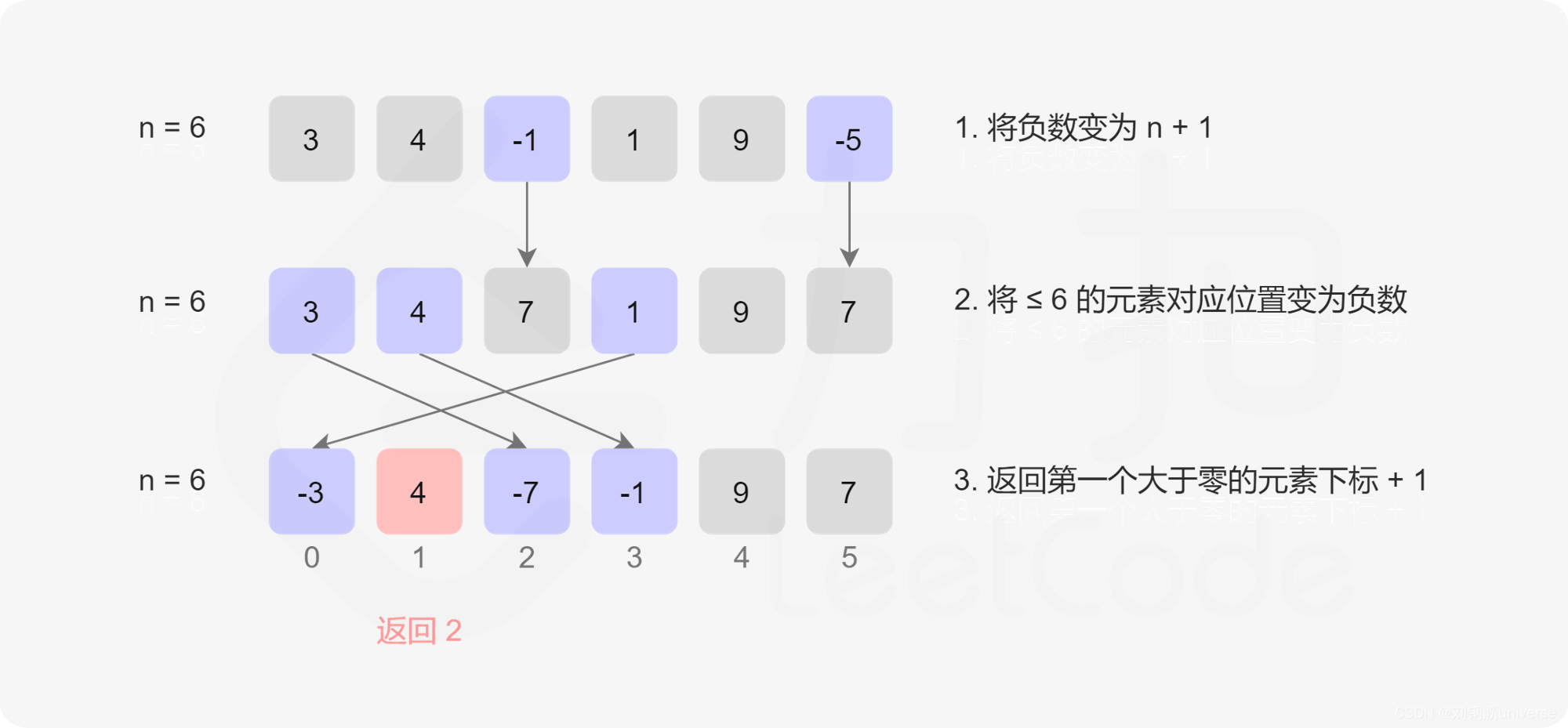
缺失的正数一定在[1, nums.length]之间
第一轮循环,先把负数和0变成nums.length+1,打标记
第二轮循环,选择值x为1~nums.length之间的,将此数作为下标,将nums[x-1]变成负的,打标记
第三轮循环,选择第一个值大于0的,返回其下标index+1
太巧妙了
矩阵
做的老费劲了,还好做出来了
用一个变量存数,完成一圈四个数字的转换
有个坑
不要沿着对角线判断,因为下一行的第一个可能比上一行的最后一个小,比如
{1, 10}
{2, 11}
{3, 12}
{4, 13}
可以对每一行使用二分查找
链表
注意交叉点不是快慢指针相遇的点,是相遇点指针和头节点指针共同前进相遇的点
可以用map来解决,键是原list的节点,值是新list的节点,只有map里没有原node对应的新node时,创建新节点,把新节点加入map,并递归创建next和random,最后将创建的新节点返回,完成当前节点的赋值。
给链表排序,比较难,可以重做。
对链表自顶向下归并排序
- 找到链表的中点,以中点为分界,将链表拆分成两个子链表。寻找链表的中点可以使用快慢指针的做法,快指针每次移动2步,慢指针每次移动1步,当快指针到达链表末尾时,慢指针指向的链表节点即为链表的中点。
- 对两个子链表分别排序。
- 将两个排序后的子链表合并,得到完整的排序后的链表。
可以使用递归的方式,拆分排序作为一个方法递归,调用合并方法进行合并。
创建一个新类,可以用双向链表记录缓存key和value,然后用HashMap提供key和node的对应关系,设置头尾节点方便对首尾进行操作。
二叉树
需要先交换左右节点,然后再递归左右,不能直接交换左子树和右子树
可以用队列辅助求解,每次进对应该相等的节点
最长的也就是两条最深的路径相加,路径长=经过的节点-1,可以利用求深度的函数,每次更新ans为左右深度相加最大值。
注意:二叉搜索树中序是递增有序序列
记得维护一个maxNode记录当前最大值,比较当前节点与当前最大值,必须当前更大才能继续,不然false
能想到中序遍历,但是递归不好做,要用迭代中序遍历
迭代:用栈模拟递归,中序进栈是左-中-右
有意思,可以重做
穷举,访问一个node节点,检测以node为起始节点往下延伸的路径有多少种,递归遍历每一个节点开始所有可能的路径,然后把路径相加。
定义新函数,计算以node为起始节点的符合要求的路径数
可以重做
后序遍历之后回溯
如果左右都搜到,返回root
左有右无,返回左,反之亦然,这里是这个节点是祖先但是不是最近,因此要返回给上层
左无右无,返回null
重做
这题有点复杂
可以创建一个方法计算最大子树和
返回值:node+node.left或node+node.right的最大值,作为结果路径的一部分
先计算left和right的方法返回值,注意返回值和0取最大值,负数直接不考虑
最大子树和全局变量二者取最大:左根右/原来的最大值
注意:maxSum作为全局变量计算,不需要用方法返回值,方法返回的是目前一条线的路径和
重做
回溯
这题有点绕
因为可以从任意一点开始
需要二维数组标记本次序列中的visited
结束条件:当前字母不匹配,false;当前是word最后一个字母且匹配,true;
其他情况再标记visited,不可以在之前就标记
可以用二维数组表示行动路线上下左右
二分查找
虽然前后颠倒,但是仍然可以用二分查找
mid左右两侧肯定有一边是有序的
所以分支可以按照以下判断:
nums[0] < nums[mid]:左侧有序,看target值和nums[mid]的大小
else:nums[mid] < nums[nums.length()-1]:右侧有序,看target值和nums[mid]的大小
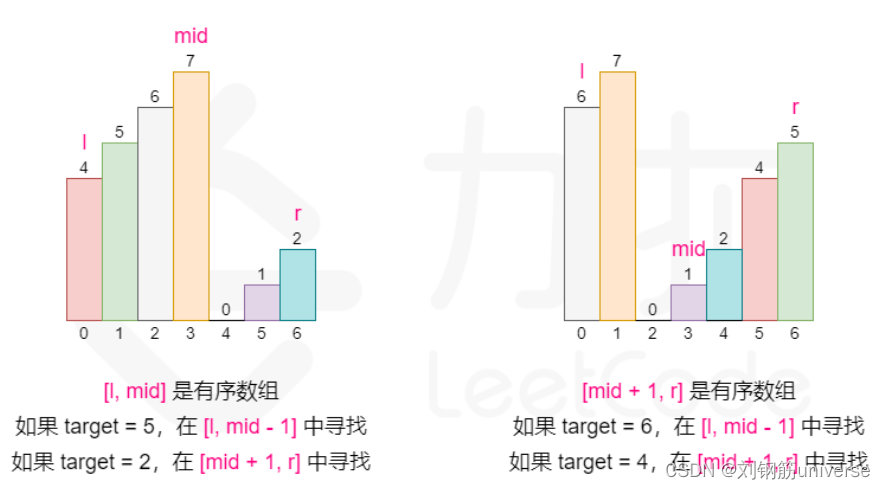
153.寻找旋转排序数组中的最小值
注意结束条件:区间长度为1,且不存在mid和high位置的数字相等的情况
如果右侧有序:移动high到mid
else:low = mid + 1
贪心
增加步数的时机:当前再跳就到末尾;当前位置为当前覆盖的最大区域
更新当前范围的时机:走到当前区域的最后一个位置
更新最大范围的时机:每一次循环都更新最大范围
解题方式比较有意思,可以用数组记录字母的最后出现时间,检查当前是不是已经到maxIndex,不算严格的贪心
动态规划
完全背包问题
背包:n;物品:每个组成完全平方的数
可以重做
可以先遍历硬币种类,再遍历数值,递推公式:dp[j] = Math.min(dp[j-coins[i]]+1, dp[j])
用set装list里的单词,用i和j表示子串的起始位置
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);(j在0~i的循环中)
这题不能用之前的根据前一个的乘积推,因为如果两个负数相乘就会变成正数
可以理解为记录最大数和最小数,递推公式:
java
maxF[i] = Math.max(maxF[i-1]*nums[i], Math.max(nums[i], minF[i-1] * nums[i]));
minF[i] = Math.min(minF[i-1]*nums[i], Math.min(nums[i], maxF[i-1] * nums[i]));minF[i-1] * nums[i]最大的情况是(-5)(-2)这种
maxF[i-1] * nums[i]最大的情况是5(-2)这种
01背包问题
- 如果本字符是),前一个是(,那么可以是dp[i-1]+2
- 如果本字符是),前一个不是(,i-dp[i-1]-1是(,那么可以是dp[i-1]+dp[i-dp[i-1]-2]+2,前者代表前一位的连续长度,后者代表前一段再往前如果对应,那么加上前面的连续长度,例如()((())),dp[6]=4,发现第7位减掉前面连续的4之后对应的是(,可以在此基础上加2,再加上前面的dp[1]的连续长度
可以这样理解:
先遍历子串长度,再遍历起始位置,根据子串长度和起始位置得到终止位置,判断双端是否相等
dp可以表示这一段是否是回文,用maxLen记录最长长度
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]
重做
栈
单调栈的经典题目
找低-高-低进行计算
可以重做
技巧
可以使用以下思路:
- 设置变量i为len-2,jk为len-1
- 从后往前找一个相邻升序的元素对,满足Ai<Aj,此时j到end肯定是降序
- 在j到end从后向前找一个满足Ai<Ak的k
- 将Ai与Ak交换
- 这时候j到end肯定是降序,逆序j到end让它升序
- 如果2中找不到相邻元素对,证明现在整个序列都是降序,那就直接跳到4
图
其实是dfs拓扑排序,如果有环则false
可以设置节点的不同状态:正在访问、已访问、未访问
从未访问节点开始dfs,如果发现该点的对应节点也是正在访问,则false
需要注意:如果List<List<>>已经初始化内部ArrayList,就算是空的,get也不会报错。
ArrayList中,add方法不会覆盖原值,而是将新值添加到列表的末尾。因此,调用edges.get(edge[1]).add(edge[0]);不会覆盖任何已有的值,而是将edge[0]追加到edges.get(edge[1])返回的列表的末尾。
这和图有什么关系
这题前缀树可以理解为字符串前缀每一个字符都占一层,Trie[] children; // 指向子节点的指针数组,boolean isEnd; // 是不是字符串的结尾
孩子children[0]表示a,然后进行查找插入等操作
堆
快排超时
使用堆排序
需要注意:
建堆 的过程和堆排序过程类似,建堆从1/2节点处逆序开始,1/2即最后一个父节点,比较父子节点是否需要交换。
堆排序 的过程需要先交换堆顶即0和最后未排序的数字,然后对剩余未排序数组进行排序。
重做
可以用堆和优先队列,用hashmap统计出现次数后,遍历hashmap,如果队列未满入队
如果队列已满,比较队首元素,如果当前count更多就弹出加入当前count
java
PriorityQueue<int[]> queue = new PriorityQueue<int[]>((o1, o2) -> o1[1]-o2[1]);是小顶堆,按照升序排序,每次出队的是最小值
由于是数据流,考虑变动的情况
可以设置两个优先队列分别表示小于中位数和大于中位数的情况
保证两个队列大小相等或一方大1位数
小于中位数的队列队首为最大值,大于中位数的队列队首为最小值
完结撒花***