目录
蒙特卡洛方法
第二节 推导贝尔曼最优公式中的:
q π k ( s , a ) = ∑ r P ( r ∣ s , a ) r + γ ∑ s ′ P ( s ′ ∣ s , a ) v π k ( s ′ ) q_{\pi_k}(s,a) = \sum_{r} P(r|s,a)r + \gamma \sum_{s'} P(s'|s,a) v_{\pi_k}(s') qπk(s,a)=r∑P(r∣s,a)r+γs′∑P(s′∣s,a)vπk(s′)
时提到过,其中的 P ( r ∣ s , a ) , P ( s ′ ∣ s , a ) P(r|s,a), P(s'|s,a) P(r∣s,a),P(s′∣s,a) 都认为是已知的,这种也被称为 model-based 强化学习。而这一节中,我们要考虑 model-free 的强化学习形式。此时 P ( r ∣ s , a ) , P ( s ′ ∣ s , a ) P(r|s,a), P(s'|s,a) P(r∣s,a),P(s′∣s,a) 不再是已知的,那么为了"估计"这些信息,我们需要使用到蒙特卡洛方法。简单来说,就是 通过大量的模拟实验,用大量的实验的结果来估测模型参数,蒙特卡洛方法的可行性由 大数定律 保证:
对一个随机变量 X X X,假设 { x i } \{x_i\} {xi} 是独立同分布的样本,记 x ˉ = 1 n ∑ i n x i \bar{x} = \frac{1}{n} \sum_{i}^n x_i xˉ=n1∑inxi,则:
E ( x ˉ ) = E [ X ] v a r [ x ˉ ] = 1 n v a r [ X ] \begin{aligned}E(\bar{x}) &= E[X]\\ var[ \bar{x}] &= \frac{1}{n} var[X]\end{aligned} E(xˉ)var[xˉ]=E[X]=n1var[X]因此 x ˉ \bar{x} xˉ 是 E [ X ] E[X] E[X] 的无偏估计,且由于 lim n → ∞ v a r [ x ˉ ] = 0 \lim_{n \rightarrow \infin} var[ \bar{x}] = 0 limn→∞var[xˉ]=0,因此当 n 足够大, x ˉ \bar{x} xˉ 趋于 E [ X ] E[X] E[X]
事实上,用蒙特卡洛方法来估计 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a),用其原始的定义更易理解和使用:
q π k ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_{\pi_k}(s,a) = E[G_t | S_t =s, A_t =a] qπk(s,a)=E[Gt∣St=s,At=a]
MC Basic算法
回忆 第二节 中策略迭代的步骤:
已知 π k → ( v π k ( 0 ) → v π k ( 1 ) → . . . → v π k ( ∞ ) = v π k ) → 求解 q π k ( s , a ) → π k + 1 = { 1 , a = a ∗ ( s ) 0 , a ≠ a ∗ ( s ) → . . . 已知 \pi_k \rightarrow (v_{\pi_k}^{(0)} \rightarrow v_{\pi_k}^{(1)} \rightarrow ... \rightarrow v_{\pi_k}^{(\infin)} = v_{\pi_k}) \rightarrow 求解 q_{\pi_k}(s,a) \rightarrow \pi_{k+1}= \begin{cases} 1, \quad a = a^*(s)\\ 0, \quad a \neq a^*(s) \end{cases} \rightarrow ... 已知πk→(vπk(0)→vπk(1)→...→vπk(∞)=vπk)→求解qπk(s,a)→πk+1={1,a=a∗(s)0,a=a∗(s)→...
上面跟值迭代相比最主要的不同是 ( v π k ( 0 ) → v π k ( 1 ) → . . . → v π k ( ∞ ) = v π k ) (v_{\pi_k}^{(0)} \rightarrow v_{\pi_k}^{(1)} \rightarrow ... \rightarrow v_{\pi_k}^{(\infin)} = v_{\pi_k}) (vπk(0)→vπk(1)→...→vπk(∞)=vπk),将其展开:
v π k ( 1 ) = r π k + γ P π k v π k ( 0 ) v π k ( 2 ) = r π k + γ P π k v π k ( 1 ) ... v π k ( ∞ ) = r π k + γ P π k v π k ( ∞ ) \begin{aligned} v_{\pi_k}^{(1)} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(0)}\\ v_{\pi_k}^{(2)} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(1)}\\ & \dots \\ v_{\pi_k}^{(\infin)} &= r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(\infin)}\\ \end{aligned} vπk(1)vπk(2)vπk(∞)=rπk+γPπkvπk(0)=rπk+γPπkvπk(1)...=rπk+γPπkvπk(∞)
这里由于 P ( r ∣ s , a ) , P ( s ′ ∣ s , a ) P(r|s,a), P(s'|s,a) P(r∣s,a),P(s′∣s,a) 未知,我们 不再通过迭代的方式求解 v π k v_{\pi_k} vπk,再来求解 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) 了,而是直接根据一些 experiment (即样本) 来估计 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) ,上述算法变成:
已知 π k → 从 ( s , a ) 出发,做 n 次实验,有 n 个结果 g π k ( i ) ( s , a ) → 估计 q π k ( s , a ) = 1 n ∑ i g π k ( i ) ( s , a ) → π k + 1 = { 1 , a = a π k ( s ) 0 , a ≠ a π k ( s ) → . . . 已知 \pi_k \rightarrow 从 (s,a) 出发,做n次实验,有n个结果 g_{\pi_k}^{(i)}(s,a) \rightarrow 估计 q_{\pi_k}(s,a) = \frac{1}{n}\sum_i g_{\pi_k}^{(i)}(s,a) \rightarrow \pi_{k+1}= \begin{cases} 1, \quad a = a_{\pi_k}(s)\\ 0, \quad a \neq a_{\pi_k}(s) \end{cases} \rightarrow ... 已知πk→从(s,a)出发,做n次实验,有n个结果gπk(i)(s,a)→估计qπk(s,a)=n1i∑gπk(i)(s,a)→πk+1={1,a=aπk(s)0,a=aπk(s)→...
其中 a π k ( s ) = arg max a ∈ A q π k ( s , a ) a_{\pi_k}(s) = \argmax_{a \in A} q_{\pi_k}(s,a) aπk(s)=a∈Aargmaxqπk(s,a)
下面可以看一些例子:
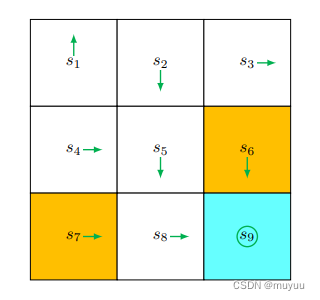
对于上图这样一个 grid-world 而言,一共有9个 state,每个 state 都有五种 action,假设对于每个 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) 需要找 n n n 个样本来做估计,那么一共需要 45 ∗ n 45*n 45∗n 个样本。下面我们仅以 s 1 s_1 s1 为例来拆解一下:
由于上述 grid-world 是确定形式的,因此每个 ( s , a ) (s,a) (s,a) 实际不论采多少次样,结果都是相同的,即 g π k ( i ) ( s , a ) , i = 1 , 2 , 3... g_{\pi_k}^{(i)}(s,a), i = 1,2,3... gπk(i)(s,a),i=1,2,3... 都相同。(对于概率形式的 policy 而言,就可以进行大量不同的采样)
- 对 ( s 1 , a 1 ) (s_1, a_1) (s1,a1),路径总为 s 1 → a 1 s 1 → a 1 s 1 → a 1 . . . s_1 \overset{a_1} \rightarrow s_1 \overset{a_1} \rightarrow s_1 \overset{a_1} \rightarrow ... s1→a1s1→a1s1→a1...: q π 0 ( s 1 , a 1 ) = − 1 + γ ( − 1 ) + γ 2 ( − 1 ) + . . . = − 1 1 − γ q_{\pi_0}(s_1, a_1) = -1 + \gamma (-1) + \gamma^2 (-1) + ... = \frac{-1}{1-\gamma} qπ0(s1,a1)=−1+γ(−1)+γ2(−1)+...=1−γ−1
- 对 ( s 1 , a 2 ) (s_1, a_2) (s1,a2),路径总为 s 1 → a 2 s 2 → a 3 s 5 → a 3 . . . s_1 \overset{a_2} \rightarrow s_2 \overset{a_3} \rightarrow s_5 \overset{a_3} \rightarrow ... s1→a2s2→a3s5→a3...: q π 0 ( s 1 , a 2 ) = 0 + γ ( 0 ) + γ 2 ( 0 ) + γ 3 ( 1 ) + γ 4 ( 1 ) + . . . = γ 3 1 − γ q_{\pi_0}(s_1, a_2) = 0 + \gamma (0) + \gamma^2 (0) + \gamma^3 (1) + \gamma^4 (1) + ... = \frac{\gamma^3}{1-\gamma} qπ0(s1,a2)=0+γ(0)+γ2(0)+γ3(1)+γ4(1)+...=1−γγ3
- 对 ( s 1 , a 3 ) (s_1, a_3) (s1,a3),路径总为 s 1 → a 3 s 4 → a 2 s 5 → a 3 . . . s_1 \overset{a_3} \rightarrow s_4 \overset{a_2} \rightarrow s_5 \overset{a_3} \rightarrow ... s1→a3s4→a2s5→a3...: q π 0 ( s 1 , a 2 ) = 0 + γ ( 0 ) + γ 2 ( 0 ) + γ 3 ( 1 ) + γ 4 ( 1 ) + . . . = γ 3 1 − γ q_{\pi_0}(s_1, a_2) = 0 + \gamma (0) + \gamma^2 (0) + \gamma^3 (1) + \gamma^4 (1) + ... = \frac{\gamma^3}{1-\gamma} qπ0(s1,a2)=0+γ(0)+γ2(0)+γ3(1)+γ4(1)+...=1−γγ3
- 对 ( s 1 , a 4 ) (s_1, a_4) (s1,a4),路径总为 s 1 → a 4 s 1 → a 1 s 1 → a 1 . . . s_1 \overset{a_4} \rightarrow s_1 \overset{a_1} \rightarrow s_1 \overset{a_1} \rightarrow ... s1→a4s1→a1s1→a1...: q π 0 ( s 1 , a 1 ) = − 1 + γ ( − 1 ) + γ 2 ( − 1 ) + . . . = − 1 1 − γ q_{\pi_0}(s_1, a_1) = -1 + \gamma (-1) + \gamma^2 (-1) + ... = \frac{-1}{1-\gamma} qπ0(s1,a1)=−1+γ(−1)+γ2(−1)+...=1−γ−1
- 对 ( s 1 , a 5 ) (s_1, a_5) (s1,a5),路径总为 s 1 → a 5 s 1 → a 1 s 1 → a 1 . . . s_1 \overset{a_5} \rightarrow s_1 \overset{a_1} \rightarrow s_1 \overset{a_1} \rightarrow ... s1→a5s1→a1s1→a1...: q π 0 ( s 1 , a 1 ) = 0 + γ ( − 1 ) + γ 2 ( − 1 ) + . . . = − γ 1 − γ q_{\pi_0}(s_1, a_1) = 0 + \gamma (-1) + \gamma^2 (-1) + ... = \frac{-\gamma}{1-\gamma} qπ0(s1,a1)=0+γ(−1)+γ2(−1)+...=1−γ−γ
因此 a π 0 ( s ) = arg max a ∈ A q π 0 ( s 1 , a ) = 2 或 3 a_{\pi_0}(s) = \argmax_{a \in A} q_{\pi_0}(s_1,a) = 2 \text{ 或 } 3 aπ0(s)=argmaxa∈Aqπ0(s1,a)=2 或 3。实时上我们也可直观看到,将 s 1 s_1 s1 处的 action 改成 a 2 a_2 a2 或者 a 3 a_3 a3 均可将 s 1 s_1 s1 处的 action 调整至最优。
NOTE: 上述例子中,是为了方便理解,所以相当于是把 model (即 P ( r ∣ s , a ) P(r|s,a) P(r∣s,a) 和 P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a) )都展示出来了,但实际的情况应该是:我们并不知道 model 是怎样的,但是从每个 ( s 1 , a i ) (s_1, a_i) (s1,ai) 出发采样 n n n 次,会发现每次采出来的 trajectory 都是相同的,然后我们依然按 q π 0 ( s 1 , a ) = 1 n ∑ i g π 0 ( i ) ( s 1 , a ) q_{\pi_0}(s_1,a) = \frac{1}{n}\sum_i g_{\pi_0}^{(i)}(s_1,a) qπ0(s1,a)=n1∑igπ0(i)(s1,a) 来估计 q π 0 ( s 1 , a ) q_{\pi_0}(s_1,a) qπ0(s1,a),其实就还是上述的结果。
另一个更有意思的例子是:
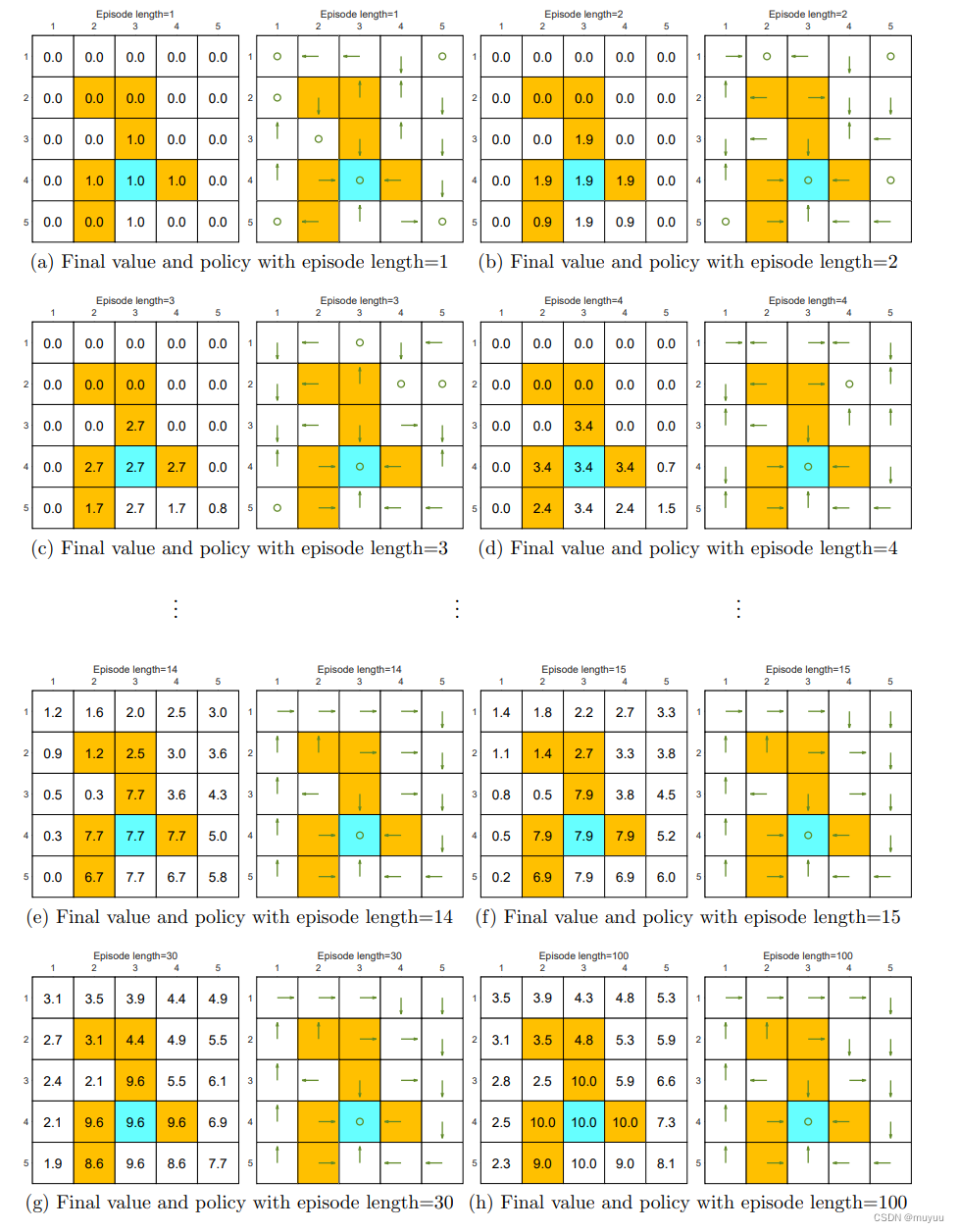
前一个例子,我们采样的 trajectory 是无限长的,但在这个例子中,我们将采样的 trajectory 的长度从1开始逐渐递增,然后可以观察到一个有趣的现象:当采样的 trajectory 的长度比较小时,只有更靠近 target state的 state,其 state value 才能算到为正,而更远的 state,其 state value 都为0。从公式上来说也很好理解,由于: v π ( s ) = ∑ a π ( a ∣ s ) q π ( s , a ) v_{\pi}(s) = \sum_a \pi(a|s) q_{\pi}(s,a) vπ(s)=a∑π(a∣s)qπ(s,a) ,因此贪婪policy下, v π ( s ) = max a q π ( s , a ) v_{\pi}(s) = \max_{a}q_{\pi}(s,a) vπ(s)=amaxqπ(s,a),而从上一个例子不难得知 q π ( s , a ) q_{\pi}(s,a) qπ(s,a) 要能走到 target state,才能开始拿到正的分数,因此如果 trajectory 的长度太短,以至于甚至走不到 target state,那么 q π ( s , a ) = 0 q_{\pi}(s,a) = 0 qπ(s,a)=0,因此 v π ( s ) v_{\pi}(s) vπ(s) 也为0。
sparse reward
上述现象也称为 sparse reward,因为其 reward 是稀疏的,即前面走对很多步都没有reward,必须到 target state 开始才有 reward。对于特别大的 state space 来说, sparse reward 会导致模型效率低下,因为每个样本的计算量都大大提升。有一些方法可以缓解这样的问题,例如:如果能走到离 target state 比较近的 state,那么也可以拿到一定的 reward,离得越近,reward 越大。更多可见 Reference
MC Greedy 算法
上述 MC Basic 方法在实际使用时,还有很多地方需要改进:
样本使用效率
以上面第一个例子为例:

当从 ( s 1 , a 2 ) (s_1, a_2) (s1,a2) 出发,其实计算其 action state 时,还同时可以算到很多后面的 state 的 action state :
s 1 → a 2 s 2 → a 4 s 1 → a 2 s 2 → a 3 s 5 → a 1 ⋯ [ ( s 1 , a 2 ) 的样本 ] s 2 → a 4 s 1 → a 2 s 2 → a 3 s 5 → a 1 ⋯ [ ( s 2 , a 4 ) 的样本 ] s 1 → a 2 s 2 → a 3 s 5 → a 1 ⋯ [ ( s 1 , a 2 ) 的样本 ] s 2 → a 3 s 5 → a 1 ⋯ [ ( s 2 , a 3 ) 的样本 ] s 5 → a 1 ⋯ [ ( s 5 , a 1 ) 的样本 ] \begin{aligned} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_4} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1}& \cdots \quad [(s_1, a_2)\text{ 的样本}]\\ \quad\\ s_2 \xrightarrow{a_4} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1}& \cdots \quad [(s_2, a_4)\text{ 的样本}]\\ \quad\\ s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1}& \cdots \quad [(s_1, a_2)\text{ 的样本}]\\ \quad\\ s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1}& \cdots \quad [(s_2, a_3)\text{ 的样本}]\\ \quad\\ s_5 \xrightarrow{a_1}& \cdots \quad [(s_5, a_1)\text{ 的样本}] \end{aligned} s1a2 s2a4 s1a2 s2a3 s5a1 s2a4 s1a2 s2a3 s5a1 s1a2 s2a3 s5a1 s2a3 s5a1 s5a1 ⋯[(s1,a2) 的样本]⋯[(s2,a4) 的样本]⋯[(s1,a2) 的样本]⋯[(s2,a3) 的样本]⋯[(s5,a1) 的样本]
因此我们会发现:可能不需要从每一个 state 出发,而只要从一些比较前面的 state 出发,就有可能给后面的 (state, action) 也得到足够多的样本。
顺便再介绍两个相关的概念,从上例也能发现,即使是同一条 trajectory ,也可能经过某对 (state, action) 好几次 (eg:上面的 ( s 1 , a 2 ) (s_1, a_2) (s1,a2)) :
- first-visit strategy:如果采样时,只采第一次出现的样本
- every-visit strategy:如果采样时,采全部出现的样本
MC ϵ \epsilon ϵ-Greedy 算法
上面我们已经探讨了 MC Basic 的一个改进方向,就是不用真的对每一个 (state, action) 进行遍历,而是可以选几个 state ,然后进行足够长的探索。那么问题来了:需要选怎样的 state,多长的 trajectory ,才能让每对 (state, action) 都采到足够的样本呢?
这里就来到了 exploration 和 exploitation 的balance :exploitation :很好理解,就是要选取最优的 Policy,而前面我们已经证明过,最优的 Policy 就是贪婪形式的: π k + 1 ( a ∣ s ) = { 1 , a = a k ∗ ( s ) 0 , a ≠ a k ∗ ( s ) \pi_{k+1}(a|s) = \begin{cases} 1, \quad a = a^*_k(s)\\ 0, \quad a \neq a^*_k(s) \end{cases} πk+1(a∣s)={1,a=ak∗(s)0,a=ak∗(s)
那既然能找到最优策略,又扯到 exploration 什么事呢?这是因为 a k ∗ ( s ) = arg max a ∈ A q π k ( s , a ) a^*k(s) = \argmax{a \in A} q_{\pi_k}(s,a) ak∗(s)=a∈Aargmaxqπk(s,a) 实际是求不到的。因为 第一节 就提到过: 为了一般性,我们后面讨论的都是 continuing task,将 target state 也看作普通的 state,可以离开,只是每次进入 target state 时 ,reward 加 1 。所以每个 q π k ( s , a ) q_{\pi_k}(s,a) qπk(s,a) 对应的都是一个无限长的 trajectory ,上例中可以把值求出来,是因为它刚好是一个收敛的级数,但不是所有的情况我们都保证 reward 级数可以收敛。这样就会导致一个问题:我们不能直接信任贪婪形式的结果。与此同时,贪婪形式带来的坏处是:它的每一条 trajectory 能覆盖的样本比较有限,所以需要的 trajectory 会比较多,计算量也比较大。既然反正都无法保证得到的策略是最优的,还不如为了更快得得到一个可用的策略,再保留一些探索性,因此提出了 MC ϵ \epsilon ϵ-Greedy 算法 :
π k + 1 ( a ∣ s ) = { 1 − ∣ A ∣ − 1 ∣ A ∣ ϵ , a = a k ∗ ( s ) 1 ∣ A ∣ ϵ , a ≠ a k ∗ ( s ) \pi_{k+1}(a|s) = \begin{cases} 1 - \frac{|A|-1}{|A|} \epsilon, \quad a = a^*_k(s)\\ \frac{1}{|A|} \epsilon, \quad a \neq a^*_k(s) \end{cases} πk+1(a∣s)={1−∣A∣∣A∣−1ϵ,a=ak∗(s)∣A∣1ϵ,a=ak∗(s)
其中 ∣ A ∣ |A| ∣A∣ 是 action 的种数。即对每个非最优的 action,仍然给一点点的概率,使得 trajectory 仍有可能往这个方向走。 (这里与深度学习中 "贪婪搜索会导致局部最优,所以用 beam search 来增大一些探索的空间" 形似而神不似 ,因为对于很多的序列学习任务,它的长度是 有限且已知 的,因此它的最优解是可以求到的,只是计算量过大实际不太可行。而这里的最优解,是理论都不可知的 (model-free 时,前面 model-based 的情况,理论上还是可以用贝尔曼最优公式求解的),增大搜索的目的是为了减少计算量,而 beam search 是为了得到更好的结果而增加计算量 )。以下是 exploration 和 exploitation 的balance 的总结:
- 大 ϵ \epsilon ϵ + 短&少的 trajectory,偏向于 exploration。样本量少,计算快,但找到的策略差
- 小 ϵ \epsilon ϵ + 长&多的 trajectory,偏向于 exploitation。样本量大,计算慢,但找到的策略更优
一些例子
还是看一些例子来加深理解:
- ϵ \epsilon ϵ 的影响
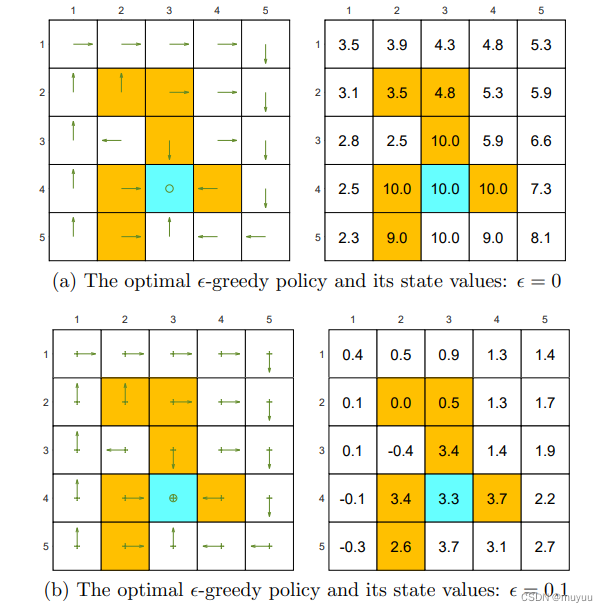
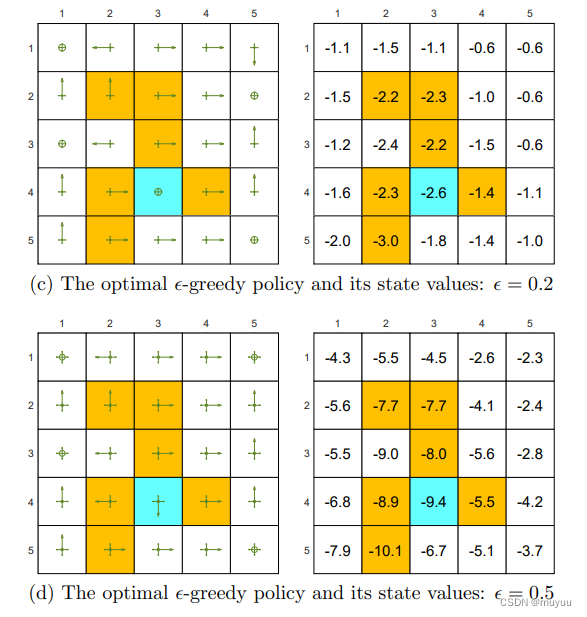
从 (a) 到 (d), ϵ \epsilon ϵ 从0开始逐渐增大,可以看到 state value 也在逐渐变小,说明策略在逐渐变"差",但 (b) 至少跟 (a) 还是 consistent 的,即最大概率的 action 和 (a) 还是相同,而 © 和 (d),甚至有的 state 最优 action 已经变了。这其中的原因,可以以 target value 为例讨论一下: 当 ϵ \epsilon ϵ 比较大时,从 target state 出发,往各个方向探索的概率都比较大了,但是 target value 周围大部分都是 forbidden state,因此总是会拿到负分,尽管我们希望的结果是:在 target state 学会呆在原地,但呆在原地就有比较大的几率拿负分,相反往下走出去了,反而不容易拿负分,因此它最后学到的是在 target state 要往下走出去。
- ϵ \epsilon ϵ 的大小与所需 trajectory 条数的关系
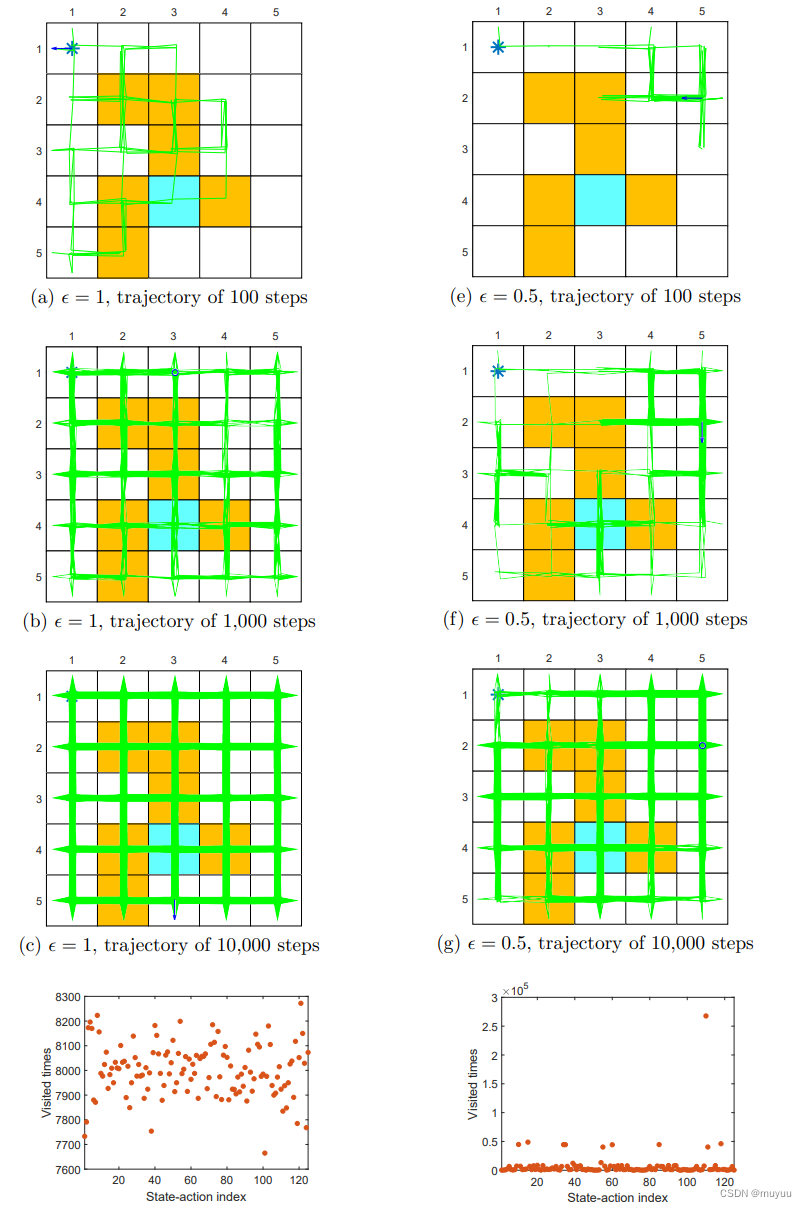
左边一列是 ϵ = 1 \epsilon =1 ϵ=1 时,表明各个方向探索的概率相等。右边一列是 ϵ = 0.5 \epsilon =0.5 ϵ=0.5 时,表明探索性弱一些。可以看到:
- ϵ \epsilon ϵ 较大时,同样长度的 trajectory 探索到的 (state,action) 种数更多,甚至长度较长时,一条 trajectory 就足以产生所有 (state,action) 的样本了
- ϵ \epsilon ϵ 较大时,一条 trajectory 产生的样本在不同 (state,action) 的分布也比较均匀,即采样比较均匀;而 ϵ \epsilon ϵ 较小时,会出现大部分 (state,action) 采样比较少,而个别 (state,action) 采样多得多的情况
结论: ϵ \epsilon ϵ 和 trajectory 的条数,均为MC ϵ \epsilon ϵ-Greedy 算法的超参数,需要根据实验来调整,更大的 ϵ \epsilon ϵ 可以减少马尔可夫模拟次数,但是得到的策略效果也会更差一些,而更小的 ϵ \epsilon ϵ 计算量更大,结果也更好。一般可以前期采用大的 ϵ \epsilon ϵ ,加大探索空间,快速找到一个差不多的策略,后期再改成小的 ϵ \epsilon ϵ ,找更好的策略。
Reference: