周志华《机器学习---西瓜书》二
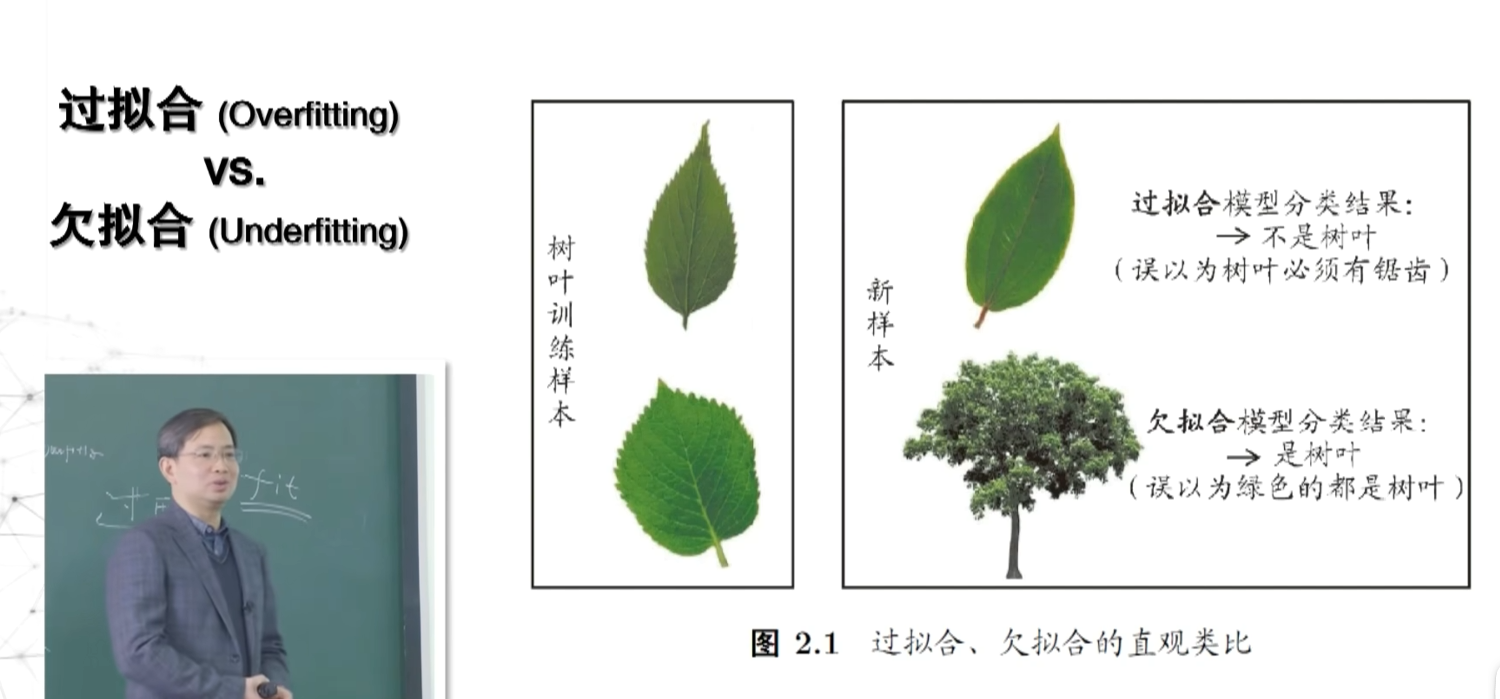
一、过拟合和欠拟合
泛化(generalization) :模型对未见样本的适应能力,即模型在新数据上的表现能力。
泛化误差:在"未来"样本上的误差
经验误差: 在训练数据集的误差,亦称为"训练误差"
二、三大问题

1、评估方法
矛盾:希望训练集大保证模型优良,也希望测试集大保证错误可能更小,选择模型之后,最后把所有的数据集再测试一遍

-
留出法

注意:
- 保持数据分布一致性(例如:分层采样)
- 多次重复划分(例如:100次随机划分) 目的:减少划分数据带来的误差
- 测试集不能太大、不能太小(例如:1/5----1/3) 目的:误差带来的差异太大
-
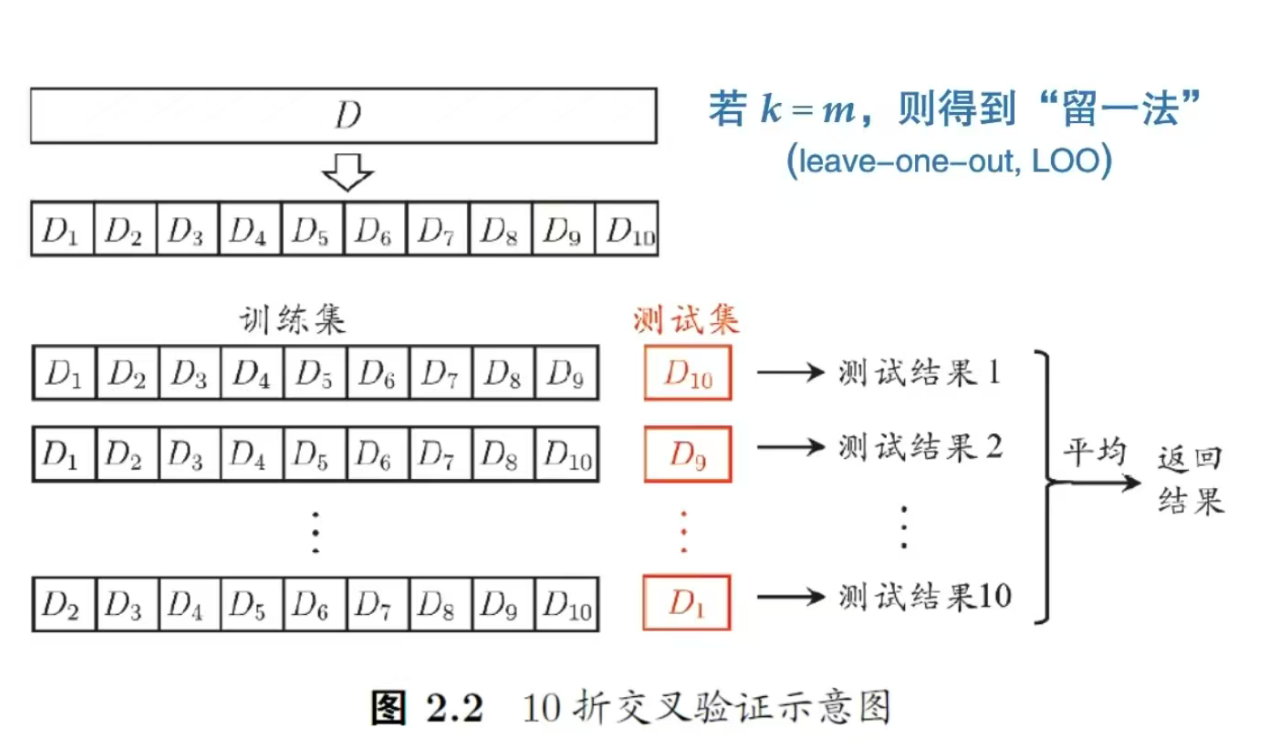
k--折交叉验证法
K折指的是平均划分数据集为几份,然后从从第一个份中再次随机切分,前面为训练集,最后一个为测试集,循环。最后结果平均该方法避免第一个方法的随机抽取。
-
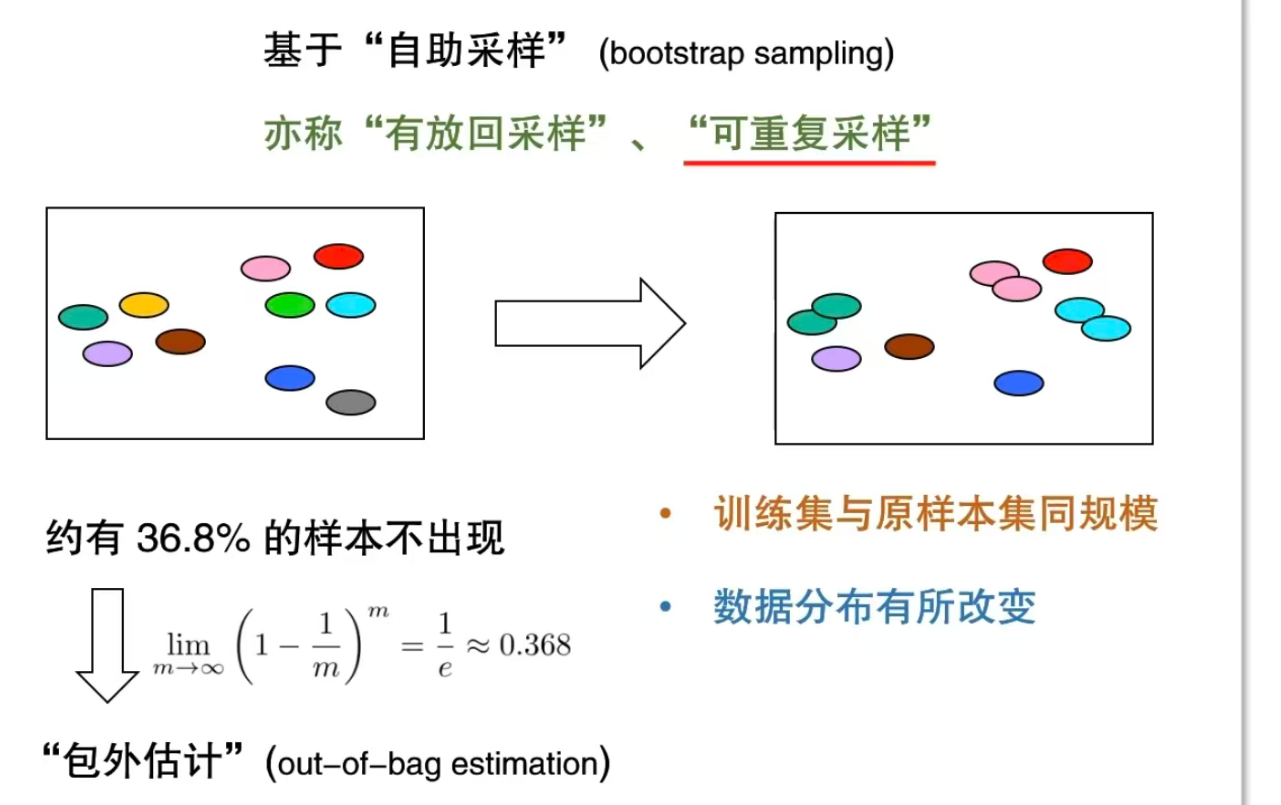
自助法
训练集和原样本集规模相同,但是分布改变
取出一个,复制一份放进原来的数据集。
大概26.8%作为测试集。
调参数和超参数
算法的参数:一般由人工设定,亦称为"超参数'
模型的参数:一般由学习确定
调参过程相似:先产生若干模型,然后基于某种评估方法进行选择
参数调的好不好对性能往往对最终性能有关键影响。
区别:
- 验证集:训练集中专门用于调参数的部分。
- 训练集:用于模型训练的集合
- 测试集:用于测试模型结果的集合
算法参数选定后,要用"训练集+验证集"重新训练最终模型
2、性能度量
性能度量是衡量模型泛化能力的评价标准,反映了任务需求,使用不同的性能度量往往会导致不同的评判结果
什么样的模型是"好"的,不仅取决于算法和数据,还取决于任务需求

这部分内容属于机器学习中模型性能评估的核心指标,我们可以从以下几个角度理解:
一、错误率与精度
- 错误率 :是模型在数据集D 上的错误预测样本数占总样本数的比例。公式中 I(f(xi)≠yi)\mathbb{I}(f(\boldsymbol{x}_i) \neq y_i)I(f(xi)=yi) 是指示函数,当模型预测值 f(xi)f(\boldsymbol{x}_i)f(xi) 与真实标签 yiy_iyi 不相等时,该函数取值为1,否则为0;( m ) 是数据集 ( D ) 的样本总数。
- 精度 :是模型在数据集DDD上的正确预测样本数占总样本数的比例,显然精度与错误率之和为1(acc(f;D)=1−E(f;D)\text{acc}(f;D) = 1 - E(f;D)acc(f;D)=1−E(f;D))。
二、混淆矩阵与查准率、查全率
-
混淆矩阵:是分类任务中用于可视化模型预测结果的表格,通过"真实情况"和"预测结果"的交叉组合,将样本分为四类:
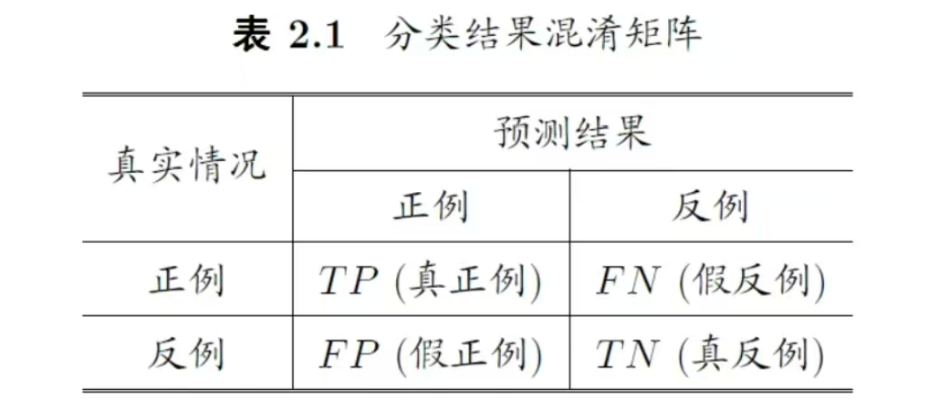
- ( TP )(真正例):真实为正例且预测为正例的样本数;
- ( FN )(假反例):真实为正例但预测为反例的样本数;
- ( FP )(假正例):真实为反例但预测为正例的样本数;
- ( TN )(真反例):真实为反例且预测为反例的样本数。
-
查准率(Precision,( P )) :也叫精确率,关注"预测为正例的样本中,真正是正例的比例",公式为 P=TPTP+FPP = \frac{TP}{TP + FP}P=TP+FPTP 。它衡量模型"预测的正例有多准"。
-
查全率(Recall,( R )) :也叫召回率,关注"真实为正例的样本中,被模型正确预测为正例的比例",公式为 R=TPTP+FNR = \frac{TP}{TP + FN}R=TP+FNTP。它衡量模型"对正例的覆盖能力有多强"。
三、F1度量
这部分内容是机器学习中用于综合评估分类模型性能的F1度量及带权重的( F_\beta )度量,具体解释如下:
(1)、F1度量
F1是查准率(( P ))和查全率(( R ))的调和平均数 ,用于平衡二者的性能表现,公式为: F1=2×P×RP+RF1 = \frac{2 \times P \times R}{P + R}F1=P+R2×P×R
也可转化为调和平均的形式: 1F1=12⋅(1P+1R)\frac{1}{F1} = \frac{1}{2} \cdot \left( \frac{1}{P} + \frac{1}{R} \right)F11=21⋅(P1+R1)
从混淆矩阵的角度,还可推导为: F1=2×TP样例总数+TP−TNF1 = \frac{2 \times TP}{\text{样例总数} + TP - TN}F1=样例总数+TP−TN2×TP
(其中( TP )为真正例,( TN )为真反例)
(2)、带偏好的( FβF_\betaFβ )度量
当对查准率和查全率有不同优先级时,使用 FβF_\betaFβ 度量,公式为: Fβ=(1+β2)×P×R(β2×P)+RF_\beta = \frac{(1 + \beta^2) \times P \times R}{(\beta^2 \times P) + R}Fβ=(β2×P)+R(1+β2)×P×R 对应的调和平均形式: 1Fβ=11+β2⋅(1P+β2R)\frac{1}{F_\beta} = \frac{1}{1 + \beta^2} \cdot \left( \frac{1}{P} + \frac{\beta^2}{R} \right)Fβ1=1+β21⋅(P1+Rβ2)
其中 β\betaβ 是权重参数,用于控制查准率和查全率的相对重要性:
- 若 β>1\beta > 1β>1 ,查全率( RRR )的影响更大;
- 若 β<1\beta < 1β<1 ,查准率( PPP )的影响更大。
3、比较检验
在某种度量下取得评估结果后,是否可以直接比较以评判优劣? NO!
因为:
- 测试性能不等于泛化性能
- 测试性能随着测试集的变化而变化
- 很多机器学习算法本身有一定的随机性
机器学习----------------------------> "概率近似正确"
常用方法:
统计假设检验为学习器性能比较提供了重要依据
两学习器的比较: ------------------------>统计显著性
- 交叉验证t检验(基于成对t检验): k折交叉验证;5*2交叉验证
- ++McNemar检验(基于列联表,卡方检验)++
