文章目录
跳表 skiplist
跳表本质也是一个用于快速查找的概率型数据结构,通过在有序链表上增加多级索引来实现。有了这些索引,快表查询的效率接近于二分 ,在一些场景上可以代替平衡二叉树如AVL树、红黑树等。
为什么一个有序的链表查找效率会这么高呢?不同于数组查找,链表查找是不能直接用左右边界求mid来二分的。下面我们先分析其原因。
跳表的结构特点
-
多级索引:跳表在最底层是一个有序链表,底层的链表包含所有数据元素。每一层索引是下层索引的子集。通常每个元素以一定概率 p 选取是否出现在上一层索引中。
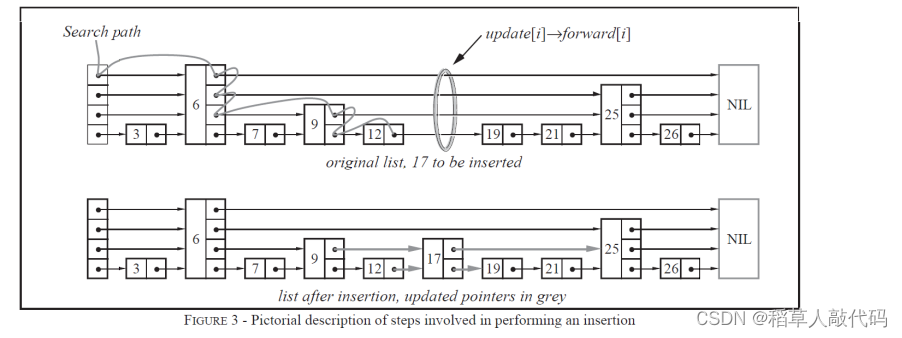
对于跳表中的每一个节点,都会有多个且数目不相同的指针指向后面的元素。越高层的指针指向的数据更远也更大,这样一来,查找某一个数据时就不用遍历整个链表了,而是通过指针(也称为索引)越级查询。
-
随机层数:每个节点的多个指针指向的值从大到小竖直排列,有效指针的数量就是节点的层数。插入一个新元素时,从最低层开始插入,然后以概率 p 决定是否在上一层也插入该元素。如果决定插入,则继续在上一层进行,直至不再插入或达到最高层。
-
平衡性:随机化层数使得节点在每一层索引上的分布大致均匀,保证了多级索引的有效性,确保大部分操作的时间复杂度保持在 O(logn)。
为什么新节点的层数要是随机的呢?
如果新节点的层数是固定的,跳表的结构就退化成了一个简单的有序链表,假设每个节点的层数是2,这样的跳表的时间复杂度查找、删除、添加的时间复杂度都是O(N)的。同样的,如果每个节点的层数
都很大,那么遍历一个节点的所有下级索引的代价也就越大,同样时间复杂度还是会退化成O(N)。所以,我们需要一种方案,使得有序链表中的层数不是固定的,且高层数的节点不能太多。这样一来,就可以通过设计一个随机层数的概率来大概控制整个有序链表的效率。
具体的,高层索引节点进行大跨度的跳跃,快速接近目标节点,然后在底层进行细致查找。这种多级索引结构使得查找、插入和删除操作的时间复杂度为
O(logn)。当然,由于是随机产生层数,最坏情况就是每个节点只有一层或者每个节点的层数都是节点的总数,这样查找等操作时间复杂度就退化到了O(N).想要更具体的性能分析,可以去看大佬的博客:铁蕾大佬
跳表的具体实现
参考题目:leetcode1206. 设计跳表
代码实现:
cpp
#define _CRT_SECURE_NO_WARNINGS 1
struct SkilpListNode {
int _val;
vector<SkilpListNode*> _nextv;
SkilpListNode(int val, int level)
:_val(val)
, _nextv(level, nullptr)
{
}
};
class Skiplist {
public:
typedef SkilpListNode Node;
Skiplist() {
srand(time(NULL));//设置随机数种子
_head = new Node(-1, 1);//头节点,层数为1
}
bool search(int target) {
Node* cur = _head;
int level = _head->_nextv.size() - 1;
while (level >= 0) {
//层数从高往低开始
if (cur->_nextv[level] && target > cur->_nextv[level]->_val) {
cur = cur->_nextv[level];//如果目标值大于当前节点的第level层索引的值,可以跳过去,更新cur
}
else if (!cur->_nextv[level] || target < cur->_nextv[level]->_val) {
level--;//下一个索引节点是空
//如果目标值小于当前节点的第level层索引的值,往下层移动,也就是再去比较值更小的下级索引
}
else {
return true;//找到目标值
}
}
return false;
}
vector<Node*> FindPrevNode(int num) {
Node* cur = _head;
int level = _head->_nextv.size() - 1;
vector<Node*> prev(level + 1, _head);//用一个数组存下新节点的所有层的前一个节点
while (level >= 0) {
//层数从高往低开始
if (cur->_nextv[level] && num > cur->_nextv[level]->_val) {
cur = cur->_nextv[level];
}
else if (!cur->_nextv[level] || num <= cur->_nextv[level]->_val) {
prev[level] = cur;
level--;
}
}
return prev;
}
void add(int num) {
vector<Node*> prev = FindPrevNode(num);
int n = GetRandomLevel();
Node* newnode = new Node(num, n);
if (n > _head->_nextv.size()) {
_head->_nextv.resize(n, nullptr);
prev.resize(n, _head);
}
for (int i = 0; i < n; i++) {
newnode->_nextv[i] = prev[i]->_nextv[i];
prev[i]->_nextv[i] = newnode;
}
}
bool erase(int num) {
vector<Node*> prev = FindPrevNode(num);
if (prev[0]->_nextv[0] == nullptr || prev[0]->_nextv[0]->_val != num) {
return false;
}
Node* delnode = prev[0]->_nextv[0];
int n = delnode->_nextv.size();
for (int i = 0; i < n; i++) {
prev[i]->_nextv[i] = delnode->_nextv[i];
}
delete delnode;
//如果删除的节点是最高层数
int i = _head->_nextv.size() - 1;
while (i >= 0) {
if (_head->_nextv[i] == nullptr) {
--i;
}
else break;
}
_head->_nextv.resize(i + 1);
return true;
}
int GetRandomLevel() {
size_t level = 1;
while (rand() <= RAND_MAX * _p && level < _maxlevel) {
level++;
}
return level;
}
private:
Node* _head;
size_t _maxlevel = 32;
double _p = 0.25;//增加层数的概率
};
/**
* Your Skiplist object will be instantiated and called as such:
* Skiplist* obj = new Skiplist();
* bool param_1 = obj->search(target);
* obj->add(num);
* bool param_3 = obj->erase(num);
*/