神经网络与注意力机制的权重学习对比:公式探索
注意力机制与神经网络权重学习的核心差异
在探讨神经网络与注意力机制的权重学习时,一个核心差异在于它们如何处理输入数据的权重。神经网络通常通过反向传播算法学习权重,而注意力机制则通过学习数据的"重要性"权重来增强模型的性能。
这里,我们重点探讨注意力机制中的关键公式及其推导。
注意力机制的核心公式
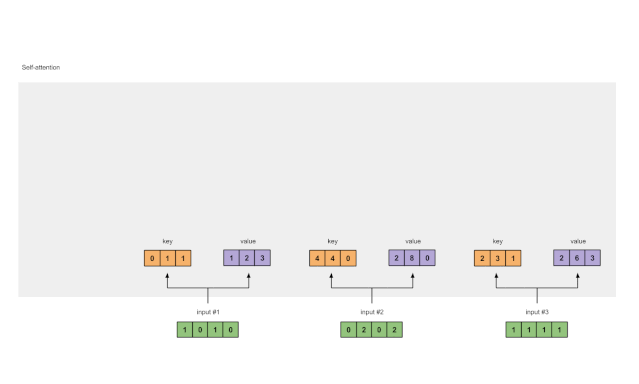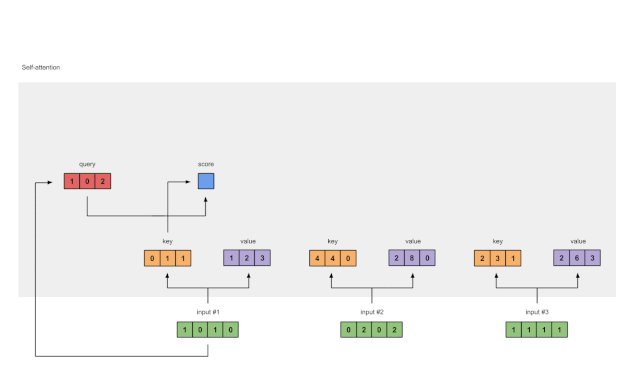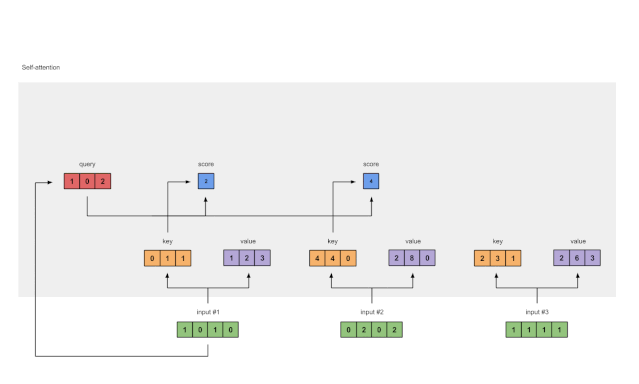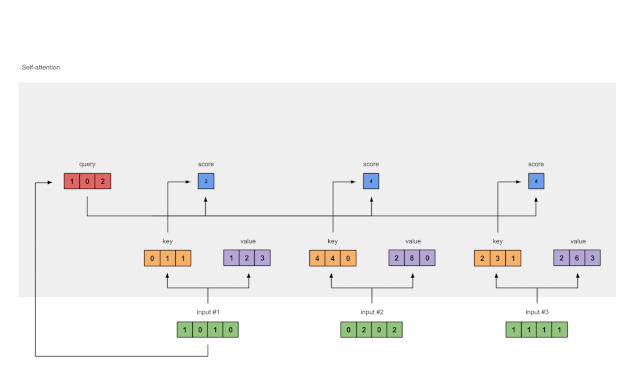
注意力机制的核心在于计算查询( Q Q Q)和键( K K K)之间的相似度,并用这个相似度去加权值( V V V)。公式如下:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dk QKT)V
其中, Q Q Q是查询矩阵, K K K是键矩阵, V V V是值矩阵, d k d_k dk是键向量的维度。
通俗解释
在注意力机制中,我们想要知道哪些输入数据对当前的输出更重要。查询( Q Q Q)和键( K K K)的点积可以帮助我们计算这种"重要性"。但是,当数据的维度很高时,点积的结果可能变得非常大,使得softmax函数难以处理。因此,我们引入了一个缩放因子 1 d k \frac{1}{\sqrt{d_k}} dk 1来调整点积的结果,使其更适合softmax函数处理。最后,我们用softmax的结果作为权重去加权值( V V V),得到最终的输出。
具体来说:
| 项目 | 描述 |
|---|---|
| 查询( Q Q Q) | 表示当前的输入或状态,用于与键进行匹配。 |
| 键( K K K) | 表示所有的输入数据,与查询进行匹配以计算重要性。 |
| 值( V V V) | 表示与键相对应的实际数据,用于最终的加权输出。 |
| 点积 | 查询和键的点积表示它们之间的相似度或"重要性"。 |
| 缩放因子 | 用于调整点积结果,使其适合softmax函数处理。 |
| softmax函数 | 将相似度转换为概率分布,表示不同数据的重要性。 |
公式推导
-
计算相似度 :
首先,计算查询( Q Q Q)和键( K K K)的点积,得到相似度矩阵 S S S:
S = Q K T S = QK^T S=QKT -
引入缩放因子 :
为了防止点积结果过大,引入缩放因子 1 d k \frac{1}{\sqrt{d_k}} dk 1:
S ^ = S d k \hat{S} = \frac{S}{\sqrt{d_k}} S^=dk S -
应用softmax函数 :
将缩小的相似度矩阵 S ^ \hat{S} S^输入到softmax函数中,得到概率分布矩阵 A A A:
A = softmax ( S ^ ) A = \text{softmax}(\hat{S}) A=softmax(S^) -
加权输出 :
最后,用softmax的输出 A A A作为权重去加权值( V V V),得到最终的输出 O O O:
O = A V O = AV O=AV
#注意力机制
#神经网络
#权重学习
#点积相似度
#缩放因子
#softmax函数