【通俗理解】马尔科夫毯:信息屏障与状态独立性的守护者
马尔科夫毯的通俗比喻
- 你可以把马尔科夫毯想象成一个"信息屏障",它隔绝了系统内部与外部的信息交流。
- 在这个屏障之内,系统的状态是独立的,不受外界影响。
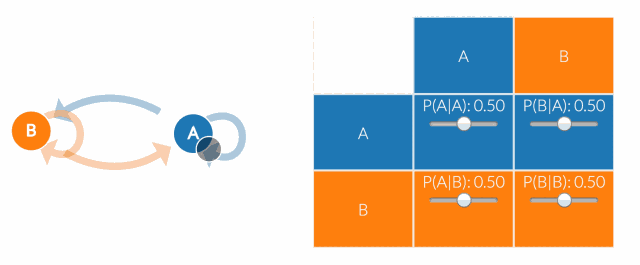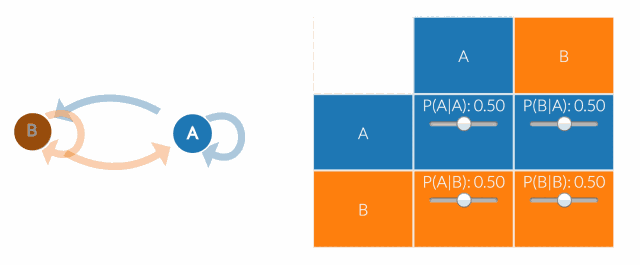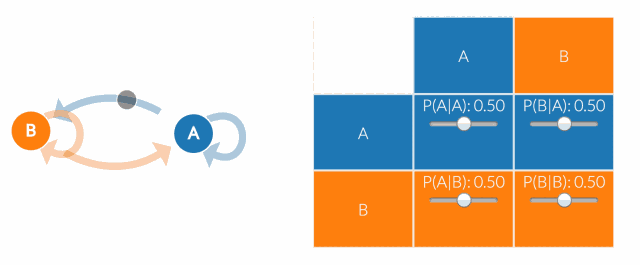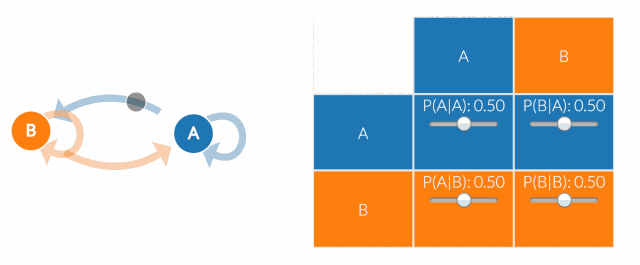
马尔科夫毯的核心概念与应用
| 组件/步骤 | 描述 |
|---|---|
| 马尔科夫毯 | 在概率图模型中,一个节点的马尔科夫毯包含了这个节点的所有邻居节点以及这些邻居节点之间的连接。 |
| 信息屏障 | 马尔科夫毯形成了一个屏障,使得节点在给定其马尔科夫毯的条件下,与图中的其他部分独立。 |
| 状态独立性 | 在马尔科夫毯的屏障之内,节点的状态是独立的,不受外部节点的影响。 |
其基本定义可通过以下公式体现:
P ( X i ∣ X rest ) = P ( X i ∣ MB ( X i ) ) P(X_i | X_{\text{rest}}) = P(X_i | \text{MB}(X_i)) P(Xi∣Xrest)=P(Xi∣MB(Xi))
其中, X i 是图中的某个节点, X rest 是图中除了 X i 以外的所有节点,MB ( X i ) 是 X i 的马尔科夫毯 \text{其中,} X_i \text{ 是图中的某个节点,} X_{\text{rest}} \text{ 是图中除了 } X_i \text{ 以外的所有节点,} \text{MB}(X_i) \text{ 是 } X_i \text{ 的马尔科夫毯} 其中,Xi 是图中的某个节点,Xrest 是图中除了 Xi 以外的所有节点,MB(Xi) 是 Xi 的马尔科夫毯
| 项目 | 描述 |
|---|---|
| 节点 | X i X_i Xi,概率图模型中的一个变量或实体。 |
| 其余节点 | X rest X_{\text{rest}} Xrest,概率图模型中除了 X i X_i Xi 以外的所有节点。 |
| 马尔科夫毯 | MB ( X i ) \text{MB}(X_i) MB(Xi),包含 X i X_i Xi 的所有邻居节点以及这些邻居节点之间的连接。 |
通俗解释与案例
-
马尔科夫毯的直观理解
- 想象一个社交网络,其中每个人(节点)都只关心他们的直接朋友(邻居节点)以及这些朋友之间的关系(邻居节点之间的连接)。
- 在这个网络中,一个人的马尔科夫毯就是他们的朋友圈,给定这个人的朋友圈,这个人的状态(比如心情、活动等)就只与他们的朋友圈有关,与社交网络中的其他人无关。
-
马尔科夫毯的应用价值
- 在机器学习和数据科学中,马尔科夫毯可以帮助我们理解变量之间的依赖关系,从而简化模型和提高计算效率。
- 在概率推理中,马尔科夫毯可以用来减少需要考虑的变量数量,从而简化推理过程。
-
马尔科夫毯的优势
- 通过利用马尔科夫毯,我们可以更有效地进行概率推理和计算,因为只需要考虑与当前节点直接相关的节点和连接。
- 马尔科夫毯也提供了一个直观的方式来理解变量之间的依赖和独立性。
-
马尔科夫毯的类比
- 你可以把马尔科夫毯比作一个"隔音墙",它隔绝了房间内的声音与房间外的声音。
- 在这个隔音墙之内,房间内的声音是独立的,不受外界声音的影响。
具体来说:
| 项目 | 描述 |
|---|---|
| 节点 | X i X_i Xi,就像是房间内的一个人,他们的状态(比如说话声)只与房间内的环境有关。 |
| 其余节点 | X rest X_{\text{rest}} Xrest,就像是房间外的人,他们的状态对房间内的人没有影响。 |
| 马尔科夫毯 | MB ( X i ) \text{MB}(X_i) MB(Xi),就像是隔音墙,它隔绝了房间内外的声音交流。 |
公式探索与推演运算
-
基本公式:
- P ( X i ∣ X rest ) = P ( X i ∣ MB ( X i ) ) P(X_i | X_{\text{rest}}) = P(X_i | \text{MB}(X_i)) P(Xi∣Xrest)=P(Xi∣MB(Xi)):表示节点 X i X_i Xi 在给定其余节点 X rest X_{\text{rest}} Xrest 的条件下的概率,等于 X i X_i Xi 在给定其马尔科夫毯 MB ( X i ) \text{MB}(X_i) MB(Xi) 的条件下的概率。
-
具体计算:
- 假设我们有一个概率图模型,其中包含节点 X 1 , X 2 , X 3 , X 4 X_1, X_2, X_3, X_4 X1,X2,X3,X4,且 X 2 X_2 X2 是 X 1 X_1 X1 的马尔科夫毯。
- 那么,根据马尔科夫毯的性质,我们有 P ( X 1 ∣ X 2 , X 3 , X 4 ) = P ( X 1 ∣ X 2 ) P(X_1 | X_2, X_3, X_4) = P(X_1 | X_2) P(X1∣X2,X3,X4)=P(X1∣X2)。
-
与概率推理的关系:
- 在进行概率推理时,我们可以利用马尔科夫毯来减少需要考虑的变量数量。
- 具体来说,如果我们要计算某个节点的概率,我们只需要考虑这个节点的马尔科夫毯,而不需要考虑整个图中的所有节点。
关键词提炼
#马尔科夫毯
#信息屏障
#状态独立性
#概率图模型
#节点
#邻居节点
#概率推理