OpenCV|超详细的几何变换

2D图像几何变换的3×3矩阵：

图像常见的几何变换：

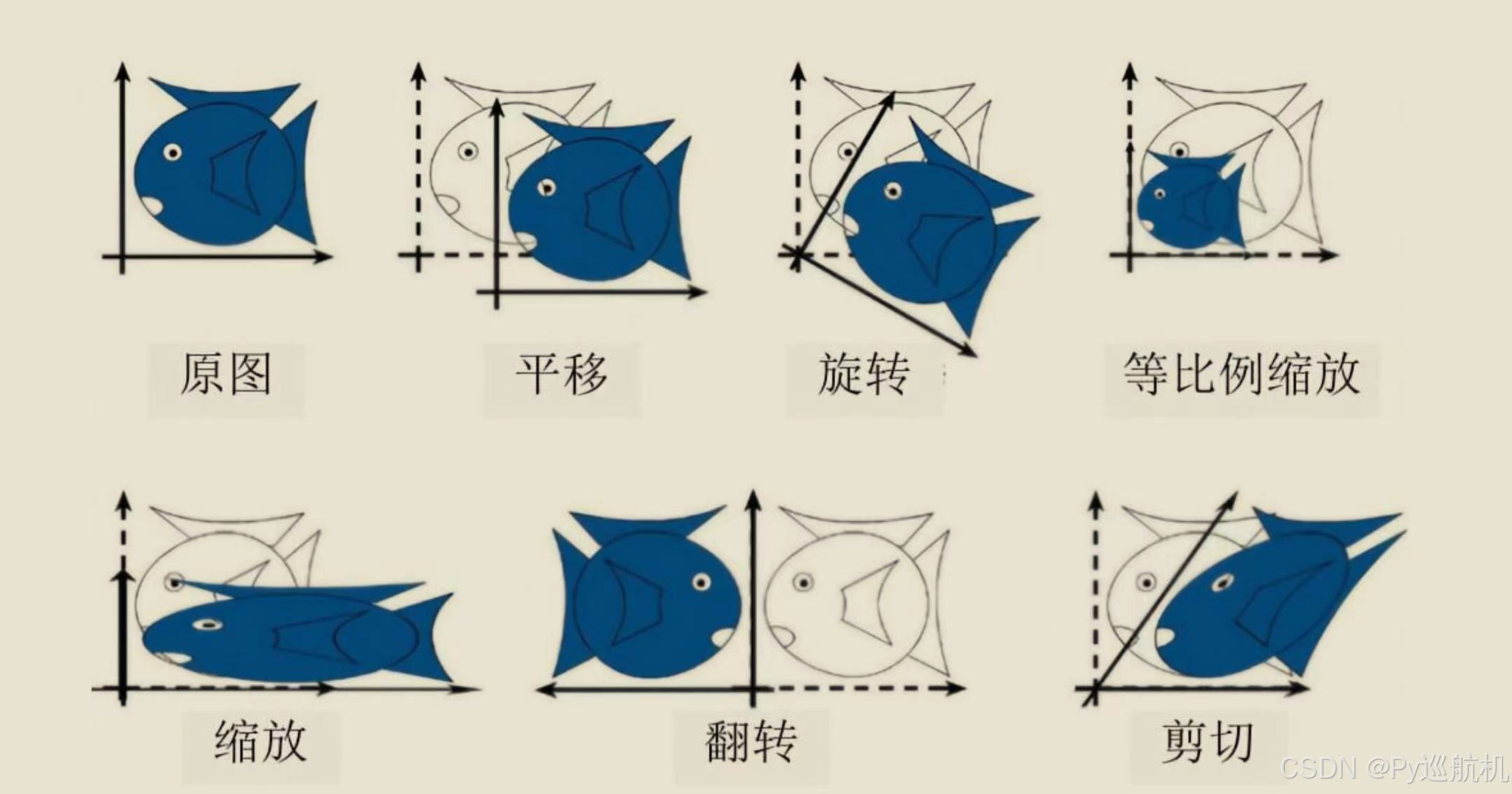
图像来源：《OpenCV 4.5计算机视觉开发实战：基于Python》作者：朱文伟李建英；

1. 平移（Translation）

在OpenCV中，平移不是直接通过一个函数完成的，而是先通过创建一个平移矩阵，然后使用warpAffine函数应用这个矩阵。

cv2.getTranslationMatrix2D(center, offset, scale)

center：源图像中的变换中心。
offset：沿x和y方向移动的距离。
scale：通常设置为1.0，因为平移不涉及缩放。

返回的矩阵然后传递给warpAffine函数进行实际的平移操作。

2. 旋转（Rotation）

cv2.getRotationMatrix2D(center, angle, scale)

center：旋转中心。
angle：旋转角度，以度为单位。正值表示逆时针旋转。
scale：图像缩放比例。

这个函数返回一个2x3的旋转矩阵，该矩阵可以传递给warpAffine进行图像的旋转。

图像旋转后显示完整图像****示例代码：

import cv2  
import numpy as np  
  
def rotate_image(image, angle):  
    # 获取图像尺寸  
    (h, w) = image.shape[:2]  
      
    # 计算图像中心  
    center = (w // 2, h // 2)  
      
    # 获取旋转矩阵（注意角度需要转换为弧度）  
    M = cv2.getRotationMatrix2D(center, angle, 1.0)  
      
    # 计算旋转后图像的边界框  
    cos = np.abs(M[0, 0])  
    sin = np.abs(M[0, 1])  
    nW = int((h * sin) + (w * cos))  
    nH = int((h * cos) + (w * sin))  
  
    # 调整旋转矩阵以考虑平移  
    M[0, 2] += (nW / 2) - center[0]  
    M[1, 2] += (nH / 2) - center[1]  
  
    # 执行旋转  
    rotated = cv2.warpAffine(image, M, (nW, nH))  
      
    return rotated  
  
# 读取图像  
image = cv2.imread('your_image.jpg')  
  
# 旋转图像，例如旋转45度  
rotated_image = rotate_image(image, 45)  
  
# 显示原始和旋转后的图像  
cv2.imshow("Original Image", image)  
cv2.imshow("Rotated Image", rotated_image)  
cv2.waitKey(0)  
cv2.destroyAllWindows()

3. 缩放（Resizing）

缩放通常使用resize函数，而不是通过几何变换矩阵。

cv2.resize(src, dsize, fx=0, fy=0, interpolation=cv2.INTER_LINEAR)

src：输入图像。
dsize：输出图像的大小。这是一个宽度和高度的元组。如果它是零，则通过fx和fy计算大小。
fx、fy：沿x轴和y轴的缩放比例。
interpolation：插值方法，用于确定如何计算输出图像中的像素值。

4. 仿射变换（Affine Transformation）

仿射变换是一个更一般的变换，包括旋转、平移、缩放和倾斜。

cv2.warpAffine(src, M, dsize, flags=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(0,0,0))

src：输入图像。
M：2x3的变换矩阵。
dsize：输出图像的大小。
flags：插值方法。
borderMode：边界像素模式。
borderValue：当borderMode=cv2.BORDER_CONSTANT时，边界像素的值。

5. 透视变换（Perspective Transformation）

透视变换用于从一个视角转换到另一个视角，需要一个3x3的变换矩阵。

cv2.warpPerspective(src, M, dsize, flags=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(0,0,0))

参数与warpAffine相似，但M是一个3x3的透视变换矩阵。

6 图像金字塔（Image Pyramid）

在Python的OpenCV库中，图像金字塔（Image Pyramid）是一种用于图像多尺度表达的有效结构，主要用于图像特征检测、图像分割和图像压缩等领域。图像金字塔通过逐步减小图像的分辨率来创建一系列图像，这些图像以金字塔形状排列，层级越高，图像越小，分辨率越低。

OpenCV提供了两个主要的函数来实现图像金字塔的构建：cv2.pyrDown()和cv2.pyrUp()。

1. cv2.pyrDown(src[, dst[, dstsize[, borderType]]])

功能：对图像进行下采样（缩小），生成图像金字塔的下一层。

参数解释：

src：输入图像，即当前层的图像。
dst：输出图像，即下采样后的图像。这是一个可选参数，如果提供，则输出图像会存储在这里。
dstsize：输出图像的大小。如果此参数为0（默认值），则输出图像的尺寸将是输入图像尺寸的一半（宽度和高度都减半）。
borderType：边界像素的插值方法。在大多数情况下，使用默认值cv2.BORDER_DEFAULT即可。

返回值 ：下采样后的图像。如果提供了dst参数，则函数返回None；否则，返回下采样后的图像。

2. cv2.pyrUp(src[, dst[, dstsize[, borderType]]])

功能：对图像进行上采样（放大），尝试从图像金字塔的下一层重建当前层。但需要注意的是，上采样并不是下采样的完全逆操作，因为上采样过程中会丢失一些信息，导致重建的图像比原始图像模糊。

参数解释：

src：输入图像，即金字塔下一层的图像。
dst：输出图像，即上采样后的图像。这是一个可选参数，如果提供，则输出图像会存储在这里。
dstsize：输出图像的大小。如果此参数为0（默认值），则输出图像的尺寸将是输入图像尺寸的两倍（宽度和高度都加倍）。但通常建议明确指定dstsize，以匹配原始图像的尺寸或所需的尺寸。
borderType：边界像素的插值方法。在大多数情况下，使用默认值cv2.BORDER_DEFAULT即可。

返回值 ：上采样后的图像。如果提供了dst参数，则函数返回None；否则，返回上采样后的图像。

7 图像翻转（Flipping）

cv2.flip(src, flipCode)

src：输入图像，即你想要翻转的图像。
flipCode：指定翻转方向的标志。它是一个整数，决定了图像翻转的方式。
- 当flipCode为0时，表示沿x轴翻转（即上下翻转），实际上这并不会改变图像，因为x轴是水平的，而翻转通常是相对于垂直轴（y轴）或水平轴（但在这里不适用，因为x轴翻转在视觉上没有效果，除非你改变了坐标系统的解释）。但这里通常理解为参数设置错误或不适用于此上下文。
- 当flipCode > 0时（通常是1），表示沿y轴翻转（即左右翻转）。
- 当flipCode < 0时（通常是-1），表示沿x轴和y轴同时翻转（即上下左右翻转，相当于180度旋转）。
  
  import cv2
  
  读取图像
  
  img = cv2.imread('your_image_path.jpg')
  
  左右翻转图像
  
  flipped_img_lr = cv2.flip(img, 1)
  
  上下左右翻转图像（180度旋转）
  
  flipped_img_udlr = cv2.flip(img, -1)
  
  显示原图和翻转后的图像
  
  cv2.imshow('Original Image', img)
  cv2.imshow('Flipped Left-Right', flipped_img_lr)
  cv2.imshow('Flipped Up-Down and Left-Right', flipped_img_udlr)
  
  cv2.waitKey(0)
  cv2.destroyAllWindows()