零样本学习允许AI系统对未明确训练过的类别进行图像分类,标志着计算机视觉和机器学习的重大进步。本文将介绍使用CLIP实现零样本图像分类的详细分步指南,从环境设置到最终的图像处理和分类。我们首先介绍零样本学习的概念及其在现代AI应用中的重要性。然后深入探讨CLIP模型的概述,解释其架构以及其强大的跨模态学习能力背后的原理。最后用一个实际的实现样例来介绍,设置工作环境、加载CLIP模型和处理器以及准备图像进行分类的基本步骤。
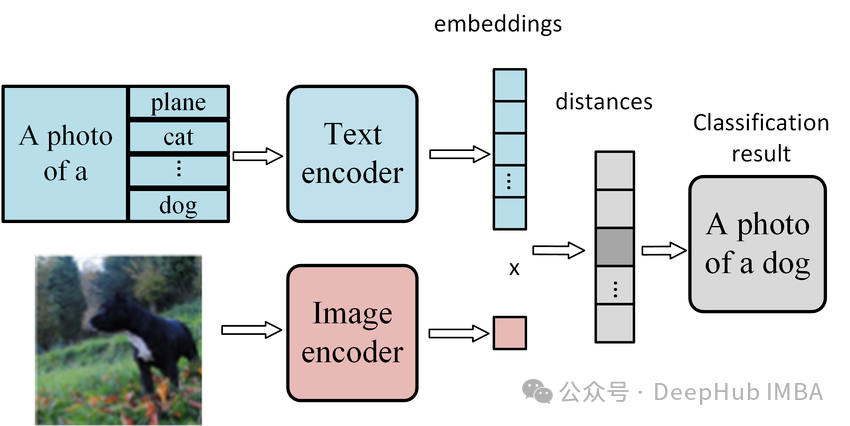
1、零样本图像分类简介
零样本图像分类是一涉及使用未经明确训练的特定类别的模型将图像分类到不同的类别中的任务。模型的任务是预测图像所属的类别。
当只有少量标记数据,或者想要快速将图像分类整合到应用程序中时,这很有用。我们可以使用预先存在的预训练模型,而不是训练自定义模型。这些模型通常是多模态的,并且已经在大量的图像和描述数据集上进行了训练,它们可以用于许多不同的任务。
我们只需要给模型一些关于它没有见过的类别的额外信息(这被称为辅助信息,可以是描述或属性),模型就能够预测未见到的分类,零样本分类是迁移学习的一个子领域。
零样本图像分类任务包括在推理时根据自己的标签对图像进行分类。例如,可以传递一个标签列表,如飞机、汽车、狗、鸟,以及您想要分类的图像。模型将选择最可能的标签。
对比语言-图像预训练(CLIP)是零样本分类最流行的模型之一。它可以根据图像的常见对象或特征对图像进行分类,不需要为每个新用例进行微调。
2、CLIP模型概述

CLIP是一个从自然语言监督中学习视觉概念的神经网络。它在图像和文本对上进行训练,学会预测与给定图像相对应的文本。然后它可以用于新图像的零样本分类。
CLIP具有灵活性,可以应用于各种视觉分类基准。它不需要针对基准的性能进行优化,并且在表示学习评估中使用线性探针时,已经显示出最先进的性能和分布鲁棒性。它在表示学习评估中使用线性探针时优于现有模型,如ImageNet。
该网络由一个图像编码器和一个文本编码器组成,它们被联合训练以预测正确的配对。在训练过程中,图像和文本编码器被训练以最大化真实配对的图像和文本嵌入的余弦相似度,同时最小化不正确配对的余弦相似度。
CyCLIP是一个建立在CLIP基础上的框架,它形式化了一致性。它优化学习到的表示,使其在图像和文本空间中在几何上保持一致,并且已经被证明可以提高CLIP的性能。
3、设置环境
我们从设置工作环境开始。首先下载本文中将使用的包。
!pip install transformers
!pip install torch4、加载模型和处理器
我们需要两个主要组件来构建零样本图像分类:模型 和处理器 。让我们首先从Transformers加载CLIP模型。要加载模型,我们将使用
from_pretrained方法,并传递此特定任务的正确检查点。
model = CLIPModel.from_pretrained(
"./models/openai/clip-vit-large-patch14") 然后使用Hugging Face的Transformers库为clip模型加载一个预训练的处理器
from transformers import AutoProcessor
processor = AutoProcessor.from_pretrained(
"./models/openai/clip-vit-large-patch14")5、加载和显示图像
为了加载图像,我们将使用PIL库并导入Image类。使用
Image.open加载图像,并指定图像的路径。
from PIL import Image
image = Image.open("./occupiers.png")
image
6、定义标签和输入
创建标签。我们可以使用"占领者的照片 "作为第一个标签,"猫的照片"作为第二个标签。
labels = ["a photo of a occupiers", "a photo of a cats"]然后创建模型的输入。这里将使用处理器。我们需要传递文本(即标签)和图像。
inputs = processor(text=labels,
images=image,
return_tensors="pt",
padding=True)7、处理和分类图像
我们将上面的预处理内容输入模型
outputs = model(**inputs) 结果如下:
CLIPOutput(loss=None, logits_per_image=tensor([[21.8763, 9.7856]], grad_fn=<TBackward0>), logits_per_text=tensor([[21.8763],
[ 9.7856]], grad_fn=<MulBackward0>), text_embeds=tensor([[-2.9747e-03, 2.6380e-03, 3.2704e-04, ..., -1.7559e-02,
-7.0350e-05, 3.6619e-03],
[-1.9645e-02, 2.0558e-02, 2.9485e-02, ..., 3.1643e-02,
1.4714e-02, 6.7246e-03]], grad_fn=<DivBackward0>), image_embeds=tensor([[ 5.7789e-03, -4.3962e-02, -3.9901e-03, 5.6101e-02, 6.3676e-03,
2.9096e-02, 2.6953e-02, 4.0592e-02, -8.4450e-06, 5.8055e-03,
-1.4274e-02, -3.1642e-02, 2.4113e-02, -2.4111e-02, -1.1296e-02,
9.6764e-03, 1.0219e-02, 8.4689e-03, 3.4425e-02, 1.2221e-02,
2.7957e-02, 3.0495e-02, 1.3093e-02, 1.7346e-02, 5.5131e-03,
-2.7130e-02, -5.8669e-02, -2.7784e-02, -4.0745e-02, -3.3350e-02,
-2.0706e-02, 2.8432e-02, 5.9084e-03, 5.6609e-03, -9.2576e-03,
1.0789e-02, 2.0793e-02, -4.7598e-03, 2.2963e-02, -3.3255e-02,
-1.6315e-02, -2.4104e-02, 1.5616e-02, 3.3750e-02, -2.6935e-02,
8.7083e-03, 2.1546e-03, -3.3888e-02, 4.7085e-02, -3.9901e-03,
-1.2575e-02, -5.2894e-02, 3.6603e-02, -7.6685e-03, 2.7837e-02,
3.0959e-02, 2.0127e-02, -2.4038e-02, -2.8744e-02, -1.4038e-02,
1.5173e-02, 1.8799e-02, -2.9608e-03, -2.2345e-02, 4.7702e-02,
-1.4433e-02, 1.4635e-02, 3.1230e-02, 5.9901e-02, -1.3265e-03,
7.6162e-03, 1.2988e-02, 5.5220e-03, 1.4117e-02, -1.4327e-02,
2.1601e-03, -1.1008e-02, -3.7867e-02, 1.6744e-02, 1.1719e-02,
1.8613e-02, 3.0909e-02, 3.1654e-02, 2.1501e-02, 7.9533e-03,
1.0662e-02, -1.1237e-02, -4.3277e-02, 2.6244e-02, 1.2052e-02,
4.5038e-02, -2.9739e-02, -1.0173e-02, -6.4970e-03, -4.3230e-03,
5.1218e-03, -3.4656e-02, -6.2149e-02, 8.0739e-03, 4.5069e-02,
-1.3734e-02, -1.9803e-02, 1.0912e-03, -5.1993e-02, -2.2205e-02,
1.8498e-02, -2.1908e-02, -4.6194e-03, 3.1051e-04, -3.7240e-03,
1.7533e-02, 1.6989e-02, -4.8901e-02, 1.3751e-02, 6.9713e-03,
2.8202e-02, 2.1325e-02, -3.6354e-02, -7.1071e-02, -2.9884e-02,
-2.0108e-03, -3.9210e-02, 1.8043e-02, 2.5318e-02, 2.7652e-02,
-1.6892e-02, -2.4670e-02, -5.6512e-03, -1.4796e-02, 9.8687e-03,
-1.7640e-02, 8.6374e-02, 7.8690e-03, 7.9550e-04, -4.2292e-02,
9.5068e-02, 5.3002e-03, 7.0152e-03, -1.5667e-02, -2.9754e-02,
1.6179e-02, 4.1414e-02, -3.3988e-02, -6.1861e-02, -4.3325e-03,
2.5685e-04, 4.3989e-03, -5.8877e-03, 1.1796e-02, 1.5167e-02,
-5.2949e-02, 2.1775e-02, 2.7675e-02, 2.2198e-02, 1.7648e-02,
-3.4697e-02, 7.0108e-03, 5.2061e-02, -1.1802e-02, 1.5102e-02,
-1.4692e-02, -5.4631e-03, -2.1430e-02, -9.3270e-04, 2.9920e-02,
-2.4192e-02, -2.3823e-02, 9.7590e-03, 7.7101e-03, 1.7580e-03,
3.9310e-03, -9.8752e-03, -8.6602e-03, 4.7450e-02, 2.0988e-02,
3.0213e-02, -1.6734e-02, -1.8952e-01, -6.4087e-02, 3.9655e-02,
4.8678e-02, 1.7897e-03, 6.5058e-03, 3.5143e-02, -3.7138e-02,
8.1137e-03, -3.1982e-02, -7.0958e-03, 6.4963e-03, 1.4733e-02,
4.0858e-03, -1.5045e-02, 5.5016e-03, -1.3627e-02, -3.6162e-03,
-1.3287e-02, -6.2757e-02, -1.3430e-03, -2.7292e-05, 6.0769e-04,
1.2674e-02, 8.1904e-03, 8.9082e-03, 1.9957e-02, 3.8102e-03,
3.6519e-03, -4.4056e-02, -1.5661e-02, -9.5863e-03, -2.4219e-03,
8.5753e-03, 1.6604e-02, -2.0069e-02, -4.6871e-02, 2.4206e-02,
-4.8668e-03, 1.1664e-02, -6.8940e-03, -1.3681e-02, 1.6395e-02,
9.4232e-03, -3.0263e-02, 3.2366e-03, 4.0138e-02, -6.1738e-03,
-3.2676e-02, -1.8601e-02, 1.7904e-02, -1.3817e-02, -1.8048e-02,
5.5864e-03, 1.0975e-02, -1.4123e-02, -3.0170e-02, 3.3311e-02,
4.9997e-03, -1.0391e-02, 3.1777e-03, 1.9882e-02, 6.2273e-03,
-3.2720e-02, -4.0859e-02, 1.5610e-02, -1.6431e-02, -3.8654e-03,
8.7215e-02, -3.3904e-02, 6.1722e-03, -3.5134e-02, -1.6150e-02,
1.4944e-02, -2.3586e-02, -1.0361e-02, 3.7658e-03, -3.6290e-02,
-8.9540e-03, -1.3771e-02, -6.8122e-03, 3.0026e-03, -4.5137e-02,
6.4355e-03, -3.3159e-03, -1.5333e-02, 3.4441e-02, -1.5725e-02,
1.1518e-02, -5.9313e-03, 4.2979e-02, 2.8261e-02, 4.7787e-03,
3.1031e-02, 1.7139e-03, 1.6778e-02, 2.6897e-04, -2.6202e-02,
5.4559e-02, 7.4263e-04, -4.5143e-03, 1.2781e-03, 1.4802e-02,
-3.7519e-03, 3.3716e-02, -2.1538e-02, -1.0190e-02, -5.5602e-02,
-2.2949e-02, -1.6017e-02, -2.0295e-02, -6.1467e-03, -4.1679e-02,
-3.3808e-02, -1.5946e-02, 1.2528e-02, -1.7425e-03, 1.0002e-02,
1.3999e-03, -2.1473e-02, 2.9041e-02, 8.1162e-03, -3.6859e-03,
-2.8920e-02, -1.9641e-02, 4.9203e-02, 1.1021e-02, -1.3119e-02,
1.9755e-02, -3.8844e-02, -1.1669e-02, 3.3912e-02, 1.3763e-02,
-3.5422e-02, 2.3399e-03, -4.5410e-02, -5.0237e-02, -1.2711e-02,
6.7663e-03, -3.8081e-02, -4.7378e-02, 9.1057e-03, 9.7086e-03,
1.8040e-02, -1.2091e-02, 1.0468e-02, -1.0993e-02, 8.1390e-04,
-1.5350e-02, -5.2436e-02, -2.2084e-02, 5.2573e-03, -4.9846e-02,
3.6649e-03, -1.9814e-03, -3.5178e-02, 3.8680e-04, 1.6706e-03,
1.8115e-02, 1.4849e-03, 8.6505e-03, -2.5120e-02, 3.9394e-02,
-9.8747e-03, 2.3633e-02, -3.0123e-02, -9.2278e-03, 2.5567e-02,
-7.3859e-03, -1.4000e-02, 2.2307e-02, -2.9660e-02, 2.5312e-03,
1.6757e-02, -1.2032e-02, -6.9583e-03, -2.8649e-02, 9.3962e-03,
-6.9555e-02, -2.1766e-02, -1.2629e-02, -3.7239e-02, -3.6394e-02,
-1.8847e-02, 3.1566e-02, -4.9777e-02, -4.2465e-03, -2.7758e-02,
3.7707e-04, 8.1679e-02, -1.7641e-02, -9.5395e-03, -7.5895e-04,
-3.7009e-02, 1.7522e-03, -8.6521e-03, -3.1135e-02, 1.1772e-02,
2.9063e-02, 3.0317e-03, 2.3242e-02, 4.1135e-03, 2.4706e-03,
1.9642e-02, 4.5938e-03, -2.0781e-02, -2.3492e-02, -2.0666e-02,
5.8963e-02, 4.1321e-02, 1.2015e-02, -1.2244e-02, -3.4152e-02,得到了一个非常大的输出,但我们感兴趣的是每个图像的logits。为了获得概率,需要将这些logits传入softmax层。通过对每个logit的输出调用softmax来获得概率。
outputs.logits_per_imagetensor([[21.8763, 9.7856]], grad_fn=)
这样就获取logits的softmax,并取第一个元素,现在我们有了看起来像概率的东西。第一个元素是图像确实是占领者照片的概率,第二个是照片是猫照片的概率。
probs = outputs.logits_per_image.softmax(dim=1)[0]
probstensor([9.9999e-01, 5.6118e-06], grad_fn=)
最后,我们可以看到,对于标签"占领者的照片",概率几乎是100%,而对于第二个标签,概率接近于零
probs = list(probs)
for i in range(len(labels)):
print(f"label: {labels[i]} - probability of {probs[i].item():.4f}")label: a photo of occupiers --- probability of 1.0000 label: a photo of a cats --- probability of 0.0000
总结
本文详细介绍了如何使用CLIP模型实现零样本图像分类。零样本学习是计算机视觉领域的一项重大进展,它使AI系统能够对未经明确训练的类别进行分类。我们首先解释零样本学习和CLIP模型的基本概念,然后提供实际实现的详细步骤指南。
主要内容包括:环境设置、CLIP模型和处理器的加载、图像准备、自定义标签定义、模型输入构建,以及分类结果的处理和解释。我们重点强调了CLIP模型的灵活性和强大的跨模态学习能力,这使其能在各种视觉分类任务中表现卓越。
最后我们通过一个具体示例,演示如何使用CLIP模型对图像进行分类,并详细解释如何解读模型输出的概率。无论您是零样本学习的新手,还是寻找在实际项目中实现CLIP的参考,本文都能为你提供有价值的信息和指导。
https://avoid.overfit.cn/post/b88b5ce03e304aee87997c31ac80dc92
作者:Youssef Hosni