华为OD-D卷多段线数据压缩

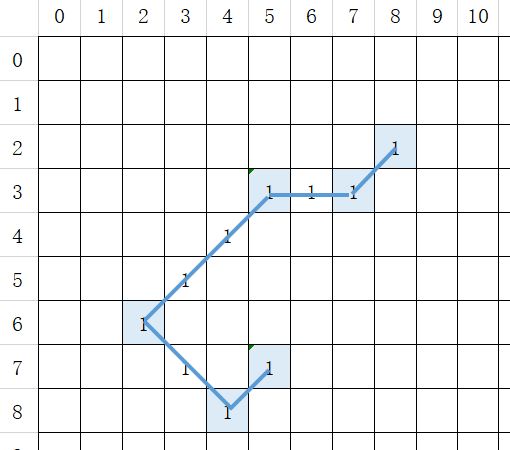
下图中，每个方块代表一个像素，每个像素用其行号和列号表示。

为简化处理，多段线的走向只能是水平、竖直、斜向45度。

上图中的多段线可以用下面的坐标串表示：(2, 8), (3, 7), (3, 6), (3, 5), (4, 4), (5, 3), (6, 2), (7, 3), (8, 4), (7, 5)。

但可以发现，这种表示不是最简的，其实只需要存储6个蓝色的关键点即可，它们是线段的起点、拐点、终点，而剩下4个点是冗余的。

现在，请根据输入的包含有冗余数据的多段线坐标列表，输出其最简化的结果。

输入描述:

2 8 3 7 3 6 3 5 4 4 5 3 6 2 7 3 8 4 7 5

1、所有数字以空格分隔，每两个数字一组，第一个数字是行号，第二个数字是列号；

2、行号和列号范围为[0,64)，用例输入保证不会越界，考生不必检查；

3、输入数据至少包含两个坐标点。

输出描述:

2 8 3 7 3 5 6 2 8 4 7 5

压缩后的最简化坐标列表，和输入数据的格式相同。

备注:

输出的坐标相对顺序不能变化。

题目解析：看似有点复杂，实际上每一步只有八种变化方式，上下左右，以及四个对角，可以通过两个变量分别记录当前变化的方式和上一步变化的方式，两次变化方式一致则可以缩减，剔除的是上一步的数据，但是取出的时候需要保持顺序不变，也就是前后都有操作，选择双端队列操作即可！

java 复制代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
//        int[] nums = new int[]{2, 8, 3, 7, 3, 6, 3, 5, 4, 4, 5, 3, 6, 2, 7, 3, 8, 4, 7, 5};
        Scanner scanner = new Scanner(System.in);
        String[] s = scanner.nextLine().split(" ");
        int[] nums = new int[s.length];
        for (int i = 0; i < nums.length; i++) {
            nums[i] = Integer.parseInt(s[i]);
        }
        Deque<Integer> x = new LinkedList<>();
        Deque<Integer> y = new LinkedList<>();
        // 题目中提到输入至少有两个数
        x.push(nums[0]);
        y.push(nums[1]);
        int type = 0;
        int frontType = 0;
        for (int i = 2; i < nums.length; i += 2) {
            int x1 = nums[i];
            int y1 = nums[i + 1];
            // 判断类型（可以再优化下这里）
            if (x1 - x.peekLast() == -1 && y1 - y.peekLast() == 0) {
                type = 1;
            } else if (x1 - x.peekLast() == 1 && y1 - y.peekLast() == 0) {
                type = 2;
            } else if (x1 - x.peekLast() == 0 && y1 - y.peekLast() == -1) {
                type = 3;
            } else if (x1 - x.peekLast() == -1 && y1 - y.peekLast() == -1) {
                type = 4;
            } else if (x1 - x.peekLast() == 1 && y1 - y.peekLast() == -1) {
                type = 5;
            } else if (x1 - x.peekLast() == 0 && y1 - y.peekLast() == 1) {
                type = 6;
            } else if (x1 - x.peekLast() == -1 && y1 - y.peekLast() == 1) {
                type = 7;
            } else if (x1 - x.peekLast() == 1 && y1 - y.peekLast() == 1) {
                type = 8;
            }
            if (frontType == 0 || frontType != type) {
                frontType = type;
            // 删除上一步位置
            } else if (frontType == type) {
                x.pollLast();
                y.pollLast();
            }
            // 放入当前位置
            x.add(nums[i]);
            y.add(nums[i + 1]);
        }
        // 注意输出最后没有空格
        while (x.size() > 1) {
            System.out.print(x.pollFirst() + " " + y.pollFirst() + " ");
        }
        System.out.println(x.pollFirst() + " " + y.pollFirst());
    }
}