傅里叶变换

傅里叶变换

对于周期信号，如果满足 \(Dirichlet\) 条件，就可以尝试将其分解为傅里叶级数，并绘制成频谱的形式，但是在实际使用的过程中我们遇到的信号往往既不是周期的信号又难以获取解析式。对于复杂的现实信号，我们可以将问题的难点拆分开，我们先解决不是周期信号但解析式已知的情况，再去解决难以获取解析式的情况。

从周期信号到非周期信号

首先我们先看一个问题：对于周期矩形脉冲信号，周期不断变大过程中，频谱如何发生变化？

经过实验我们得到下面的一组图：

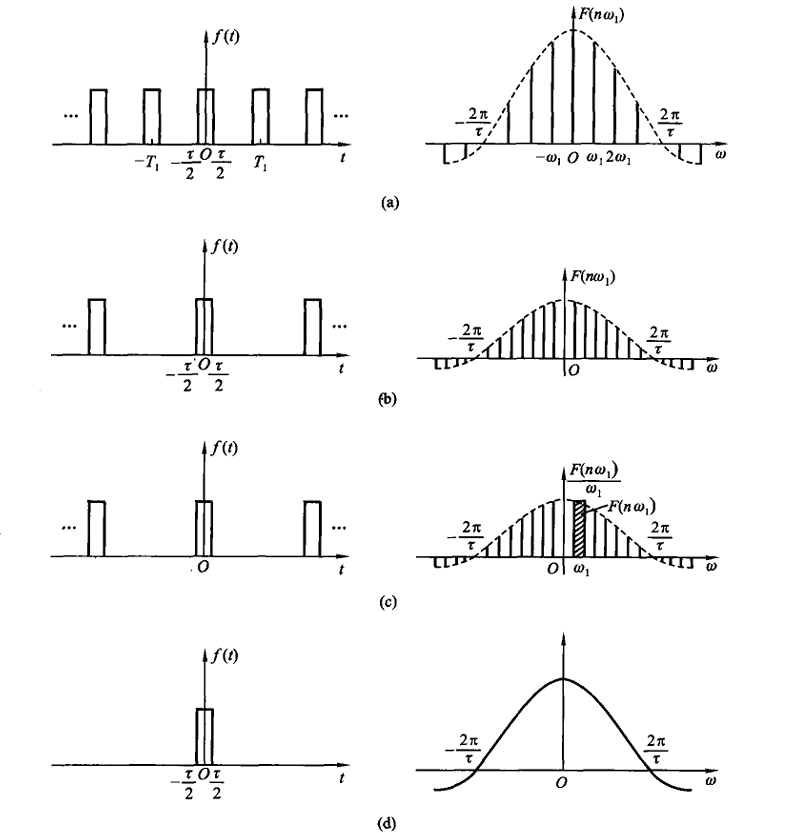
我们可以观察到，随着周期的不断变大，频谱的谱线之间距离变得越来越近。

上面的分析结果虽然是针对于周期矩形脉冲信号而言的，但是其具有一定的普适性，对于其他周期信号而言也能得到类似的结论。由此得到一个简单的想法------------非周期信号可以视作信号的周期为\(\infty\)的周期信号 。另外，我们知道信号的能量是有限值，对于周期信号，由帕斯瓦尔定理，我们知道幅度谱线的纵坐标的数值是与能量相关的参数，在改变信号周期的时候我们并未对其中的能量进行改变，也就是总的面积不变。基于这样的考虑，我们引入一个函数 "频谱密度函数"，函数中的每一个值都是在一个频率点附近能量和频率的比值，类似于概率论中概率密度函数中离散和连续的情况。

接下来就按照上述思想进行公式推导，看能否得到什么？

指数形式的傅里叶级数：

\[f(t) = \sum_{n = -\infty}^{\infty} F(n \omega )e^{j n \omega t} \\ \]

频谱为：

\[F(n \omega) = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{{-j n \omega t}} \text{{d}t }\\ \]

两边同时乘上周期或者说是除以频率：

\[F(n \omega) T= \frac{2\pi}{\omega} F(n \omega) = \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{{-j n \omega t}} \text{{d}t }\\ \]

当周期 \(T\to \infty\) ，有 \(\omega \to 0\) ，同时还有 \(n \to 1\) 。定义函数：

\[F(\omega) = \lim_{ \omega \to 0 } \frac{2\pi}{\omega} F(n \omega) = \lim_{ T \to \infty } F(n \omega) T \]

式子中 \(\displaystyle{\frac{2\pi F(n \omega)}{\omega}}\) 就是频谱密度，称 \(F(\omega)\) 为频谱密度函数，简称频谱函数。

由此我们便能够得到下面这样一组式子：

\[F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j \omega t}\text{d}x \]

\[f(t) = \frac{1}{2\pi} \int _{-\infty}^{\infty} F(\omega) e^{j \omega t} \, \text{d}x \]

上面的两个式子便是傅里叶变换公式和傅里叶反变换公式，并且称上面的\(f(t)\)和\(F(\omega)\)为一个傅里叶变换对，简记为\(f(t)\leftrightarrow F(\omega)\).

其中的 \(F(\omega)\) 是个复数，将他的模值 \(|F(\omega) |\) 作为幅度谱，相位作为相位谱。于是就得到了非周期信号的两谱图。

与周期信号离散的谱图类似，非周期信号的连续谱图中，幅度谱为偶函数，相位谱图为奇函数。

上面的推理过程在数学上并不是严格的，理论上傅里叶变化也不是任何函数都能进行变换，需要满足条件：

\[\int _{-\infty}^{\infty} | f(t)|\, \text{d}x < \infty \]

但是对于大多数信号都是满足上面的关系的，并且傅里叶变换是个很好的工具，对于某些奇异函数也是适用的（如冲激信号和阶跃信号等）。

典型非周期信号的傅里叶变换

（一）单边指数信号

原信号：

\[f(t) = \begin{cases} e^{-at} \qquad &(t \geqslant 0)\\ \\ 0 \qquad &(t < 0)\\ \end{cases} \]

傅里叶变换后的式子：

\[\begin{cases} F(\omega) = \displaystyle\frac{1}{a+j \omega}\\ \\ | F(\omega) | = \displaystyle{\frac{1}{\sqrt{a^{2} + \omega^{2}}}}\\ \\ \varphi(\omega) = -\arctan\left( \displaystyle\frac{\omega}{a} \right)\\ \end{cases} \]

（二）双边指数信号

双边指数信号：

\[f(t) = e^{-a | t |} \qquad (-\infty < t<\infty) \]

双边指数信号的傅里叶变换：

\[\begin{cases} F(\omega) = \displaystyle\frac{2a}{a^{2}+\omega^{2}}\\ \\ | F(\omega) | = \displaystyle{\frac{2a}{{a^{2} + \omega^{2}}}}\\ \\ \varphi(\omega) = 0\\ \end{cases} \]

（三）矩形脉冲信号

矩形脉冲信号：

\[f(t) = E\left[u\left( t - \displaystyle{\frac{\tau}{2}} \right) - u\left( t - \displaystyle{\frac{\tau}{2}} \right) \right] \]

矩形脉冲信号的傅里叶变换：

\[\begin{cases} F(\omega) = E\tau \cdot\text{Sa}\left( \displaystyle{\frac{\omega\tau}{2}} \right)\\ \\ |F(\omega)| = E\tau \cdot \left|\text{Sa}\left( \displaystyle{\frac{\omega\tau}{2}} \right)\right|\\ \\ \varphi(\omega) = \begin{cases}0\\ \pi\\ \end{cases} \end{cases} \]

（四）钟形脉冲信号

钟形信号：

\[f(t) = Ee^{- (\frac {t}{\tau})^{2}} \]

钟形信号的傅里叶变换：

\[F(\omega) =\sqrt{ \pi } E\tau \cdot e^{-(\frac{\omega \tau} {2})^{2}} \]

依旧是钟形的

（五）符号函数

符号函数：

\[f(t) = \text{sgn}(t) \]

符号函数本身不满足绝对可积分，但是可以对他进行傅里叶变换

不妨设想双边奇对称指数信号，如果 \(a\to 0\) 的话就非常的接近符号函数，对他进行傅里叶变换，就可以得到

符号函数的傅里叶变换：

\[\begin{cases} F(\omega) & = \displaystyle \frac{2}{j \omega}\\ \\ | F(\omega) | & = \displaystyle{ \frac{2}{| \omega |}}\\ \\ \varphi (\omega) & = \begin{cases} -\displaystyle \frac{\pi}{2}\quad & & (\omega > 0 )\\ \\ \displaystyle \frac{\pi}{2} \quad & & (\omega <0)\\ \end{cases} \end{cases} \]

（六）升余弦脉冲信号

升余弦脉冲信号：

\[f(t) = \frac{E}{2} \left[ 1 + \cos \left( \frac{\pi t}{\tau} \right) \right] \quad (0 \leqslant |t| \leqslant \tau) \]

就是把余弦信号向上平移半个峰峰值，第一个凸起的信号

升余弦信号的傅里叶变换

\[\begin{aligned} F(\omega) & = \frac {E\sin(\omega \tau)}{\omega \left[ 1 - \left(\frac{\omega \tau}{\pi}^{2}\right) \right]}\\ \\ & = \frac{E\tau\text{Sa}(\omega t)}{1 - \left(\frac{\omega \tau }{\pi}\right)^{2}} \end{aligned} \]

前面我们计算了一些常见的傅里叶变换，但是这样的计算更多是为了便于读者熟悉傅里叶变换这样的工具。当读者熟悉傅里叶变换的相关性质，上面的部分信号有更加简便的求解方式。下面我们继续学习一些奇异信号的傅里叶变换。

奇异信号的傅里叶变换

（一）冲激函数的傅里叶变换

冲激函数的傅里叶变换为：

\[\mathscr{F} \Big[\delta(t)\Big] = 1 \]

单位冲激函数的频谱为常数，或者说是"白色谱"。

冲激函数的傅里叶逆变换（从冲激函数的傅里叶变化可以推出）：

\[\mathscr{F}^{-1} \Big[ \delta(\omega)\Big]= \frac{1}{2\pi} \]

切记特殊信号的傅里叶逆变换直接进行积分运算可能较为复杂，如果不熟悉复变函数的积分会得到错误结论。 比如下面的。

\[\mathscr{F}(1) = 2\pi \delta(\omega) \]

直流信号的傅里叶变换是零点处的冲激信号。

（二）冲击偶函数的傅里叶变换

冲击偶函数的傅里叶变换可以通过下面方法得到：

\[\begin{aligned} & \delta(t) = \frac{1}{2\pi} \int _{-\infty}^{\infty} e^{j \omega t} \, \text{d}\omega \\ \\ & \quad (\text{对两边求导})\\ \\ & \frac{\text{d}}{\text{d}t} \delta(t) = \frac{1}{2\pi} \int _{-\infty}^{\infty} j \omega e^{j \omega t} \, \text{d}\omega \end{aligned} \]

由此可以知道冲激函数的傅里叶变换为：

\[\mathscr{F} \Big[ \frac{\text{d}}{\text{d}t} \delta(t) \Big] = j \omega \]

如果直接采用傅里叶变换的定义和冲击偶函数的性质也可以得到上面的结论。

同理可以知道：

\[\mathscr{F} \Big[ \frac{\text{d}^{n}}{\text{d}t^{n}} \delta(t) \Big] = (j \omega )^{n} \]

\[\mathscr{F} \Big[ t^{n} \Big] = 2\pi (j)^{n} \frac{\text{d}^{n}}{\text{d}\omega^{n}} \delta(\omega ) \]

（三）阶跃函数的傅里叶变换

\[\mathscr{F}\Big[u(t)\Big]= \pi \delta(\omega) + \frac{1}{j\omega} \]

傅里叶变换的性质

傅里叶变换的性质能够极大的简化某些复杂信号的计算过程，因此势必要仔细理解每一条性质并且活学活用。

（一）对称性

若 \(F(\omega) = \mathscr{F}\Big[ f(t)\Big]\) ，则 \(\mathscr{F}\Big[ F(t)\Big] = 2\pi f(-\omega)\) .

如果知道 \(f(t)\) ，我们需要求他的傅里叶变换后图形的傅里叶变换，则可以通过求解 \(2\pi f(-\omega)\) 得到。

（二）叠加性

先叠加再傅里叶变换等于先傅里叶变换再叠加。也就是傅里叶变换满足线性变换的性质。

（三）奇偶虚实性

1、\(f(t)\) 是实函数

实函数的傅里叶变换的实部为偶函数，虚部为奇函数，幅度谱为偶函数，相位谱为奇函数。

\[\begin{cases} R(\omega) = R(-\omega)\\ \\ X(\omega) = -X(-\omega)\\ \\ F(-\omega) = F^{*}(\omega)\\ \end{cases} \]

推论：实偶函数的傅里叶变换是实偶函数，实奇函数的傅里叶变换是虚奇函数。

2、\(f(t)\) 为虚函数

虚函数的傅里叶变换的实部为奇函数，虚部为偶函数。

\[\begin{cases} R(\omega) = R(-\omega)\\ \\ X(\omega) = -X(-\omega)\\ \\ F(-\omega) = F^{*}(\omega)\\ \end{cases} \]

3、\(f(t)\) 为实函数或者复函数

\[\begin{cases} \mathscr{F}\Big[ f(-t)\Big] = F(-\omega)\\ \\ \mathscr{F}\Big[ f^{*}(t)\Big] = F^{*}(-\omega)\\ \\ \mathscr{F}\Big[ f^{*}(-t)\Big] = F^{*}(\omega)\\ \end{cases} \]

（四）尺度变换特性

若 \(\mathscr{F}\Big[ f(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}\Big[ f(at)\Big] = \frac{1}{|a|}F\left( \frac{\omega}{a} \right) \]

时域上信号的压缩，等于频域上信号的扩展；

时域上信号的扩展，等于频域上信号的压缩。

关于 \(\displaystyle \frac{1}{|a|}\) 的物理含义：

时域上的压缩，信号能量减少，因此需要乘上 \(\displaystyle \frac{1}{|a|}, \quad(a>1)\) ；

时域上的扩展，信号能量变多，因此需要乘上 \(\displaystyle \frac{1}{|a|}, \quad(a<1)\) .

信号的等效脉宽与占有的等效带宽成反比例，要想获得更快的传输密度，需要压缩脉宽，同时需要占用更大的频带，是对频带资源的浪费。

（五）时移特性

若 \(\mathscr{F}\Big[ f(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}\Big[ f(t - t_{0})\Big] = e^{-j \omega t_{0}}F\left( \omega \right) \]

时间上的移动会导致频带上幅度谱的谱值不变，并且带来相位上 \(-\omega t_{0}\). 从这里可以知道时间上的滞后不会影响信号的能量.

（六）频移特性

若 \(\mathscr{F}\Big[ f(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}\left[ f(t) e^{j\omega_{0} t}\right] = F\left( \omega - \omega_{0}\right) \]

频移技术：将原信号乘上一个正弦、余弦或者正余弦混合信号，等效于乘上 \(e^{j \omega_{0} t}\) 随后就将信号的频谱进行了移动，使其移动到合适的未被占用的频带。这项技术广泛应用于通信中。

（七）微分特性

若 \(\mathscr{F}\Big[ f(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}\left[ \frac{\text{d}^{n}f(t)}{\text{d}t^{n}} \right] = (j\omega)^{n} F\left( \omega \right) \]

若 \(\mathscr{F}\Big[ F(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}^{-1} \left[ \frac{\text{d}^{n}F(\omega)}{\text{d}\omega^{n}} \right] = (-jt)^{n} f(t) \]

（八）积分特性

若 \(\mathscr{F}\Big[ f(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}\left[ \int_{-\infty}^{t} f(\tau) \text{d} \tau \right ] = \frac{F\left( \omega \right) }{j \omega} + \pi F(0) \delta(\omega) \]

若 \(\mathscr{F}\Big[ F(t)\Big] = F(\omega)\) , 则

\[\mathscr{F}^{-1} \left[ \int_{-\infty}^{\omega} F(\Omega) \text{d} \Omega \right] = - \frac{f(t)}{jt} + \pi f(0) \delta(t) \]

（九）卷积性质

1、时域卷积定理

给定两个时间函数 \(f_1(t)\) 和 \(f_2(t)\)

已知:

\[\begin{aligned} \mathscr{F}[f_{1}(t)] & = F_{1}(\omega)\\ \mathscr{F}[f_{2}(t)] & = F_{2}(\omega) \end{aligned} \]

则：

\[\mathscr{F}[f_{1}(t) * f_{2}(t)] = F_{1}(\omega) F_{2}(\omega) \]

两函数的卷积的傅里叶变换等于两函数傅里叶变换后的乘积。

2、频域卷积定理

给定两个时间函数 \(f_1(t)\) 和 \(f_2(t)\)

已知：

\[\begin{aligned} \mathscr{F}[f_{1}(t)] & = F_{1}(\omega)\\ \mathscr{F}[f_{2}(t)] & = F_{2}(\omega) \end{aligned} \]

则：

\[\mathscr{F}[f_{1}(t) \cdot f_{2}(t)] = \frac{1}{2\pi}F_{1}(\omega) * F_{2}(\omega) \]

两函数的傅里叶变换在频域上的卷积再乘上 \(\displaystyle{\frac{1}{2\pi}}\) 后的结果与两函数相乘后在进行傅里叶变换相同。

频域卷积定理主要用在通信系统的调制与解调。

结语

傅里叶变换是信号分析和通信的基础，后续的其他类型的傅里叶变换也是基于最原始的傅里叶变化得到的，无论是离散时间傅里叶变换还是离散傅里叶变换，都需要对原始的傅里叶变换非常熟悉。浅显描述傅里叶变换和傅里叶级数，傅里叶级数相当于把信号一巴掌拍散，出现无限个有一定间隔的幻影，而傅里叶变换将信号拍成致密幻影。

文章的最后附上一张傅里叶变换表，方便读者查阅。

性质	时域\(f(t)\)	频域\(F(\omega)\)	时域频域对应关系
1. 线性	\(\sum_{i=1}^{n}{a_{i}f_{i}(t)}\)	\(\sum_{i=1}^{n}{a_{i}F_{i}(\omega)}\)	线性叠加
2. 对称性	\(F(t)\)	\(2\pi f(-\omega)\)	对称
3. 尺度变换	\(f(at)\)	\(\frac{1}{| a |}F\left( \frac{\omega}{a} \right)\)	压缩与扩展
4. 时移	\(f(t-t_{0})\)	\(F(\omega)e^{-j\omega t_{0}}\)	时移与相移
5. 频移	\(f(t)e^{j\omega_{0}t}\)	\(F(\omega-\omega_{0})\)	调制与频移
6. 时域微分	\(\frac{\text{d}^{n}f(t)}{\text{d}t^{n}}\)	\((j\omega)^{n} F( \omega)\)
7. 频域微分	\((-jt)^{n} f(t)\)	\(\frac{\text{d}^{n}F(\omega)}{\text{d}\omega^{n}}\)
8. 时域积分	\(\int_{-\infty}^{t} f(\tau) \text{d} \tau\)	\(\frac{F\left( \omega \right) }{j \omega} + \pi F(0) \delta(\omega)\)
9. 时域卷积	\(f_{1}(t) * f_{2}(t)\)	\(F_{1}(\omega) F_{2}(\omega)\)
10. 频域卷积	\(f_{1}(t) \cdot f_{2}(t)\)	\(\frac{1}{2\pi}F_{1}(\omega) * F_{2}(\omega)\)