一、理论基础
参考:
dfs
dfs搜索可一个方向,并需要回溯,所以用递归的方式来实现是最方便的。
有递归的地方就有回溯,例如如下代码:
cpp
void dfs(参数) {
处理节点
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}可以看到回溯操作就在递归函数的下面,递归和回溯是相辅相成的。
在讲解二叉树章节的时候,二叉树的递归法其实就是dfs,而二叉树的迭代法,就是bfs(广度优先搜索)
所以dfs,bfs其实是基础搜索算法,也广泛应用与其他数据结构与算法中。
我们在回顾一下回溯法的代码框架:
cpp
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}回溯算法,其实就是dfs的过程,这里给出dfs的代码框架:
cpp
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}深搜三部曲
在 二叉树递归讲解中,给出了递归三部曲。
回溯算法讲解中,给出了 回溯三部曲。
其实深搜也是一样的,深搜三部曲如下:
1.确认递归函数,参数
cpp
void dfs(参数)通常我们递归的时候,我们递归搜索需要了解哪些参数,其实也可以在写递归函数的时候,发现需要什么参数,再去补充就可以。
一般情况,深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局变量,避免让我们的函数参数过多。
例如这样:
cpp
vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图,目前搜索的节点) 这种写法看个人习惯,不强求。
2.确认终止条件
终止条件很重要,很多同学写dfs的时候,之所以容易死循环,栈溢出等等这些问题,都是因为终止条件没有想清楚。
cpp
if (终止条件) {
存放结果;
return;
}终止添加不仅是结束本层递归,同时也是我们收获结果的时候。
3.处理目前搜索节点出发的路径
一般这里就是一个for循环的操作,去遍历 目前搜索节点 所能到的所有节点。
cpp
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}bfs
广搜的使用场景
广搜的搜索方式就适合于解决两个点之间的最短路径问题。
因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
当然,也有一些问题是广搜 和 深搜都可以解决的,例如岛屿问题,这类问题的特征就是不涉及具体的遍历方式,只要能把相邻且相同属性的节点标记上就行。
代码框架
bfs的代码使用的容器是什么?
其实,我们仅仅需要一个容器,能保存我们要遍历过的元素就可以,那么用队列,还是用栈,甚至用数组,都是可以的。
用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针。
因为队列是先进先出,加入元素和弹出元素的顺序是没有改变的。
如果用栈的话,就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈有顺时针遍历。
因为栈是先进后出,加入元素和弹出元素的顺序改变了。
用队列,还是用栈都是可以的,下面的讲解用队列,只不过要说清楚,并不是非要用队列,用栈也可以。
下面给出广搜代码模板,该模板针对的就是,上面的四方格的地图: (详细注释)
cpp
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图,也就是一个二维数组
// visited标记访问过的节点,不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que; // 定义队列
que.push({x, y}); // 起始节点加入队列
visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点
while(!que.empty()) { // 开始遍历队列里的元素
pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
int curx = cur.first;
int cury = cur.second; // 当前节点坐标
for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了,直接跳过
if (!visited[nextx][nexty]) { // 如果节点没被访问过
que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点
visited[nextx][nexty] = true; // 只要加入队列立刻标记,避免重复访问
}
}
}
}二、题目
1.797. 所有可能的路径(leetcode)
深搜 和 二叉树和回溯算法 有什么区别呢? 什么时候用深搜 什么时候用回溯?
我在讲解二叉树理论基础 (opens new window)的时候,提到过,二叉树的前中后序遍历其实就是深搜在二叉树这种数据结构上的应用。
那么回溯算法呢,其实 回溯算法就是 深搜,只不过针对某一搜索场景 我们给他一个更细分的定义,叫做回溯算法。
在二叉树遍历的单层逻辑中,处理的是所有孩子结点。
这就对应了图的深搜算法中"处理当前遍历到的节点的所有邻接点"
leetcode
leetcode中,本题给的参数是数据结构为邻接表的图,做好深搜三部曲:
(1)确定参数、返回值:
参数:邻接表、res、path设定为全局变量,dfs函数参数为当前遍历的结点。
不需要返回值
(2)返回条件
当前遍历的结点是终点节点时记录path,返回 (其他情况下最后到没有出度的结点也就自动回去了)
(3)单层处理逻辑
遍历当前节点的所有邻接点。
代码如下:
java
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> res = new ArrayList<>();
int[][] graph;
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
this.graph = graph;
//dfs
//参数:选择的结点
//返回条件:结点为n-1,或没有出度
path.add(0);
dfs(0);
return res;
}
public void dfs(int node){
if(node == graph.length-1){
res.add(new ArrayList<>(path));
return ;
}
for(int k = 0 ; k < graph[node].length ; k++){
path.add(graph[node][k]);
dfs(graph[node][k]);
path.remove(path.size()-1);
}
}
}kama
kama网要自定义图的结构,处理好输入输出:
图的存储
邻接矩阵
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
本题我们会有n 个节点,因为节点标号是从1开始的,为了节点标号和下标对齐,我们申请 n + 1 * n + 1 这么大的二维数组。
vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));输入m个边,构造方式如下:
cpp
while (m--) {
cin >> s >> t;
// 使用邻接矩阵 ,1 表示 节点s 指向 节点t
graph[s][t] = 1;
}邻接表
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
dfs
关于dfs函数的分析同leetcode
打印结果
ACM格式大家在输出结果的时候,要关注看看格式问题,特别是字符串,有的题目说的是每个元素后面都有空格,有的题目说的是 每个元素间有空格,最后一个元素没有空格。
有的题目呢,压根没说,那只能提交去试一试了。
邻接矩阵表示代码如下:
java
import java.util.*;
public class Main {
//邻接矩阵表示
static List<List<Integer>> res = new ArrayList<>();
static List<Integer> path = new ArrayList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] graph = new int[n+1][n+1];
for(int i = 0 ; i < m ; i++){
int node1 = scanner.nextInt();
int node2 = scanner.nextInt();
graph[node1][node2] = 1;
}
path.add(1);
dfs(graph,1);
//输出
if(res.isEmpty()){
System.out.println("-1");
}
for(List<Integer> list : res){
for(int i = 0 ; i < list.size() - 1 ; i++){
System.out.print(list.get(i) + " ");
}
System.out.println(list.get(list.size()-1));
}
}
public static void dfs(int[][] graph, int node){
if(node == graph.length - 1){
res.add(new ArrayList<>(path));
return;
}
for(int i = 1 ; i < graph[node].length ; i++){
if(graph[node][i] == 1){
path.add(i);
dfs(graph,i);
path.remove(path.size()-1);
}
}
}
}邻接表表示代码如下:
java
import java.util.*;
public class Main {
//邻接矩阵表示
static List<List<Integer>> res = new ArrayList<>();
static List<Integer> path = new ArrayList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
List<List<Integer>> graph = new ArrayList<>();
int n = scanner.nextInt();
int m = scanner.nextInt();
for(int i = 0 ; i <= n ; i++){
graph.add(new ArrayList<>());
}
for(int i = 0 ; i < m ; i++){
int node1 = scanner.nextInt();
int node2 = scanner.nextInt();
graph.get(node1).add(node2);
}
path.add(1);
dfs(graph,1,n);
//输出
if(res.isEmpty()){
System.out.println("-1");
}
for(List<Integer> list : res){
for(int i = 0 ; i < list.size() - 1 ; i++){
System.out.print(list.get(i) + " ");
}
System.out.println(list.get(list.size()-1));
}
}
public static void dfs(List<List<Integer>> graph, int node, int n){
if(node == n){
res.add(new ArrayList<>(path));
return ;
}
for(Integer nextNode : graph.get(node)){
path.add(nextNode);
dfs(graph,nextNode,n);
path.remove(path.size()-1);
}
}
}邻接表的表示方法中,存储graph的数据结构是List<List<Integer>>或 List<LinkedList<Integer>>都可以,比如:
java
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
public class Main {
static List<List<Integer>> result = new ArrayList<>(); // 收集符合条件的路径
static List<Integer> path = new ArrayList<>(); // 1节点到终点的路径
public static void dfs(List<LinkedList<Integer>> graph, int x, int n) {
if (x == n) { // 找到符合条件的一条路径
result.add(new ArrayList<>(path));
return;
}
for (int i : graph.get(x)) { // 找到 x指向的节点
path.add(i); // 遍历到的节点加入到路径中来
dfs(graph, i, n); // 进入下一层递归
path.remove(path.size() - 1); // 回溯,撤销本节点
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
// 节点编号从1到n,所以申请 n+1 这么大的数组
List<LinkedList<Integer>> graph = new ArrayList<>(n + 1);
for (int i = 0; i <= n; i++) {
graph.add(new LinkedList<>());
}
while (m-- > 0) {
int s = scanner.nextInt();
int t = scanner.nextInt();
// 使用邻接表表示 s -> t 是相连的
graph.get(s).add(t);
}
path.add(1); // 无论什么路径已经是从1节点出发
dfs(graph, 1, n); // 开始遍历
// 输出结果
if (result.isEmpty()) System.out.println(-1);
for (List<Integer> pa : result) {
for (int i = 0; i < pa.size() - 1; i++) {
System.out.print(pa.get(i) + " ");
}
System.out.println(pa.get(pa.size() - 1));
}
}
}对于这种有向图路径问题,最合适使用深搜。本题也可以使用广搜,但广搜相对来说就麻烦了一些,需要记录一下路径。
2.99. 岛屿数量
思路
注意题目中每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
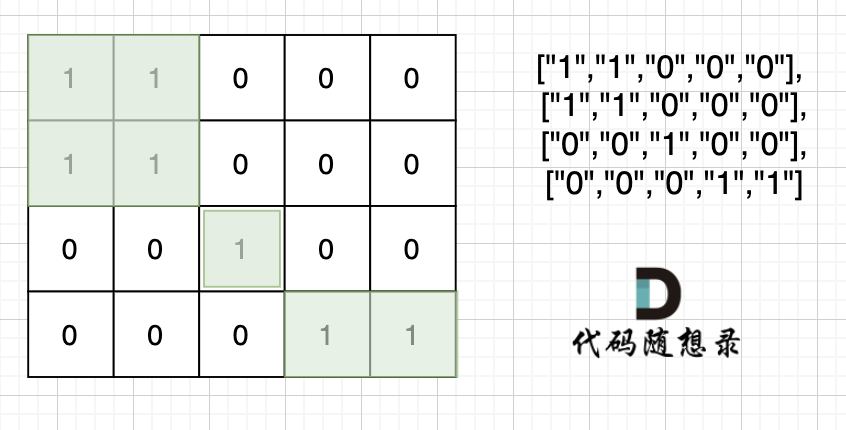
这道题题目是 DFS,BFS,并查集,基础题目。
本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
那么如何把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
dfs代码如下:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
int result = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 1 && visited[i][j] == false){
result++;
dfs(i,j,grid,visited);
}
}
}
System.out.println(result);
}
public static void dfs(int x, int y, int[][] grid, boolean[][] visited){
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if(grid[nextX][nextY] == 1 && visited[nextX][nextY] == false){
visited[nextX][nextY] = true;
dfs(nextX,nextY,grid,visited);
}
}
}
}在bfs中,使用队列作为容器。
不少同学用广搜做这道题目的时候,超时了。 这里有一个广搜中很重要的细节:
根本原因是只要 加入队列就代表 走过,就需要标记,而不是从队列拿出来的时候再去标记走过。
如果从队列拿出节点,再去标记这个节点走过,会导致很多节点重复加入队列。
比如:把A、B节点加入队列,但此时并没有标记A、B节点访问过,这时候访问A节点,A节点的邻接点有B节点,把B节点再次加入到了队列中,B节点重复加入队列。
bfs代码如下:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
int result = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 1 && visited[i][j] == false){
result++;
bfs(i,j,grid,visited);
}
}
}
System.out.println(result);
}
public static void bfs(int x, int y, int[][] grid, boolean[][] visited){
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{x,y});
visited[x][y] = true;
while(!queue.isEmpty()){
int[] point = queue.remove();
for(int i = 0 ; i < 4 ; i++) {
int nextX = point[0] + directions[i][0];
int nextY = point[1] + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if (visited[nextX][nextY] == false && grid[nextX][nextY] == 1) {
queue.add(new int[]{nextX, nextY});
visited[nextX][nextY] = true;
}
}
}
}
}3.100. 岛屿的最大面积
本题也是dfs和bfs的基础题目,搜索每个岛屿上"1"的数量,然后取一个最大的。
dfs实现:
dfs要注意对递归函数的设计。
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
static int cnt;
public static void main(String[] args) {
int result = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 1 && visited[i][j] == false){
cnt = 1;
visited[i][j] = true;
dfs(i,j,grid,visited);
result = Math.max(result,cnt);
}
}
}
System.out.println(result);
}
public static void dfs(int x, int y, int[][] grid, boolean[][] visited){
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if(visited[nextX][nextY] == false && grid[nextX][nextY] == 1){
cnt++;
visited[nextX][nextY] = true;
dfs(nextX,nextY,grid,visited);
}
}
}
}bfs实现:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
int maxArea = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 1 && visited[i][j] == false){
maxArea = Math.max(maxArea,bfs(i,j,grid,visited));
}
}
}
System.out.println(maxArea);
}
public static int bfs(int x, int y, int[][] grid, boolean[][] visited){
int area = 0;
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{x,y});
visited[x][y] = true;
area++;
while(!queue.isEmpty()){
int[] point = queue.remove();
for(int i = 0 ; i < 4 ; i++) {
int nextX = point[0] + directions[i][0];
int nextY = point[1] + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if (visited[nextX][nextY] == false && grid[nextX][nextY] == 1) {
queue.add(new int[]{nextX, nextY});
visited[nextX][nextY] = true;
area++;
}
}
}
return area;
}
}4.101. 孤岛的总面积
dfs和bfs思路同上,只是对结果的处理的不同。
思路1:统计所有岛的面积,不加入非孤岛的面积。需要多一个boolean标志位标志是否是孤岛。
dfs:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
static int cnt;
public static void main(String[] args) {
int result = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 1 && visited[i][j] == false){
cnt = 1;
visited[i][j] = true;
dfs(i,j,grid,visited);
result = Math.max(result,cnt);
}
}
}
System.out.println(result);
}
public static void dfs(int x, int y, int[][] grid, boolean[][] visited){
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if(visited[nextX][nextY] == false && grid[nextX][nextY] == 1){
cnt++;
visited[nextX][nextY] = true;
dfs(nextX,nextY,grid,visited);
}
}
}
}bfs实现如下:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
static boolean flag = false;
public static void main(String[] args) {
int totalArea = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 1 && visited[i][j] == false){
flag = true;
int tmp = bfs(i,j,grid,visited);
if(flag) totalArea += tmp;
}
}
}
System.out.println(totalArea);
}
public static int bfs(int x, int y, int[][] grid, boolean[][] visited){
if(x == 0 || y == 0 || x == grid.length - 1 || y == grid[0].length - 1) flag = false;
int area = 0;
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{x,y});
visited[x][y] = true;
area++;
while(!queue.isEmpty()){
int[] point = queue.remove();
if(point[0] == 0 || point[0] == grid.length -1 || point[1] == 0 || point[1] == grid[0].length -1) flag = false;
for(int i = 0 ; i < 4 ; i++) {
int nextX = point[0] + directions[i][0];
int nextY = point[1] + directions[i][1];
if(nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) continue;
if (visited[nextX][nextY] == false && grid[nextX][nextY] == 1) {
queue.add(new int[]{nextX, nextY});
visited[nextX][nextY] = true;
area++;
}
}
}
return area;
}
}思路2:先把所有的非陆地岛都标记为0,具体方法是对所有的边界进行遍历,如果边界是陆地,那么对该块进行bfs或dfs清0,最后累加所有的陆地面积。
dfs实现:
bfs实现:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
int totalArea = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
if(grid[i][0] == 1) dfs(i,0,grid,visited);
}
for(int j = 0 ; j < m ; j++){
if(grid[0][j] == 1) dfs(0,j,grid,visited);
}
for(int j = 0 ;j < m ; j++){
if(grid[n-1][j] == 1) dfs(n-1,j,grid,visited);
}
for(int i = 0 ; i < n ; i++){
if(grid[i][m-1] == 1) dfs(i,m-1,grid,visited);
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++) {
totalArea += grid[i][j];
}
}
System.out.println(totalArea);
}
public static void dfs(int x, int y, int[][] grid, boolean[][] visited){
grid[x][y] = 0;
visited[x][y] = true;
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX > grid.length - 1 || nextY < 0 || nextY > grid[0].length -1) continue;
if(grid[nextX][nextY] == 1 && visited[nextX][nextY] == false){
dfs(nextX,nextY,grid,visited);
}
}
}
}bfs实现:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
int totalArea = 0;
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
if(grid[i][0] == 1)bfs(i,0,grid,visited);
}
for(int j = 0 ; j < m ; j++){
if(grid[0][j] == 1) bfs(0,j,grid,visited);
}
for(int j = 0 ;j < m ; j++){
if(grid[n-1][j] == 1) bfs(n-1,j,grid,visited);
}
for(int i = 0 ; i < n ; i++){
if(grid[i][m-1] == 1) bfs(i,m-1,grid,visited);
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++) {
totalArea += grid[i][j];
}
}
System.out.println(totalArea);
}
public static void bfs(int x, int y, int[][] grid, boolean[][] visited){
grid[x][y] = 0;
visited[x][y] = true;
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{x,y});
while(!queue.isEmpty()){
int[] point = queue.remove();
for(int i = 0 ; i < 4 ; i++){
int nextX = point[0] + directions[i][0];
int nextY = point[1] + directions[i][1];
if(nextX < 0 || nextX > grid.length-1 || nextY < 0 || nextY > grid[0].length -1) continue;
if(grid[nextX][nextY] == 1 && visited[nextX][nextY] == false){
visited[nextX][nextY] = true;
grid[nextX][nextY] = 0;
queue.add(new int[]{nextX,nextY});
}
}
}
}
}5.102. 沉没孤岛
对每一个陆地,判断其是否是孤岛,是的话,对一开始那块陆地dfs或bfs,沉没孤岛。
这种需要两次判断,太麻烦了。
使用上一题的思路2,对岛屿中的非孤岛判定为2,最后遍历地图,2设为1,1设为0.
dfs实现:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
if(grid[i][0] == 1) dfs(i,0,grid,visited);
}
for(int j = 0 ; j < m ; j++){
if(grid[0][j] == 1) dfs(0,j,grid,visited);
}
for(int j = 0 ;j < m ; j++){
if(grid[n-1][j] == 1) dfs(n-1,j,grid,visited);
}
for(int i = 0 ; i < n ; i++){
if(grid[i][m-1] == 1) dfs(i,m-1,grid,visited);
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 2){
grid[i][j] =1;
}else if(grid[i][j] == 1){
grid[i][j] = 0;
}
}
}
for(int[] arr : grid){
for(int i = 0 ; i < arr.length -1 ; i++){
System.out.print(arr[i] + " ");
}
System.out.println(arr[arr.length-1]);
}
}
public static void dfs(int x, int y, int[][] grid, boolean[][] visited){
grid[x][y] = 2;
visited[x][y] = true;
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX > grid.length - 1 || nextY < 0 || nextY > grid[0].length -1) continue;
if(grid[nextX][nextY] == 1 && visited[nextX][nextY] == false){
dfs(nextX,nextY,grid,visited);
}
}
}
}bfs实现:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
boolean[][] visited = new boolean[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
for(int i = 0 ; i < n ; i++){
if(grid[i][0] == 1)bfs(i,0,grid,visited);
}
for(int j = 0 ; j < m ; j++){
if(grid[0][j] == 1) bfs(0,j,grid,visited);
}
for(int j = 0 ;j < m ; j++){
if(grid[n-1][j] == 1) bfs(n-1,j,grid,visited);
}
for(int i = 0 ; i < n ; i++){
if(grid[i][m-1] == 1) bfs(i,m-1,grid,visited);
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 2){
grid[i][j] =1;
}else if(grid[i][j] == 1){
grid[i][j] = 0;
}
}
}
for(int[] arr : grid){
for(int i = 0 ; i < arr.length -1 ; i++){
System.out.print(arr[i] + " ");
}
System.out.println(arr[arr.length-1]);
}
}
public static void bfs(int x, int y, int[][] grid, boolean[][] visited){
grid[x][y] = 2;
visited[x][y] = true;
Queue<int[]> queue = new ArrayDeque<>();
queue.add(new int[]{x,y});
while(!queue.isEmpty()){
int[] point = queue.remove();
for(int i = 0 ; i < 4 ; i++){
int nextX = point[0] + directions[i][0];
int nextY = point[1] + directions[i][1];
if(nextX < 0 || nextX > grid.length-1 || nextY < 0 || nextY > grid[0].length -1) continue;
if(grid[nextX][nextY] == 1 && visited[nextX][nextY] == false){
visited[nextX][nextY] = true;
grid[nextX][nextY] = 2;
queue.add(new int[]{nextX,nextY});
}
}
}
}
}6.103. 水流问题
本题的核心也是dfs和bfs,只是能够延伸的相邻节点的判断逻辑不同,逻辑为"相邻的、地势更低的点"。
思路
一个比较直白的想法,其实就是 遍历每个点,然后看这个点 能不能同时到达第一组边界和第二组边界。
至于遍历方式,可以用dfs,也可以用bfs。
实现代码如下:
cpp
#include <iostream>
#include <vector>
using namespace std;
int n, m;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
// 从 x,y 出发 把可以走的地方都标记上
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
if (grid[x][y] < grid[nextx][nexty]) continue; // 高度不合适
dfs (grid, visited, nextx, nexty);
}
return;
}
bool isResult(vector<vector<int>>& grid, int x, int y) {
vector<vector<bool>> visited(n, vector<bool>(m, false));
// 深搜,将x,y出发 能到的节点都标记上。
dfs(grid, visited, x, y);
bool isFirst = false;
bool isSecond = false;
// 以下就是判断x,y出发,是否到达第一组边界和第二组边界
// 第一边界的上边
for (int j = 0; j < m; j++) {
if (visited[0][j]) {
isFirst = true;
break;
}
}
// 第一边界的左边
for (int i = 0; i < n; i++) {
if (visited[i][0]) {
isFirst = true;
break;
}
}
// 第二边界右边
for (int j = 0; j < m; j++) {
if (visited[n - 1][j]) {
isSecond = true;
break;
}
}
// 第二边界下边
for (int i = 0; i < n; i++) {
if (visited[i][m - 1]) {
isSecond = true;
break;
}
}
if (isFirst && isSecond) return true;
return false;
}
int main() {
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 遍历每一个点,看是否能同时到达第一组边界和第二组边界
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (isResult(grid, i, j)) {
cout << i << " " << j << endl;
}
}
}
}这种思路很直白,但很明显,以上代码超时了。 来看看时间复杂度。
遍历每一个节点,是 m * n,遍历每一个节点的时候,都要做深搜,深搜的时间复杂度是: m * n
那么整体时间复杂度 就是 O(m^2 * n^2) ,这是一个四次方的时间复杂度。
优化
那么我们可以 反过来想,从第一组边界上的节点 逆流而上,将遍历过的节点都标记上。
同样从第二组边界的边上节点 逆流而上,将遍历过的节点也标记上。
然后两方都标记过的节点就是既可以流太平洋也可以流大西洋的节点。
从第一组边界边上节点出发,如图:
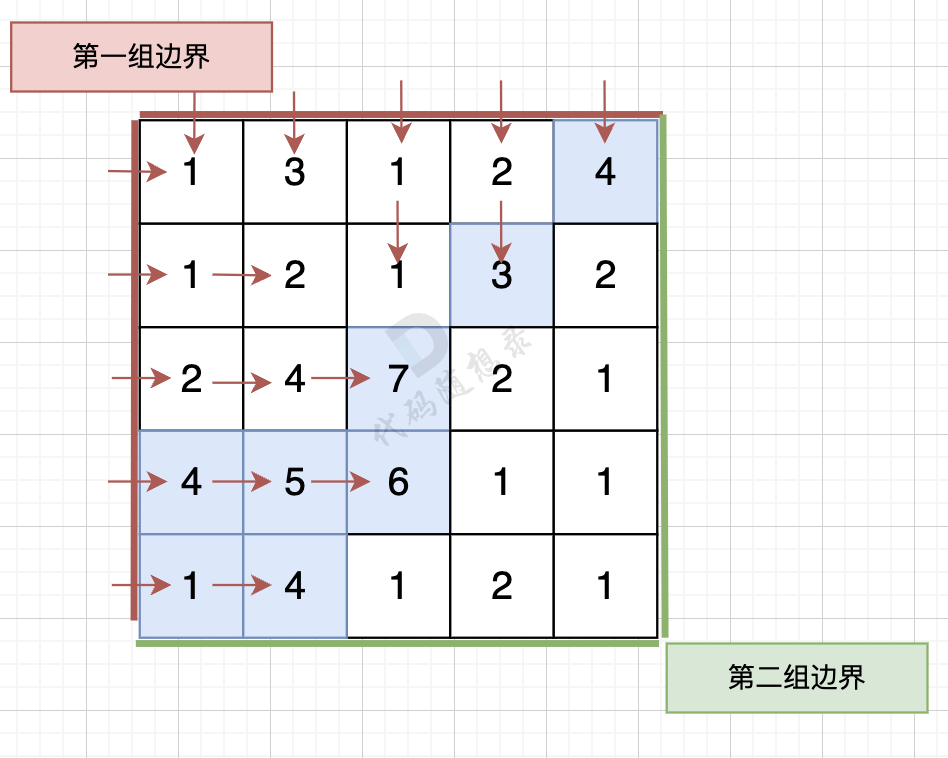
从第二组边界上节点出发,如图:
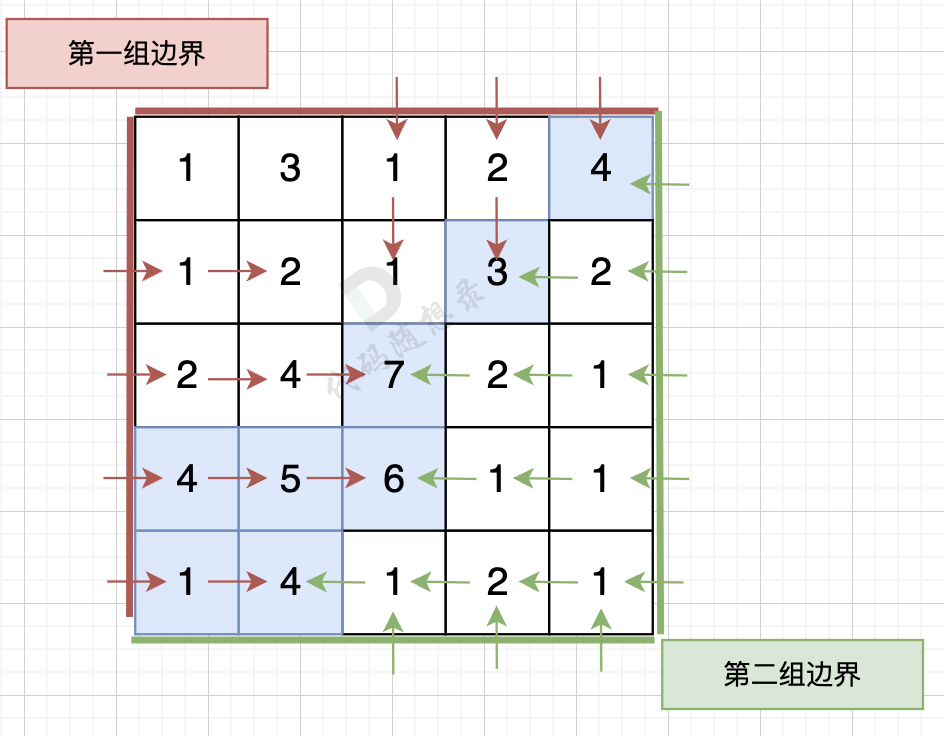
dfs代码如下:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
boolean[][] first = new boolean[n][m];
boolean[][] second = new boolean[n][m];
//第一边界
for(int j = 0 ; j < m ; j++){
first[0][j] = true;
dfs(0,j,grid,first);
}
for(int i = 0 ; i < n ; i++){
first[i][0] = true;
dfs(i,0,grid,first);
}
//第二边界
for(int i = 0 ; i < n ; i++){
second[i][m-1] = true;
dfs(i,m-1,grid,second);
}
for(int j = 0 ; j < m ; j++){
second[n-1][j] = true;
dfs(n-1,j,grid,second);
}
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(first[i][j] && second[i][j]){
System.out.println(i + " " + j);
}
}
}
}
public static void dfs(int x, int y , int[][] grid, boolean[][] visited){
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX > grid.length-1 || nextY < 0 || nextY > grid[0].length-1) continue;
if(grid[nextX][nextY] >= grid[x][y] && visited[nextX][nextY] == false){
visited[nextX][nextY] = true;
dfs(nextX,nextY,grid,visited);
}
}
}
}时间复杂度分析:由于visited数组的存在,两次逆流而上的时候,至多遍历整个图的结点,时间复杂度 2*n*m,答案输出部分 n*m
总的时间复杂度O(n*m)
7.104. 建造最大岛屿
思路
本题的一个暴力想法,应该是遍历地图尝试 将每一个 0 改成1,然后去搜索地图中的最大的岛屿面积。
优化思路
(1)用一次深搜把每一个岛屿的面积都记录下来,不同编号的岛屿mark不一样,用map做mark与对应面积的记录。
(2)遍历地图中的"0"(水),看水周围相邻的岛屿编号,得到对应的面积,遍历完一次得到最大的面积。
(1)的时间复杂度是n^2,(2)的时间复杂度也是n^2,最后总计的时间复杂度是O(n^2)
代码如下:
java
import java.util.*;
public class Main {
static int[][] directions= {{0,1},{1,0},{0,-1},{-1,0}};
static int cnt;
static int mark = 2;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
grid[i][j] = scanner.nextInt();
}
}
boolean[][] visited = new boolean[n][m];
//遍历地图,岛屿与对应面积编号储存进入map
Map<Integer,Integer> area = new HashMap<>();
boolean isAllLand = true;
Set<Integer> set = new HashSet<>();//存储答案的岛屿编号
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 0) isAllLand = false;
if(grid[i][j] == 0 || visited[i][j]) continue;
grid[i][j] = mark;
visited[i][j] = true;
cnt = 1;
dfs(i,j,grid,visited);
area.put(mark++,cnt);
}
}
//遍历map,对每个0的位置求答案,取最大的答案
int result = 0 ;
int tmpArea;
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(grid[i][j] == 0){
tmpArea = 0;
set.clear();
for(int k = 0 ; k < 4 ; k++){
int nextX = i + directions[k][0];
int nextY = j + directions[k][1];
if(nextX < 0 || nextX > grid.length-1 || nextY < 0 || nextY > grid[0].length-1)continue;
set.add(grid[nextX][nextY]);
}
for(Integer num : set){
tmpArea += area.getOrDefault(num,0);
}
result = Math.max(result,tmpArea + 1);//这个加的1是被填充的0
}
}
}
if(isAllLand) System.out.println(m*n);
else System.out.println(result);
}
public static void dfs(int x, int y , int[][] grid, boolean[][] visited){
for(int i = 0 ; i < 4 ; i++){
int nextX = x + directions[i][0];
int nextY = y + directions[i][1];
if(nextX < 0 || nextX > grid.length-1 || nextY < 0 || nextY > grid[0].length-1) continue;
if(grid[nextX][nextY] == 1 && visited[nextX][nextY] == false ){
visited[nextX][nextY] = true;
grid[nextX][nextY] = mark;
cnt++;
dfs(nextX,nextY,grid,visited);
}
}
}
}8.110. 字符串接龙
思路
以示例1为例,从这个图中可以看出 abc 到 def的路线 不止一条,但最短的一条路径上是4个节点。
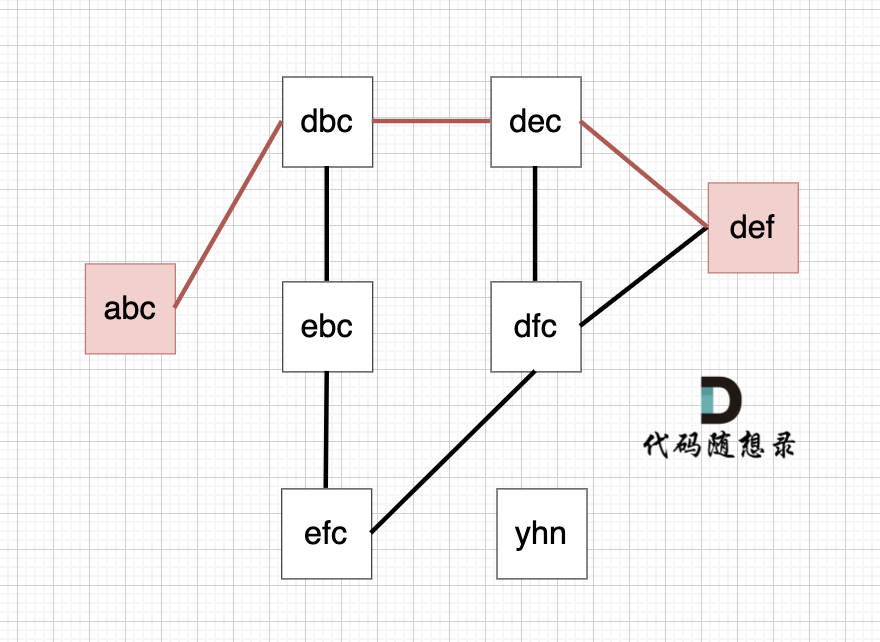
本题只需要求出最短路径的长度就可以了,不用找出具体路径。
所以这道题要解决两个问题:
- 图中的线是如何连在一起的(解决抽象成图的问题,关键问题也是邻接点的逻辑判断。之前的流水(从高到低)的问题也是修改临界点的逻辑判断。)
- 起点和终点的最短路径长度(bfs)
首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个。
所以判断点与点之间的关系,需要判断是不是差一个字符,如果差一个字符,那就是有链接。
然后就是求起点和终点的最短路径长度,这里无向图求最短路,广搜最为合适,广搜只要搜到了终点,那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜,会比较麻烦,要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点,一定是最短路。
另外需要有一个注意点:
- 本题是一个无向图,需要用标记位,标记着节点是否走过,否则就会死循环!
- 使用set来检查字符串是否出现在字符串集合里更快一些
代码如下:
java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
scanner.nextLine();
String[] strs = scanner.nextLine().split(" ");
List<String> wordList = new ArrayList<>();
for(int i = 0 ; i < n ; i++){
wordList.add(scanner.nextLine());
}
int result = bfs(strs[0],strs[1],wordList);
System.out.println(result);
}
public static int bfs(String beginStr, String endStr, List<String> wordList){
Map<String,Integer> map = new HashMap<>();
Set<String> set = new HashSet<>(wordList);
Queue<String> queue = new ArrayDeque<>();
queue.add(beginStr);
map.put(beginStr,1);
while(!queue.isEmpty()){
String str = queue.remove();
int path = map.get(str);
char[] charArray = str.toCharArray();
for(int i = 0; i < charArray.length ; i++){
for(char c = 'a' ; c <= 'z' ; c++){
charArray = str.toCharArray();
charArray[i] = c;
String newString = new String(charArray);
if(newString.equals(endStr)){
return path + 1;
}
if(set.contains(newString) && !map.containsKey(newString)){
map.put(newString,path + 1);
queue.add(newString);
}
}
}
}
return 0;
}
}先说一下核心部分,本题仍然是bfs的应用,只是判断邻接点的逻辑变成了"和原来的字符串相差1个字母",我们通过对原来字符串每个字母从a到z进行变换并查询是否在字典里,来去找它的邻接点。
再者,本题有很多细节要处理:
(1)读取完n后,输入流里还有换行符,因此此时要scanner.nextLine()读取一下剩下的换行符,否则在获取beginStr和endStr时不能得到想要的结果。
(2)Java里 == 是判断引用相等的方式,字符串内容相等用equals方法。
9.105.有向图的完全可达性
本题是一个有向图搜索全路径的问题。 只能用深搜(DFS)或者广搜(BFS)来搜。
深搜三部曲:
1.确认递归函数,参数
需要传入地图,需要知道当前我们拿到的key,以至于去下一个房间。
同时还需要一个数组,用来记录我们都走过了哪些房间,这样好知道最后有没有把所有房间都遍历的,可以定义一个一维数组。
所以 递归函数参数如下:
// key 当前得到的可以
// visited 记录访问过的房间
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {即:地图、当前遍历的结点、visited数组
2.确定终止条件
遍历的时候,什么时候终止呢?
这里有一个很重要的逻辑,就是在递归中,我们是处理当前访问的节点,还是处理下一个要访问的节点。
这决定 终止条件怎么写。
首先明确,本题中什么叫做处理,就是 visited数组来记录访问过的节点,该节点默认 数组里元素都是false,把元素标记为true就是处理 本节点了。
如果我们是处理当前访问的节点,当前访问的节点如果是 true ,说明是访问过的节点,那就终止本层递归,如果不是true,我们就把它赋值为true,因为这是我们处理本层递归的节点。
在这种情况下,本层逻辑无条件搜索所有本节点的邻接点,visited与否交由下一层判断。
代码就是这样:
cpp
// 写法一:处理当前访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
list<int> keys = graph[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(graph, key, visited);
}
}如果我们是处理下一层访问的节点,而不是当前层。那么就要在 深搜三部曲中第三步:处理目前搜索节点出发的路径的时候对 节点进行处理。
这样的话,就不需要终止条件(终止条件在本层的搜索逻辑里),而是在 搜索下一个节点的时候,直接判断 下一个节点是否是我们要搜的节点。
代码就是这样的:
cpp
// 写法二:处理下一个要访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
list<int> keys = graph[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(graph, key, visited);
}
}
}可以看出,如何看待 我们要访问的节点,直接决定了两种不一样的写法。
3.处理目前搜索节点出发的路径(本层逻辑)
这里还有细节:
看上面两个版本的写法中, 好像没有发现回溯的逻辑。
我们都知道,有递归就有回溯,回溯就在递归函数的下面, 那么之前我们做的dfs题目,都需要回溯操作,例如:0098.所有可达路径, 为什么本题就没有回溯呢?
代码中可以看到dfs函数下面并没有回溯的操作。
此时就要在思考本题的要求了,本题是需要判断 1节点 是否能到所有节点,那么我们就没有必要回溯去撤销操作了,只要遍历过的节点一律都标记上。
那什么时候需要回溯操作呢?
当我们需要搜索一条可行路径的时候,就需要回溯操作了,因为没有回溯,就没法"调头", 如果不理解的话,去看 0098.所有可达路径 的题解。
代码如下:
java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
List<List<Integer>> graph = new ArrayList<>();
for(int i = 0; i <= n ; i++){
graph.add(new ArrayList<>());
}
for(int i = 0 ; i < k ; i++){
int from = scanner.nextInt();
int to = scanner.nextInt();
graph.get(from).add(to);
}
boolean[] visited = new boolean[n+1];
visited[1] = true;
dfs(graph,1,visited);
for(int i = 1 ; i <= n ; i++){
if(!visited[i]){
System.out.println("-1");
return;
}
}
System.out.println("1");
}
public static void dfs(List<List<Integer>> graph, int node , boolean[] visited){
for(Integer nextNode : graph.get(node)){
if(!visited[nextNode]){
visited[nextNode] = true;
dfs(graph,nextNode,visited);
}
}
}
}10.106. 岛屿的周长
思路
岛屿问题最容易让人想到BFS或者DFS,但本题确实还用不上。
为了避免大家惯性思维,所以给大家安排了这道题目。
这道题思路像是遍历图的模拟题。
解法一:
遍历每一个空格,遇到岛屿则计算其上下左右的空格情况。
如果该陆地上下左右的空格是有水域,则说明是一条边,如图:
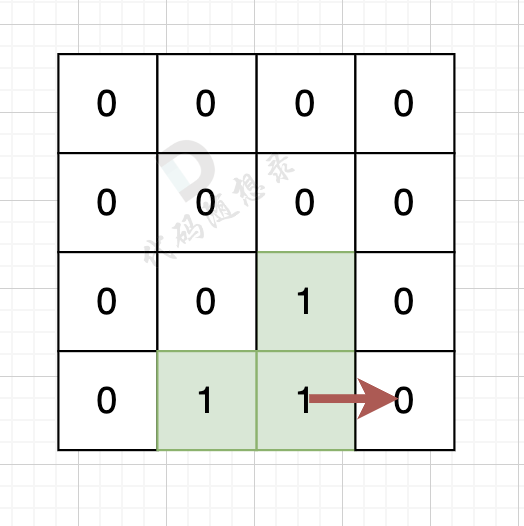
陆地的右边空格是水域,则说明找到一条边。
如果该陆地上下左右的空格出界了,则说明是一条边,如图:
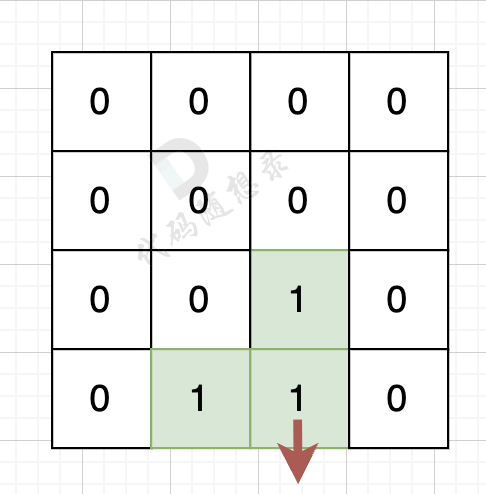
该陆地的下边空格出界了,则说明找到一条边。
解法二:
与解法一类似,反过来,对所有水域求周围情况,如果是陆地,则周长+1;再对所有边界遍历,如果是陆地,则周长+1;
代码如下:
java
import java.util.*;
public class Main {
static int[][] directions = {{1,0},{0,1},{-1,0},{0,-1}};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] graph = new int[n][m];
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
graph[i][j] = scanner.nextInt();
}
}
int perimeter = 0;
for(int i = 0 ; i < n ; i++){
for(int j = 0 ; j < m ; j++){
if(graph[i][j] == 1) continue;
for(int k = 0 ; k < 4 ; k++){
int nextX = i + directions[k][0];
int nextY = j + directions[k][1];
if(nextX < 0 || nextX > graph.length -1 || nextY < 0 || nextY > graph[0].length -1) continue;
if(graph[nextX][nextY] == 1) perimeter++;
}
}
}
//上边界
for(int j = 0 ; j < m ; j++){
if(graph[0][j] == 1) perimeter++;
}
//右边界
for(int i = 0 ; i < n ; i++){
if(graph[i][m-1] == 1) perimeter++;
}
//下边界
for(int j = 0 ; j < m ; j++){
if(graph[n-1][j] == 1) perimeter++;
}
//左边界
for(int i = 0 ; i < n ; i++){
if(graph[i][0] == 1) perimeter++;
}
System.out.println(perimeter);
}
}解法三:
本题中只有1个岛屿,可以得出一些数学性质:
计算出总的岛屿数量,总的变数为:岛屿数量 * 4
因为有一对相邻两个陆地,边的总数就要减2,如图红线部分,有两个陆地相邻,总边数就要减2
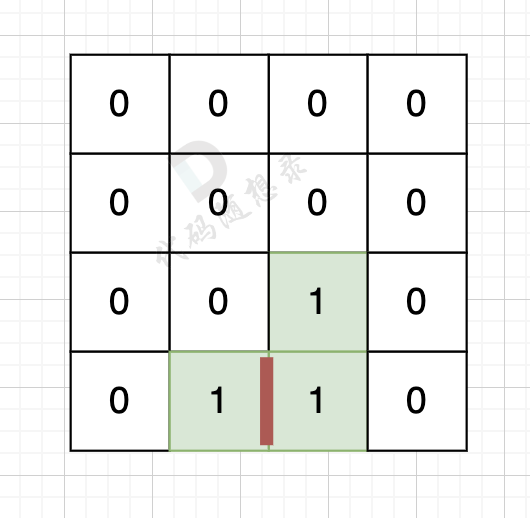
那么只需要在计算出相邻岛屿的数量就可以了,相邻岛屿数量为cover。
结果 result = 岛屿数量 * 4 - cover * 2;
C++代码如下:(详细注释)
cpp
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
int sum = 0; // 陆地数量
int cover = 0; // 相邻数量
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
sum++; // 统计总的陆地数量
// 统计上边相邻陆地
if(i - 1 >= 0 && grid[i - 1][j] == 1) cover++;
// 统计左边相邻陆地
if(j - 1 >= 0 && grid[i][j - 1] == 1) cover++;
// 为什么没统计下边和右边? 因为避免重复计算
}
}
}
cout << sum * 4 - cover * 2 << endl;
}这里计算相邻岛屿数量cover的时候,需要注意单向计算,遍历的时候只计算上边和左边,可以保证全部计算完毕并且不重复计算。