深度马尔可夫模型¶
介绍¶
我们将为序列数据建立一个深度概率模型:深度马尔可夫模型。我们想要建模的特定数据集由复调音乐片段组成。序列中的每个时间片跨越一个四分音符,由一个88维的二进制向量表示,该向量在该时间步长对音符进行编码。
由于音乐(显然)在时间上是一致的,我们需要一个模型来表示观察到的数据中复杂的时间相关性。例如,考虑这样一种模型是不合适的,在这种模型中,特定时间步的音符独立于先前时间步的音符。一种方法是建立一个潜在变量模型,其中观测值的可变性和时间结构由潜在变量的动态控制。
这个想法的一个具体实现是马尔可夫模型,其中我们有一个潜在变量链,链中的每个潜在变量都取决于前一个潜在变量。这是一种强大的方法,但是如果我们想要用复杂的(在这种情况下是未知的)动态来表示复杂的数据,我们希望我们的模型足够灵活,以适应潜在的高度非线性的动态。因此,深度马尔可夫模型:我们允许控制潜在变量动态的转移概率以及控制潜在动态如何产生观察的发射概率由(非线性)神经网络参数化。
我们将要实现的特定模型基于以下参考:
1\] `Structured Inference Networks for Nonlinear State Space Models`拉胡尔·克里希南、尤里·沙利特、戴维·桑塔格 请注意,虽然我们并不假设本教程的读者已经阅读了参考资料,但它绝对是在其他时间序列模型的上下文中寻找更全面的深度马尔可夫模型讨论的好地方。 我们已经描述了这个模型,但是我们如何去训练它呢?我们将要使用的推理策略是变分推理,它需要指定一个参数化的分布族,可以用来逼近潜在随机变量的后验分布。鉴于我们的模型和数据中固有的非线性和复杂的时间依赖性,我们期望精确的后验概率非常重要。所以如果我们希望学习一个好的模型,我们需要一个灵活的变分分布族。令人高兴的是,PyTorch和Pyro一起提供了所有必要的成分。正如我们将看到的,组装它们将是简单的。我们开始工作吧。 > [https://stackoverflow.com/questions/57710588/understanding-deep-markov-model-code-on-pyro](https://stackoverflow.com/questions/57710588/understanding-deep-markov-model-code-on-pyro "https://stackoverflow.com/questions/57710588/understanding-deep-markov-model-code-on-pyro")stackoverflow.com/questions/57710588/understanding-deep-markov-model-code-on-pyro > > 我正在浏览pyro网站上给出的一个深度马尔可夫模型代码: > > [Deep Markov Model --- Pyro Tutorials 1.9.1 documentation](https://pyro.ai/examples/dmm.html "Deep Markov Model — Pyro Tutorials 1.9.1 documentation") > > 我真的对他们实现的合并器模块感到困惑。您可以在GitHub页面的第104行找到合并器模块: > > [https://github . com/pyro-ppl/pyro/blob/dev/examples/DMM/DMM . py](https://github.com/pyro-ppl/pyro/blob/dev/examples/dmm/dmm.py "https://github . com/pyro-ppl/pyro/blob/dev/examples/DMM/DMM . py") > > 他们关注的文章是: > > [https://arxiv.org/abs/1609.09869](https://arxiv.org/abs/1609.09869 "https://arxiv.org/abs/1609.09869") > > 他们在第4节(结构化推理网络)中解释了组合器模块。我真的很困惑,为什么他们要在GitHub上从104行开始的代码中做三次线性变换。他们不是应该用RNN来制作发行版吗?还是我漏掉了什么?如有真知灼见,不胜感激。 > > ======================================= > > 回答 > > 1 这Combiner模块实施对应于第4页底部描述的公式,"结构化近似的组合函数(DKS)"。mu_t是loc而sigma_t\*\*2是scale. RNN状态用于参数化分布,但是该分布由两个变量参数化。这些变量是通过上述变换从RNN状态中提取出来的 ### **模型[¶](https://pyro.ai/examples/dmm.html#The-Model "¶")** 描述模型的高层结构的一个方便的方法是用图形模型。  **图1**:该模型推出T=3个时间步。 这里,我们推出了模型,假设观察序列的长度为3:{x1,x2,x3}。为了反映观察结果的顺序,我们还有一系列潜在的随机变量:{z1,z2,z3}。该图对模型的结构进行了编码。相应的联合分布是 p(x123,z123)=p(x1\|z1)p(x2\|z2)p(x3\|z3)p(z1)p(z2\|z1)p(z3\|z2) 以...为条件zt,每次观察xt与其他观测无关。这可以从以下事实中读出xt只取决于相应的潜伏zt如向下箭头所示。我们也可以读出模型的马尔可夫特性:每个潜在的zt,当以先前的潜伏为条件时zt−1独立于所有以前的延迟{zt−2,zt−3,...}。这有效地说明了人们需要知道的关于系统当时状态的一切t被潜在的zt. 我们将假设观察可能性,即概率分布p(xt\|zt)由伯努利分布给出。这是一个合适的选择,因为我们的观察值都是0或1。对于概率分布p(zt\|zt−1)控制潜在的动态,我们选择(条件)高斯分布与对角协方差。这是合理的,因为我们假设潜在空间是连续的。 实心黑色正方形表示由神经网络参数化的非线性函数。这就是为什么这是一个*深的*马尔可夫模型。请注意,黑色方块出现在两个不同的地方:在成对的潜伏之间,以及在潜伏和观察之间。连接潜在变量的非线性函数(图1中的"Trans ")控制潜在变量的动态。因为我们允许条件概率分布zt依赖于zt−1以一种复杂的方式,我们将能够在我们的模型中捕捉复杂的动态。类似地,将潜在变量连接到观察值的非线性函数(图1中的'Emit ')控制观察值如何依赖于潜在动力学。 一些附加说明:-我们可以自由选择潜在空间的维度以适应手头的问题:简单问题的小潜在空间和复杂动力学问题的大潜在空间-注意参数z0在图1中。从代码中可以看出,这只是我们参数化概率分布的一种便捷方式p(z1)对于第一个时间步长,没有先前的等待时间作为条件。 #### **门控跃迁和发射极[¶](https://pyro.ai/examples/dmm.html#The-Gated-Transition-and-the-Emitter "¶")** 事不宜迟,让我们开始写一些代码。我们首先定义两个PyTorch模块,它们对应于图1中的黑色方块。首先是发射函数: ``` class Emitter(nn.Module): """ Parameterizes the bernoulli observation likelihood p(x_t \| z_t) """ def __init__(self, input_dim, z_dim, emission_dim): super().__init__() # initialize the three linear transformations used in the neural network self.lin_z_to_hidden = nn.Linear(z_dim, emission_dim) self.lin_hidden_to_hidden = nn.Linear(emission_dim, emission_dim) self.lin_hidden_to_input = nn.Linear(emission_dim, input_dim) # initialize the two non-linearities used in the neural network self.relu = nn.ReLU() self.sigmoid = nn.Sigmoid() def forward(self, z_t): """ Given the latent z at a particular time step t we return the vector of probabilities \`ps\` that parameterizes the bernoulli distribution p(x_t\|z_t) """ h1 = self.relu(self.lin_z_to_hidden(z_t)) h2 = self.relu(self.lin_hidden_to_hidden(h1)) ps = self.sigmoid(self.lin_hidden_to_input(h2)) return ps ``` 在构造函数中,我们定义了将在发射函数中使用的线性变换。注意到`emission_dim`是神经网络中隐藏单元的数量。我们还定义了我们将使用的非线性。forward调用定义了函数的计算流程。我们接纳潜伏的人zt作为输入,进行一系列的变换,直到我们得到一个长度为88的向量,它定义了我们的伯努利似然的发射概率。因为乙状结肠,每个元素`ps`将介于0和1之间,并将定义一个有效的概率。综合了...的元素`ps`对我们期望观察到的音符进行编码t给定系统的状态(编码在zt). 现在我们定义门控转换函数: ``` class GatedTransition(nn.Module): """ Parameterizes the gaussian latent transition probability p(z_t \| z_{t-1}) See section 5 in the reference for comparison. """ def __init__(self, z_dim, transition_dim): super().__init__() # initialize the six linear transformations used in the neural network self.lin_gate_z_to_hidden = nn.Linear(z_dim, transition_dim) self.lin_gate_hidden_to_z = nn.Linear(transition_dim, z_dim) self.lin_proposed_mean_z_to_hidden = nn.Linear(z_dim, transition_dim) self.lin_proposed_mean_hidden_to_z = nn.Linear(transition_dim, z_dim) self.lin_sig = nn.Linear(z_dim, z_dim) self.lin_z_to_loc = nn.Linear(z_dim, z_dim) # modify the default initialization of lin_z_to_loc # so that it's starts out as the identity function self.lin_z_to_loc.weight.data = torch.eye(z_dim) self.lin_z_to_loc.bias.data = torch.zeros(z_dim) # initialize the three non-linearities used in the neural network self.relu = nn.ReLU() self.sigmoid = nn.Sigmoid() self.softplus = nn.Softplus() def forward(self, z_t_1): """ Given the latent z_{t-1} corresponding to the time step t-1 we return the mean and scale vectors that parameterize the (diagonal) gaussian distribution p(z_t \| z_{t-1}) """ # compute the gating function _gate = self.relu(self.lin_gate_z_to_hidden(z_t_1)) gate = self.sigmoid(self.lin_gate_hidden_to_z(_gate)) # compute the 'proposed mean' _proposed_mean = self.relu(self.lin_proposed_mean_z_to_hidden(z_t_1)) proposed_mean = self.lin_proposed_mean_hidden_to_z(_proposed_mean) # assemble the actual mean used to sample z_t, which mixes # a linear transformation of z_{t-1} with the proposed mean # modulated by the gating function loc = (1 - gate) * self.lin_z_to_loc(z_t_1) + gate * proposed_mean # compute the scale used to sample z_t, using the proposed # mean from above as input. the softplus ensures that scale is positive scale = self.softplus(self.lin_sig(self.relu(proposed_mean))) # return loc, scale which can be fed into Normal return loc, scale ``` 这反映了的结构`Emitter`以上,不同的是计算流程有点复杂。这有两个原因。第一,输出`GatedTransition`需要定义有效的(对角)高斯分布。所以我们需要输出两个参数:平均值`loc`,以及(平方根)协方差`scale`。这两者都需要具有与潜在空间相同的尺寸。第二,我们不想*力* 动力学是非线性的。因此我们的意思是`loc`是两项之和,其中只有一项非线性地依赖于输入`z_t_1`。这样,我们可以支持线性和非线性动态(或者实际上,潜在空间的一部分的动态是线性的,而其余的动态是非线性的)。 #### **模型-一个热随机函数[¶](https://pyro.ai/examples/dmm.html#Model---a-Pyro-Stochastic-Function "¶")** 到目前为止,我们所做的一切都是徒劳的。为了完成将我们的模型翻译成代码,我们需要引入Pyro。基本上,我们需要实现图1中的随机节点(即圆圈)。为此,我们引入了一个可调用的`model()`包含火焰元素的`pyro.sample`。这`sample`语句将用于指定潜在客户的联合分布z1:T。此外,在`obs`参数可以与`sample`语句来指定如何观察x1:T取决于latents。在我们看完整的代码之前`model()`,让我们来看一个包含主要逻辑的精简版本: ``` def model(...): z_prev = self.z_0 # sample the latents z and observed x's one time step at a time for t in range(1, T_max + 1): # the next two lines of code sample z_t \~ p(z_t \| z_{t-1}). # first compute the parameters of the diagonal gaussian # distribution p(z_t \| z_{t-1}) z_loc, z_scale = self.trans(z_prev) # then sample z_t according to dist.Normal(z_loc, z_scale) z_t = pyro.sample("z_%d" % t, dist.Normal(z_loc, z_scale)) # compute the probabilities that parameterize the bernoulli likelihood emission_probs_t = self.emitter(z_t) # the next statement instructs pyro to observe x_t according to the # bernoulli distribution p(x_t\|z_t) pyro.sample("obs_x_%d" % t, dist.Bernoulli(emission_probs_t), obs=mini_batch[:, t - 1, :]) # the latent sampled at this time step will be conditioned upon # in the next time step so keep track of it z_prev = z_t ``` 我们需要做的第一件事是取样z1。一旦我们取样z1,我们可以取样z2∼p(z2\|z1)诸如此类。这是在中实现的逻辑`for`循环。参数`z_loc`和`z_scale`定义了概率分布p(zt\|zt−1)计算方法如下`self.trans`,它只是`GatedTransition`上面定义的模块。第一次踏上t=1我们的条件是`self.z_0`,这是一个(可训练的)`Parameter`,而对于随后的时间步骤,我们以先前绘制的潜在值为条件。请注意,每个随机变量`z_t`由用户分配一个唯一的名称。 一旦我们取样zt在给定的时间步长,我们需要观察数据点xt。所以我们通过了`z_t`穿过`self.emitter`的一个实例`Emitter`上面定义的模块,以获得`emission_probs_t`。和论点一起`dist.Bernoulli()`在......里`sample`语句,这些概率完全指定了观察可能性。最后,我们还指定了观察数据的切片xt: `mini_batch[:, t - 1, :]`使用`obs`对...的争论`sample`. 这完全指定了我们的模型,并将它封装在一个可以传递给Pyro的callable中。在我们继续之前,让我们看一下的完整版本`model()`回顾一下我们在第一遍中忽略的一些细节。 ``` def model(self, mini_batch, mini_batch_reversed, mini_batch_mask, mini_batch_seq_lengths, annealing_factor=1.0): # this is the number of time steps we need to process in the mini-batch T_max = mini_batch.size(1) # register all PyTorch (sub)modules with pyro # this needs to happen in both the model and guide pyro.module("dmm", self) # set z_prev = z_0 to setup the recursive conditioning in p(z_t \| z_{t-1}) z_prev = self.z_0.expand(mini_batch.size(0), self.z_0.size(0)) # we enclose all the sample statements in the model in a plate. # this marks that each datapoint is conditionally independent of the others with pyro.plate("z_minibatch", len(mini_batch)): # sample the latents z and observed x's one time step at a time for t in range(1, T_max + 1): # the next chunk of code samples z_t \~ p(z_t \| z_{t-1}) # note that (both here and elsewhere) we use poutine.scale to take care # of KL annealing. we use the mask() method to deal with raggedness # in the observed data (i.e. different sequences in the mini-batch # have different lengths) # first compute the parameters of the diagonal gaussian # distribution p(z_t \| z_{t-1}) z_loc, z_scale = self.trans(z_prev) # then sample z_t according to dist.Normal(z_loc, z_scale). # note that we use the reshape method so that the univariate # Normal distribution is treated as a multivariate Normal # distribution with a diagonal covariance. with poutine.scale(None, annealing_factor): z_t = pyro.sample("z_%d" % t, dist.Normal(z_loc, z_scale) .mask(mini_batch_mask[:, t - 1:t]) .to_event(1)) # compute the probabilities that parameterize the bernoulli likelihood emission_probs_t = self.emitter(z_t) # the next statement instructs pyro to observe x_t according to the # bernoulli distribution p(x_t\|z_t) pyro.sample("obs_x_%d" % t, dist.Bernoulli(emission_probs_t) .mask(mini_batch_mask[:, t - 1:t]) .to_event(1), obs=mini_batch[:, t - 1, :]) # the latent sampled at this time step will be conditioned upon # in the next time step so keep track of it z_prev = z_t ``` 首先要注意的是`model()`需要一些参数。现在让我们来看看`mini_batch`和`mini_batch_mask`. `mini_batch`是一个三维张量,第一维是批量维度,第二维是时间维度,最后一个维度是特征(在我们的例子中是88维)。为了加速代码,无论何时我们运行`model`我们将处理整个小批量的序列(即,我们将利用矢量化)。 这是明智的,因为我们的模型是在单个观察序列上隐式定义的。一组序列的概率是由单个序列概率的乘积给出的。换句话说,给定模型的参数,序列是条件独立的。 这种矢量化带来了一些复杂性,因为序列可能有不同的长度。这是哪里`mini_batch_mask`进来了。`mini_batch_mask`是一个二维0/1维度的遮罩`mini_batch_size` x `T_max`,在哪里`T_max`是小批量中任何序列的最大长度。这编码了`mini_batch`是有效的观察。 所以我们要做的第一件事就是`T_max`:我们必须展开我们的模型至少这么多时间步。请注意,这将导致大量"浪费的"计算,因为一些序列会比`T_max`但是这对于矢量化带来的巨大速度提升来说只是一个小小的代价。我们只需要确保没有"浪费的"计算"污染"我们的模型计算。我们通过传递适合时间步长的掩码来实现这一点t到`mask`方法(作用于需要屏蔽的分布)。 最后一行`pyro.module("dmm", self)`相当于一堆`pyro.param`模型中每个参数的语句。这让Pyro知道哪些参数是模型的一部分。就像`sample`语句中,我们给模块一个唯一的名称。此名称将合并到的名称中`Parameters`在模型中。我们把KL退火因子的讨论留到以后。 ### **推理[¶](https://pyro.ai/examples/dmm.html#Inference "¶")** 至此,我们已经完全指定了我们的模型。下一步是让我们自己进行推理。正如在引言中提到的,我们的推理策略将是变分推理(参见[SVI第一部分](https://pyro.ai/examples/svi_part_i.html "SVI第一部分")用于介绍)。因此,我们的下一个任务是建立一个适合在深度马尔可夫模型中进行推理的变分分布族。然而,在这一点上值得强调的是,我们实现的方式`model()`把我们和变分推理联系起来。原则上我们可以使用*任何的*Pyro中可用的推理策略。例如,在这个特定的上下文中,人们可以想象使用顺序蒙特卡罗的一些变体(尽管这在Pyro中目前不被支持)。 #### **向导[¶](https://pyro.ai/examples/dmm.html#Guide "¶")** 指南(即变分分布)的目的是提供精确后验概率的(参数化)近似值p(z1:T\|x1:T)。实际上,这里有一个隐含的假设,我们应该把它明确化,所以让我们后退一步。假设我们的数据集D包括N顺序{x1:T11,x1:T22,...,x1:TNN}。那么我们真正感兴趣的后验概率由下式给出p(z1:T11,z1:T22,...,z1:TNN\|D),也就是说,我们想要推断*全部* N序列。即使是小的N这是一个非常高维的分布,需要大量的参数来指定。特别是,如果我们以这种形式直接参数化后验概率,所需参数的数量将(至少)线性增长N。避免数据集规模急剧增长的一种方法是*分期偿还* (参见中的类似讨论[SVI第二部分](https://pyro.ai/examples/svi_part_ii.html "SVI第二部分")). ##### **旁白:摊销[¶](https://pyro.ai/examples/dmm.html#Aside:-Amortization "¶")** 其工作原理如下。我们将学习一个单一的参数函数,而不是为数据集中的每个序列引入不同的参数f(x1:T)并处理具有以下形式的变分分布∏n=1Nq(z1:Tnn\|f(x1:Tnn))。该功能f(⋅)它基本上将一个给定的观察序列映射到一组为该序列定制的变化参数,需要足够丰富以准确捕捉后验,但现在我们可以处理大型数据集,而不必引入大量的变化参数。 所以我们的任务是构造函数f(⋅)。因为在我们的例子中,我们需要支持可变长度的序列,所以很自然f(⋅)让RNN参与进来。在我们看构成我们的各种组件之前f(⋅)具体来说,我们来看一个计算图,它对基本结构进行了编码:  **图2**:该指南推出了T=3个时间步长。 在图的底部,我们有我们的三个观察序列。这些观察值将被RNN消耗,它从右向左读取观察值并输出三个隐藏状态{h1,h2,h3}。请注意,这个计算已经完成*以前* 我们对任何潜在变量进行采样。接下来,每个隐藏状态都将被输入到一个`Combiner`其工作是输出条件分布的均值和协方差的模块q(zt\|zt−1,xt:T),我们认为它是由对角高斯分布给出的。(就像在模型中一样,条件结构的z1:T在指南中是这样的,我们样本zt向前看。)除了RNN潜州之外`Combiner`还将前一时间步的潜在随机变量作为输入,除了t=1,取而代之的是可训练(可变)参数z0q. ##### **旁白:导向结构[¶](https://pyro.ai/examples/dmm.html#Aside:-Guide-Structure "¶")** 为什么我们要设置RNN从右向左进行观察?为什么不是从左往右?有了这个选择,我们的条件分布q(zt\|...)取决于两件事: * 潜伏zt−1从前一时间步开始;和 * 观察结果xt:T,即当前观察值和所有未来观察值 我们可以自由地做出其他选择;所有需要的是,该指南是一个适当的规范化发行版,可以很好地播放签名。这种特殊的选择是由真实后验概率的依赖结构决定的:详细讨论见参考文献\[1\]。简而言之,虽然我们可以,例如,以整个观察序列为条件,但是由于模型的马尔可夫结构,我们需要知道关于先前观察的一切x1:t−1由封装zt−1。我们可以有更多的条件,但是没有必要;这样做可能会冲淡学习信号。因此,从右向左运行RNN是这种特定模型最自然的选择。 让我们来详细看看组成部分。首先是`Combiner`模块: ``` class Combiner(nn.Module): """ Parameterizes q(z_t \| z_{t-1}, x_{t:T}), which is the basic building block of the guide (i.e. the variational distribution). The dependence on x_{t:T} is through the hidden state of the RNN (see the pytorch module \`rnn\` below) """ def __init__(self, z_dim, rnn_dim): super().__init__() # initialize the three linear transformations used in the neural network self.lin_z_to_hidden = nn.Linear(z_dim, rnn_dim) self.lin_hidden_to_loc = nn.Linear(rnn_dim, z_dim) self.lin_hidden_to_scale = nn.Linear(rnn_dim, z_dim) # initialize the two non-linearities used in the neural network self.tanh = nn.Tanh() self.softplus = nn.Softplus() def forward(self, z_t_1, h_rnn): """ Given the latent z at at a particular time step t-1 as well as the hidden state of the RNN h(x_{t:T}) we return the mean and scale vectors that parameterize the (diagonal) gaussian distribution q(z_t \| z_{t-1}, x_{t:T}) """ # combine the rnn hidden state with a transformed version of z_t_1 h_combined = 0.5 * (self.tanh(self.lin_z_to_hidden(z_t_1)) + h_rnn) # use the combined hidden state to compute the mean used to sample z_t loc = self.lin_hidden_to_loc(h_combined) # use the combined hidden state to compute the scale used to sample z_t scale = self.softplus(self.lin_hidden_to_scale(h_combined)) # return loc, scale which can be fed into Normal return loc, scale ``` 该模块具有与相同的一般结构`Emitter`和`GatedTransition`在模型中。唯一值得注意的是,因为`Combiner`需要在每个时间步消耗两个输入,它将输入转换成一个组合的隐藏状态`h_combined`在它计算输出之前。 除了RNN,我们现在已经拥有了构建指南发行版所需的所有组件。幸运的是,PyTorch有很好的内置RNN模块,所以我们在这里没有太多工作要做。稍后我们将看到在哪里实例化RNN。让我们直接进入随机函数的定义`guide()`. ``` def guide(self, mini_batch, mini_batch_reversed, mini_batch_mask, mini_batch_seq_lengths, annealing_factor=1.0): # this is the number of time steps we need to process in the mini-batch T_max = mini_batch.size(1) # register all PyTorch (sub)modules with pyro pyro.module("dmm", self) # if on gpu we need the fully broadcast view of the rnn initial state # to be in contiguous gpu memory h_0_contig = self.h_0.expand(1, mini_batch.size(0), self.rnn.hidden_size).contiguous() # push the observed x's through the rnn; # rnn_output contains the hidden state at each time step rnn_output, _ = self.rnn(mini_batch_reversed, h_0_contig) # reverse the time-ordering in the hidden state and un-pack it rnn_output = poly.pad_and_reverse(rnn_output, mini_batch_seq_lengths) # set z_prev = z_q_0 to setup the recursive conditioning in q(z_t \|...) z_prev = self.z_q_0.expand(mini_batch.size(0), self.z_q_0.size(0)) # we enclose all the sample statements in the guide in a plate. # this marks that each datapoint is conditionally independent of the others. with pyro.plate("z_minibatch", len(mini_batch)): # sample the latents z one time step at a time for t in range(1, T_max + 1): # the next two lines assemble the distribution q(z_t \| z_{t-1}, x_{t:T}) z_loc, z_scale = self.combiner(z_prev, rnn_output[:, t - 1, :]) z_dist = dist.Normal(z_loc, z_scale) # sample z_t from the distribution z_dist with pyro.poutine.scale(None, annealing_factor): z_t = pyro.sample("z_%d" % t, z_dist.mask(mini_batch_mask[:, t - 1:t]) .to_event(1)) # the latent sampled at this time step will be conditioned # upon in the next time step so keep track of it z_prev = z_t ``` 的高层结构`guide()`非常类似于`model()`。首先注意模型和向导采用相同的参数:这是Pyro中模型/向导对的一般要求。在模型中,有一个调用`pyro.module`向Pyro注册所有参数。此外,在`for`循环的结构与`model()`,不同之处在于指南只需对潜在客户进行抽样(没有`sample`语句`obs`关键词)。最后,请注意指南中潜在变量的名称与模型中的名称完全匹配。这就是Pyro知道如何正确排列随机变量的方法。 PyTorch用户应该熟悉RNN逻辑,但是让我们快速浏览一遍。首先我们准备RNN的初始状态,`h_0`。然后我们通过它的前向调用调用RNN;产生的张量`rnn_output`包含整个小批量的隐藏状态。请注意,因为我们希望RNN从右向左使用观测值,所以RNN的输入为`mini_batch_reversed`,这是的副本`mini_batch`随着所有序列的运行*反面的* 时间顺序。此外,`mini_batch_reversed`被包裹在PyTorch里`rnn.pack_padded_sequence`以便RNN可以处理可变长度的序列。因为我们在潜在空间中以正常的时间顺序进行采样,所以我们使用辅助函数`pad_and_reverse`反转中的隐藏状态序列`rnn_output`,这样我们就可以养活`Combiner`RNN隐藏了正确排列和排序的状态。这个帮助器函数还解包`rnn_output`因此它不再是PyTorch的形式`rnn.pack_padded_sequence`. ### **将模型和指南打包为PyTorch模块[¶](https://pyro.ai/examples/dmm.html#Packaging-the-Model-and-Guide-as-a-PyTorch-Module "¶")** 在这个节骨眼上,我们准备进行推论。但是在此之前,让我们快速回顾一下我们是如何将模型和指南打包成一个PyTorch模块的。这通常是很好的做法,尤其是对于较大的模型。 ``` class DMM(nn.Module): """ This PyTorch Module encapsulates the model as well as the variational distribution (the guide) for the Deep Markov Model """ def __init__(self, input_dim=88, z_dim=100, emission_dim=100, transition_dim=200, rnn_dim=600, rnn_dropout_rate=0.0, num_iafs=0, iaf_dim=50, use_cuda=False): super().__init__() # instantiate pytorch modules used in the model and guide below self.emitter = Emitter(input_dim, z_dim, emission_dim) self.trans = GatedTransition(z_dim, transition_dim) self.combiner = Combiner(z_dim, rnn_dim) self.rnn = nn.RNN(input_size=input_dim, hidden_size=rnn_dim, nonlinearity='relu', batch_first=True, bidirectional=False, num_layers=1, dropout=rnn_dropout_rate) # define a (trainable) parameters z_0 and z_q_0 that help define # the probability distributions p(z_1) and q(z_1) # (since for t = 1 there are no previous latents to condition on) self.z_0 = nn.Parameter(torch.zeros(z_dim)) self.z_q_0 = nn.Parameter(torch.zeros(z_dim)) # define a (trainable) parameter for the initial hidden state of the rnn self.h_0 = nn.Parameter(torch.zeros(1, 1, rnn_dim)) self.use_cuda = use_cuda # if on gpu cuda-ize all pytorch (sub)modules if use_cuda: self.cuda() # the model p(x_{1:T} \| z_{1:T}) p(z_{1:T}) def model(...): # ... as above ... # the guide q(z_{1:T} \| x_{1:T}) (i.e. the variational distribution) def guide(...): # ... as above ... ``` 因为我们已经检查过了`model`和`guide`,我们这里的重点是构造函数。首先,我们实例化我们在模型和指南中使用的四个PyTorch模块。在模型方面:`Emitter`和`GatedTransition`。在导轨侧:`Combiner`和RNN。 接下来我们定义PyTorch`Parameter`s代表RNN的初始状态`z_0`和`z_q_0`,它们被输入到`self.trans`和`self.combiner`,代替不存在的随机变量z0. 这里要强调的重点是,所有这些`Module`s和`Parameter`是的属性`DMM`(它本身继承自`nn.Module`).这导致它们都被自动注册为属于该模块。例如,当我们打电话时`parameters()`在...的情况下`DMM`PyTorch将知道返回所有相关参数。这也意味着当我们调用`pyro.module("dmm", self)`在`model()`和`guide()`,模型和导轨的所有参数都将在Pyro中注册。最后,这意味着如果我们在GPU上运行,对`cuda()`会将所有参数移入GPU内存。 ### **随机变分推理[¶](https://pyro.ai/examples/dmm.html#Stochastic-Variational-Inference "¶")** 有了模型和指南,我们终于可以进行推理了。在我们看一个完整的实验脚本所涉及的全部逻辑之前,让我们先看看如何进行一个单独的梯度步骤。首先我们实例化一个`DMM`设置一个优化器。 ``` # instantiate the dmm dmm = DMM(input_dim, z_dim, emission_dim, transition_dim, rnn_dim, args.rnn_dropout_rate, args.num_iafs, args.iaf_dim, args.cuda) # setup optimizer adam_params = {"lr": args.learning_rate, "betas": (args.beta1, args.beta2), "clip_norm": args.clip_norm, "lrd": args.lr_decay, "weight_decay": args.weight_decay} optimizer = ClippedAdam(adam_params) ``` 这里我们使用的是Adam优化器的一个实现,它包括渐变裁剪。这减轻了在训练递归神经网络时可能出现的一些问题(例如,消失/爆炸梯度)。接下来,我们设置推理算法。 ``` # setup inference algorithm svi = SVI(dmm.model, dmm.guide, optimizer, Trace_ELBO()) ``` 推理算法`SVI`使用随机梯度估计器对目标函数采取梯度步骤,在这种情况下,目标函数由ELBO(证据下限)给出。顾名思义,ELBO是日志证据的下限:原木p(D)。当我们采取梯度步骤最大化ELBO时,我们移动我们的向导q(⋅)更靠近背部。 论点`Trace_ELBO()`构建一个版本的梯度估计器,它不需要访问模型和指南的依赖结构。因为我们模型中的所有潜在变量都是可重新参数化的,所以这是适合我们用例的梯度估计量。(也是默认选项。) 假设我们已经准备好了各种论点`dmm.model`和`dmm.guide`,采取梯度步骤是通过调用 ``` svi.step(mini_batch, ...) ``` 这就是全部了! 不完全是。这将是我们推理算法中的主要步骤,但是我们仍然需要实现一个完整的训练循环,包括准备小批量、评估等等。这种逻辑对任何深度学习者来说都是熟悉的,但是让我们看看它在PyTorch/Pyro中是怎样的。 ### **优化的魔力[¶](https://pyro.ai/examples/dmm.html#The-Black-Magic-of-Optimization "¶")** 实际上,在我们开始训练之前,让我们花点时间思考一下我们设置的优化问题。我们已经在一个具有高维潜在空间的非线性模型中交换了贝叶斯推理------一个困难的问题------一个特定的优化问题。别自欺欺人了,这个优化问题也很难。为什么?让我们来看看一些原因: * 我们正在优化的参数空间是非常高维的(它包括我们定义的所有神经网络中的所有权重)。 * 我们的目标函数(ELBO)不能用解析方法计算。因此,我们的参数更新将遵循噪声蒙特卡罗梯度估计 * 数据二次采样是随机性的一个额外来源:即使我们想这样做,我们通常也不能在整个数据集上定义的ELBO上采取梯度步骤(实际上在我们的特殊情况下,数据集并不是很大,但我们可以忽略它)。 * 考虑到回路中所有的神经网络和非线性,我们的(随机)损失面是非平凡的 结论是,如果我们要找到ELBO的合理(局部)最优解,我们最好在决定如何进行优化时多加小心。这不是讨论一个人可能采用的所有不同策略的时间或地点,但强调学习超参数(学习速率、小批量大小等)的好或坏的选择有多么决定性是很重要的。)可以。 在我们继续之前,让我们更详细地讨论我们正在使用的一个特定的优化策略:KL退火。在我们的情况下,ELBO是两项之和:预期对数似然项(测量模型拟合度)和KL散度项之和(用于调整近似后验概率): ELBO=Eq(z1:T)\[原木p(x1:T\|z1:T)\]−Eq(z1:T)\[原木q(z1:T)−原木p(z1:T)
后一项可能是一个非常强的正则项,在训练的早期阶段,它倾向于支持包含许多坏的局部最优值的损失曲面区域。参考文献[1]中也采用了避免这些不良局部最优的一种策略,即通过将KL散度项乘以一个标量来退火KL散度项annealing_factor范围在0到1之间:
Eq(z1:T)[原木p(x1:T|z1:T)]−annealing_factor×Eq(z1:T)[原木q(z1:T)−原木p(z1:T)]
这个想法是在训练的过程中annealing_factor从初始值(接近零)缓慢上升到最终值(1.0)。退火程序是任意的;下面我们将使用一个简单的线性时间表。就代码而言,为了通过适当的退火因子来调整对数似然性,我们将每个潜在的示例语句都包含在模型中,并用pyro.poutine.scale语境。
最后,我们应该提到,这里描述的DMM实现与参考文献[1]中使用的DMM实现之间的主要区别在于,它们利用了两个高斯分布之间的KL散度的解析公式(而我们依赖于蒙特卡罗估计)。这使得ELBO的方差梯度估计值更低,从而使训练变得更加容易。我们仍然可以在不进行这种分析替换的情况下训练模型,但是训练可能需要更长的时间,因为方差更大。要使用解析KL偏差,请使用TraceMeanField_ELBO.
数据加载、培训和评估¶
首先我们加载数据。训练数据集中有229个序列,每个序列的平均长度约为60个时间步长。
jsb_file_loc = "./data/jsb_processed.pkl"
data = pickle.load(open(jsb_file_loc, "rb"))
training_seq_lengths = data['train']['sequence_lengths']
training_data_sequences = data['train']['sequences']
test_seq_lengths = data['test']['sequence_lengths']
test_data_sequences = data['test']['sequences']
val_seq_lengths = data['valid']['sequence_lengths']
val_data_sequences = data['valid']['sequences']
N_train_data = len(training_seq_lengths)
N_train_time_slices = np.sum(training_seq_lengths)
N_mini_batches = int(N_train_data / args.mini_batch_size +
int(N_train_data % args.mini_batch_size > 0))对于这个数据集,我们通常使用mini_batch_size20,因此每个时期将有12个小批量。接下来我们定义函数process_minibatch其准备用于训练的小批量并采取梯度步骤:
def process_minibatch(epoch, which_mini_batch, shuffled_indices):
if args.annealing_epochs > 0 and epoch < args.annealing_epochs:
# compute the KL annealing factor appropriate
# for the current mini-batch in the current epoch
min_af = args.minimum_annealing_factor
annealing_factor = min_af + (1.0 - min_af) * \
(float(which_mini_batch + epoch * N_mini_batches + 1) /
float(args.annealing_epochs * N_mini_batches))
else:
# by default the KL annealing factor is unity
annealing_factor = 1.0
# compute which sequences in the training set we should grab
mini_batch_start = (which_mini_batch * args.mini_batch_size)
mini_batch_end = np.min([(which_mini_batch + 1) * args.mini_batch_size,
N_train_data])
mini_batch_indices = shuffled_indices[mini_batch_start:mini_batch_end]
# grab the fully prepped mini-batch using the helper function in the data loader
mini_batch, mini_batch_reversed, mini_batch_mask, mini_batch_seq_lengths \
= poly.get_mini_batch(mini_batch_indices, training_data_sequences,
training_seq_lengths, cuda=args.cuda)
# do an actual gradient step
loss = svi.step(mini_batch, mini_batch_reversed, mini_batch_mask,
mini_batch_seq_lengths, annealing_factor)
# keep track of the training loss
return loss我们首先计算适合于小批量的KL退火因子(根据前面描述的线性时间表)。然后,我们计算小批量索引,并将其传递给助手函数get_mini_batch。这个助手函数负责许多不同的事情:
-
它根据序列长度对每个小批量进行排序
-
它调用另一个助手函数来以相反的时间顺序获得小批量的副本
-
它将每个反转的小批量包装在一个
rnn.pack_padded_sequence,然后准备被RNN吸收 -
如果我们在GPU上,它会计算所有张量
-
它调用另一个助手函数来为小批量获取合适的0/1掩码
然后,我们通过管道将get_mini_batch()到...里面elbo.step(...)。回想一下,这些参数将被进一步传送到model(...)和guide(...)在中构建梯度估计器的过程中elbo。最后,我们返回一个float,它是对小批量损失的有噪声的估计。
我们现在已经具备了训练循环主要部分所需的所有要素:
times = [time.time()]
for epoch in range(args.num_epochs):
# accumulator for our estimate of the negative log likelihood
# (or rather -elbo) for this epoch
epoch_nll = 0.0
# prepare mini-batch subsampling indices for this epoch
shuffled_indices = np.arange(N_train_data)
np.random.shuffle(shuffled_indices)
# process each mini-batch; this is where we take gradient steps
for which_mini_batch in range(N_mini_batches):
epoch_nll += process_minibatch(epoch, which_mini_batch, shuffled_indices)
# report training diagnostics
times.append(time.time())
epoch_time = times[-1] - times[-2]
log("[training epoch %04d] %.4f \\t\\t\\t\\t(dt = %.3f sec)" %
(epoch, epoch_nll / N_train_time_slices, epoch_time))在每个时期的开始,我们打乱指向训练数据的索引。然后,我们处理每一个小批量,直到我们完成了整个训练集,在我们进行的过程中累积训练损失。最后,我们报告一些诊断信息。注意,我们通过训练集中的时间片总数来归一化损失(这允许我们与参考文献[1]进行比较)。
估价¶
这个训练循环仍然缺少任何类型的评估诊断。让我们解决这个问题。首先,我们需要为评估准备验证和测试数据。由于验证和测试数据集足够小,我们可以很容易地将它们放入内存,我们将分批处理每个数据集(即,我们不会将数据集分成小批)。[旁白:在这一点上,读者可能会问为什么我们不为训练集做同样的事情。原因在于,由于数据二次采样而产生的额外随机性在优化过程中通常是有利的:特别是它可以帮助我们避免局部最优。]事实上,为了获得ELBO更少的噪声估计,我们将计算多样本估计。最简单的方法如下:
val_loss = svi.evaluate_loss(val_batch, ..., num_particles=5)然而,这将涉及一个明确的for循环五次迭代。对于我们的特定模型,我们可以做得更好,并对整个计算进行矢量化。目前在Pyro中实现这一点的唯一方法是显式复制数据n_eval_samples很多次。这是我们遵循的策略:
# package repeated copies of val/test data for faster evaluation
# (i.e. set us up for vectorization)
def rep(x):
return np.repeat(x, n_eval_samples, axis=0)
# get the validation/test data ready for the dmm: pack into sequences, etc.
val_seq_lengths = rep(val_seq_lengths)
test_seq_lengths = rep(test_seq_lengths)
val_batch, val_batch_reversed, val_batch_mask, val_seq_lengths = poly.get_mini_batch(
np.arange(n_eval_samples * val_data_sequences.shape[0]), rep(val_data_sequences),
val_seq_lengths, cuda=args.cuda)
test_batch, test_batch_reversed, test_batch_mask, test_seq_lengths = \
poly.get_mini_batch(np.arange(n_eval_samples * test_data_sequences.shape[0]),
rep(test_data_sequences),
test_seq_lengths, cuda=args.cuda)现在测试和验证数据已经准备好了,我们定义执行评估的辅助函数:
def do_evaluation():
# put the RNN into evaluation mode (i.e. turn off drop-out if applicable)
dmm.rnn.eval()
# compute the validation and test loss
val_nll = svi.evaluate_loss(val_batch, val_batch_reversed, val_batch_mask,
val_seq_lengths) / np.sum(val_seq_lengths)
test_nll = svi.evaluate_loss(test_batch, test_batch_reversed, test_batch_mask,
test_seq_lengths) / np.sum(test_seq_lengths)
# put the RNN back into training mode (i.e. turn on drop-out if applicable)
dmm.rnn.train()
return val_nll, test_nll我们简单地称之为evaluate_loss...的方法elbo,它采用与相同的参数step(),即传递给模型和指南的参数。请注意,我们必须让RNN进入和退出评估模式,以解决辍学问题。我们现在可以坚持do_evaluation()进入训练循环;看见源代码详情请见。
结果¶
让我们确保我们的实现给出合理的结果。我们可以使用参考文献[1]中报告的数字作为健全性检查。对于相同的数据集和相似的模型/向导设置(潜在空间的维度、RNN中隐藏单元的数量等)。)他们报告的归一化负对数似然(NLL)为6.93在测试集上(越低越好§)§。这将与我们的结果相比较6.87。这些数字非常接近,这令人放心。看起来,至少对于这个数据集来说,不使用KL散度的解析表达式不会降低学习模型的质量(尽管如上所述,训练可能需要更长的时间)。
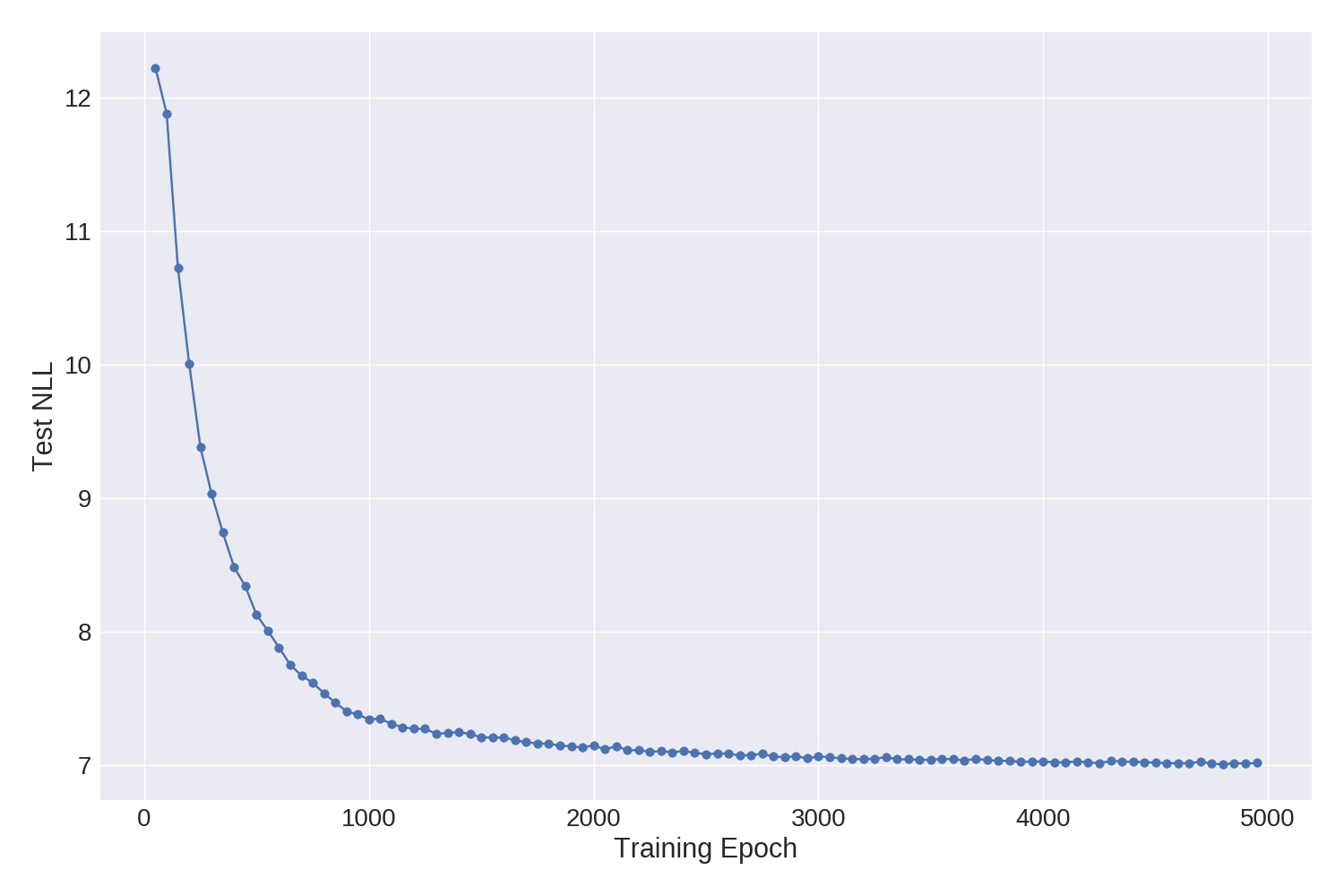
图3:随着样本训练运行的训练进行,测试集NLL上的进度。
在图中,我们显示了测试NLL在单个样本运行(具有相当保守的学习率)的训练期间如何进展。大部分的进步是在前3000个纪元左右,如果我们让训练持续更长时间,会有一些边际收益。在GeForce GTX 1080上,5000个epochs需要大约20个小时。
num_iafs |
测试NLL |
|---|---|
0 |
6.87 |
1 |
6.82 |
2 |
6.80 |
最后,我们还报告了在组合中使用标准化流的指南的结果(细节将在下一节中找到)。
§§实际上,他们似乎报告了同一个型号/指南的两个数字------6.93和7.03,并且不完全清楚这两个报告的数字有什么不同。
铃铛、口哨和其他改进¶
反向自回归流¶
概率编程语言的一大优点是它鼓励模块化。让我们展示一个DMM环境中的例子。我们将通过向混合中添加归一化流来使我们的变分分布更加丰富(参见参考文献[2]中的讨论)。这只会让我们多花四行代码!
首先,在DMM我们添加的构造函数
iafs = [AffineAutoregressive(AutoRegressiveNN(z_dim, [iaf_dim])) for _ in range(num_iafs)]
self.iafs = nn.ModuleList(iafs)这实例化了num_iafs的许多双射变换AffineAutoregressive类型(见参考文献[3,4]);每个规格化流将具有iaf_dim许多隐藏的单位。然后,我们将规范化流程捆绑在一个nn.ModuleList;这只是打包一系列nn.Module南接下来,在指南中,我们添加行
if self.iafs.__len__() > 0:
z_dist = TransformedDistribution(z_dist, self.iafs)这里我们取的是基本分布z_dist,在我们的例子中是一个条件高斯分布,使用TransformedDistribution构造我们将它转换成非高斯分布,即,通过构造,比基本分布更丰富。瞧啊。
检查点¶
如果我们想从训练循环中的灾难性失败中恢复,我们需要跟踪两种状态。首先是模型和向导的各种参数。第二个是优化器的状态(例如,在Adam中,这将包括每个参数的最近梯度估计的运行平均值)。
在Pyro中,所有参数都可以在ParamStore。然而,PyTorch也通过parameters()...的方法nn.Module。因此,我们保存模型和指南参数的一个简单方法是使用state_dict()...的方法dmm共同torch.save();见下文。在这种情况下AffineAutoregressive这是我们唯一的选择。这是因为AffineAutoregressive模块包含PyTorch术语中所谓的"持久缓冲区"。这些东西带有状态,但不是Parameter南这state_dict()和load_state_dict()的方法nn.Module知道如何正确处理缓冲液。
为了保存优化器的状态,我们必须使用pyro.optim.PyroOptim。回想一下,典型的用户从不与PyTorch直接交互Optimizers使用Pyro时;由于参数可以在任意概率程序中动态创建,Pyro需要管理Optimizers为了我们。在我们的例子中,保存优化器状态就像调用optimizer.save()。加载逻辑完全类似。因此,我们保存和加载检查点的整个逻辑只需要几行代码:
# saves the model and optimizer states to disk
def save_checkpoint():
log("saving model to %s..." % args.save_model)
torch.save(dmm.state_dict(), args.save_model)
log("saving optimizer states to %s..." % args.save_opt)
optimizer.save(args.save_opt)
log("done saving model and optimizer checkpoints to disk.")
# loads the model and optimizer states from disk
def load_checkpoint():
assert exists(args.load_opt) and exists(args.load_model), \
"--load-model and/or --load-opt misspecified"
log("loading model from %s..." % args.load_model)
dmm.load_state_dict(torch.load(args.load_model))
log("loading optimizer states from %s..." % args.load_opt)
optimizer.load(args.load_opt)
log("done loading model and optimizer states.")一些最后的评论¶
深度马尔可夫模型是一个相对复杂的模型。既然我们已经努力实现了一个为复调音乐数据集定制的深度马尔可夫模型版本,我们应该问问自己我们还能做什么。如果我们得到一个不同的序列数据集呢?我们必须从头开始吗?
一点也不!概率编程的美妙之处在于它支持------并鼓励------模块化的建模和推理方法。使我们的复调音乐模型适应具有连续观察的数据集就像改变观察可能性一样简单。绝大多数代码可以不加修改地被接管。这意味着,只要做一点额外的工作,本教程中的代码就可以重新用于支持各种不同的模型。
请参阅上的完整代码开源代码库.
参考¶
1\] `Structured Inference Networks for Nonlinear State Space Models`拉胡尔·克里希南、尤里·沙利特、戴维·桑塔格 \[2\] `Variational Inference with Normalizing Flows`、达尼洛·希门尼斯·雷森德、沙基尔·穆罕默德 \[3\] `Improving Variational Inference with Inverse Autoregressive Flow`、迪德里克·金马、蒂姆·萨利曼斯、拉斐尔·约泽福维茨、陈曦、伊利亚·苏茨基弗、马克斯·韦林 \[4\] `MADE: Masked Autoencoder for Distribution Estimation`马修·热尔曼,凯罗尔·格雷戈,伊恩·默里,雨果·拉罗彻尔 \[5\] `Modeling Temporal Dependencies in High-Dimensional Sequences:` `Application to Polyphonic Music Generation and Transcription`、布朗热-莱万多夫斯基、本吉奥和文森特 [以前的](https://pyro.ai/examples/vae_flow_prior.html "以前的") [然后](https://pyro.ai/examples/air.html "然后")