【通俗理解】神经网络Grokking现象的电路效率公式
论文地址:
https://arxiv.org/abs/2309.02390
参考链接:
1\]https://x.com/VikrantVarma_/status/1699823229307699305
\[2\]https://pair.withgoogle.com/explorables/grokking/
### 关键词提炼
#Grokking现象 #神经网络 #电路效率 #学习效率 #一般化解 #记忆化解 #临界数据集大小
### 第一节:Grokking现象的类比与核心概念
#### 1.1 Grokking现象的类比
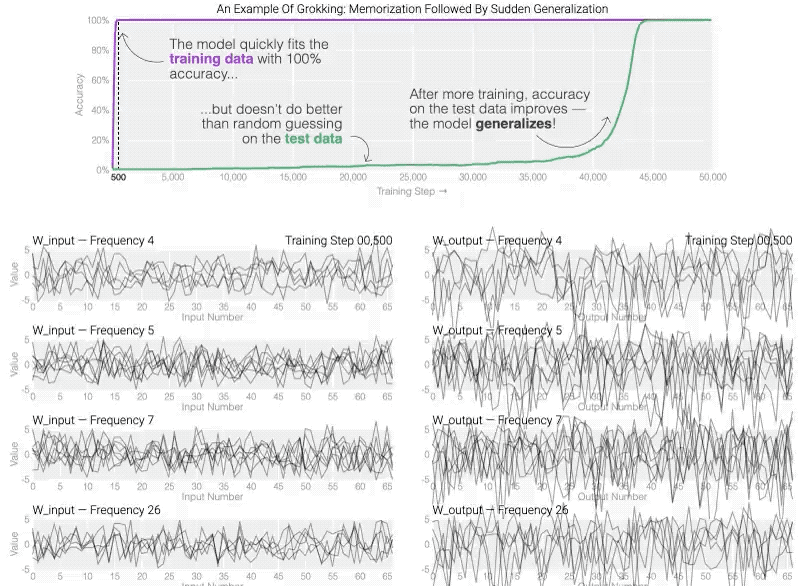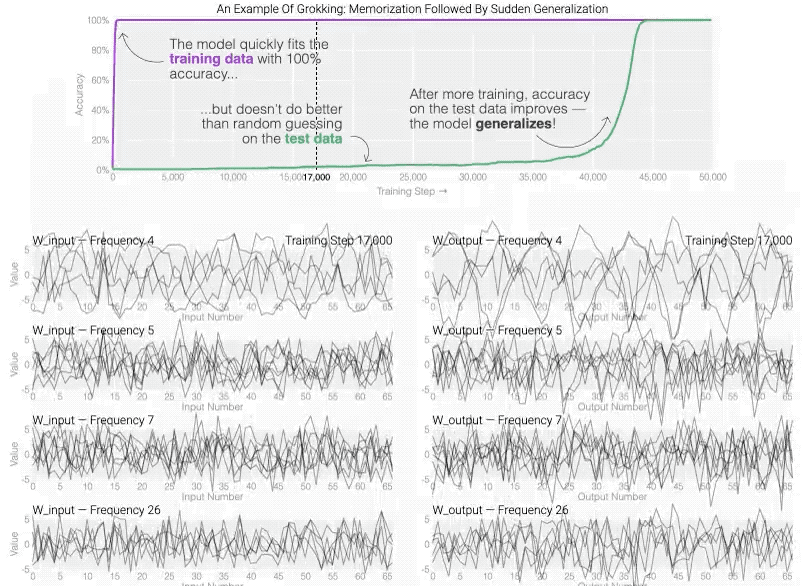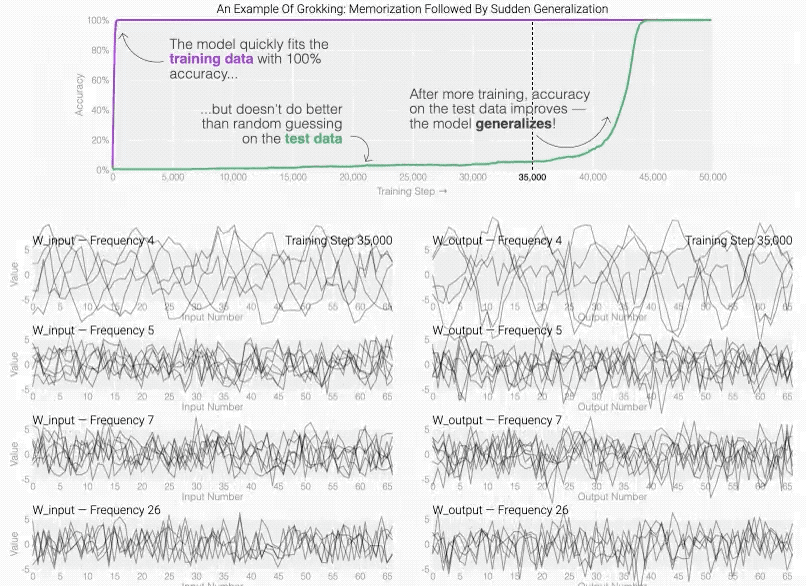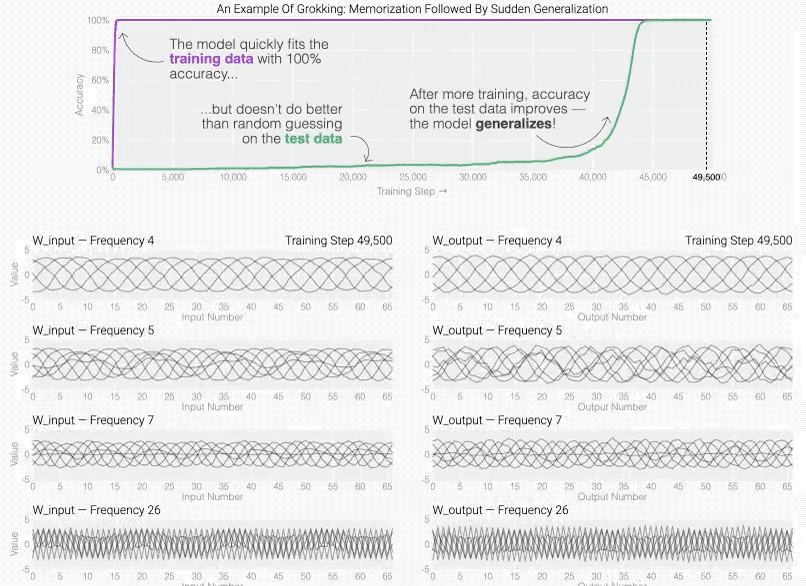
> Grokking现象是神经网络中一个神秘的现象: 在训练初期,网络虽然训练精度完美,但泛化能力极差;
>
> 然而,在持续训练下,它突然实现了完美的泛化。
>
> 这就像一位学生,开始时只能死记硬背答案,但在某个转折点后,他突然能够灵活运用知识,解决了所有问题。
#### 1.2 相似概念比对
* **机器学习中的过拟合与欠拟合**:过拟合指的是模型在训练数据上表现过好,但在新数据上表现不佳;欠拟合则是模型在训练数据和新数据上都表现不佳。Grokking现象可以被视为一种从过拟合到恰当拟合的转变。
* **神经网络学习曲线**:学习曲线描述了训练集和验证集准确率随训练轮次的变化。Grokking现象则是一个特别的学习曲线形态,即在长时间无显著改善后突然跳跃至高水平。

### 第二节:Grokking现象的核心概念与应用
#### 2.1 核心概念
| 核心概念 | 定义 | 比喻或解释 |
|------------------------------|----------------------------------------------|----------------------------------|
| 一般化解 (Generalising Solution) | 能够有效泛化到新数据的神经网络参数配置。 | 类似于掌握了一种解题方法,能应用于各种题型。 |
| 记忆化解 (Memorising Solution) | 仅通过记忆训练数据达到高训练精度的神经网络参数配置。 | 类似于死记硬背答案,换一套题就不会做了。 |
| 电路效率 | 在相同参数规模下,不同参数配置产生的logits(模型输出)的大小,反映学习的难易程度。 | 就像电路中能量转换的效率,高效的电路能在同样输入下产生更多输出。 |
#### 2.2 优势与劣势
| 方面 | 描述 |
|----|-------------------------------------------|
| 优势 | 提供了一种解释神经网络复杂学习行为的框架,帮助研究者更好地理解何时、如何优化模型。 |
| 劣势 | Grokking现象的具体机制和触发条件仍不完全清晰,需要进一步实验验证。 |
### 第三节:公式探索与推演运算
#### 3.1 Grokking现象的假设公式
虽然原文献中没有直接给出具体的数学公式,但我们可以根据其核心思想构建一个简化的模型框架:
GeneralisationEfficiency ( G ) = LogitOutput ( G ) ParameterNorm ( G ) \\text{GeneralisationEfficiency}(G) = \\frac{\\text{LogitOutput}(G)}{\\text{ParameterNorm}(G)} GeneralisationEfficiency(G)=ParameterNorm(G)LogitOutput(G)
MemorisationEfficiency ( M ) = LogitOutput ( M ) ParameterNorm ( M ) \\text{MemorisationEfficiency}(M) = \\frac{\\text{LogitOutput}(M)}{\\text{ParameterNorm}(M)} MemorisationEfficiency(M)=ParameterNorm(M)LogitOutput(M)
其中, GeneralisationEfficiency ( G ) \\text{GeneralisationEfficiency}(G) GeneralisationEfficiency(G) 和 MemorisationEfficiency ( M ) \\text{MemorisationEfficiency}(M) MemorisationEfficiency(M) 分别代表一般化解和记忆化解的电路效率, LogitOutput \\text{LogitOutput} LogitOutput 表示在相同输入下,由不同参数配置产生的logits输出, ParameterNorm \\text{ParameterNorm} ParameterNorm 表示参数向量的范数,作为衡量参数规模的基准。
#### 3.2 公式推演与假设
根据假设,随着训练数据集的增大,记忆化解的效率会下降(因为记忆所有数据变得更为困难),而一般化解的效率则相对保持稳定或缓慢上升。因此,存在一个临界数据集大小 D c r i t i c a l D_{critical} Dcritical,使得:
MemorisationEfficiency ( M D \> D c r i t i c a l ) \< GeneralisationEfficiency ( G D \> D c r i t i c a l ) \\text{MemorisationEfficiency}(M_{D \> D_{critical}}) \< \\text{GeneralisationEfficiency}(G_{D \> D_{critical}}) MemorisationEfficiency(MD\>Dcritical)\