可以说,到现在我们才真正接触到深度网络。最简单的深度网络称为多层感知机。
多层感知机由多层神经元组成,每一层与它的上一层相连,从中接收输入;同时每一层也与它的下一层相连,影响当前层的神经元。
和以前相同,先介绍它的基本内容,再从零开始实现,最后利用 Pytorch 框架简洁实现。
一、多层感知机
隐藏层
回想一下我们上一节中的 softmax 模型架构,该模型通过线性变换将输入映射为输出,然后进行 softmax 操作。
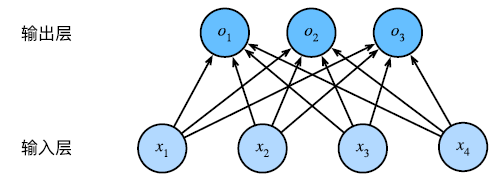
但是,这样的线性模型可能会出错。线性意味着单调,即如果权重为正的话,任何特征的增大都将引起输出的增大。
有时这样的模型是适合的,且我们还可以通过一些处理(如对数运算),使得线性模型能够起作用。
然而,现实生活中更多的是不单调的情况。例如,根据体温预测死亡率,对于高于 37 度的人来说,体温越高越危险;而对于低于 37 度的人来说,温度越高,风险越低。
再想想我们上一节实现的分类问题,一张 28 × 28 28\times28 28×28 的图片,我们将其视为了具有 784 个特征的输入,分别对应于 784 个像素点。
我们增强某个像素的强度,是否就能增大这张图片属于某个类别的概率呢?显然是不会的。
图像分类的结果与图片的像素强度具有更加复杂的关系,并且我们也难以通过一些简单的变换使得线性模型可行。
我们可以在网络中加入一个或多个隐藏层来克服线性模型的缺陷,使其能处理更复杂的函数关系。
其中一个简单的办法是将许多全连接层堆叠在一起。每一层输出的上面的层,直到生成最后的输出。这种架构通常称为多层感知机(multilayer perceptron, MLP)。
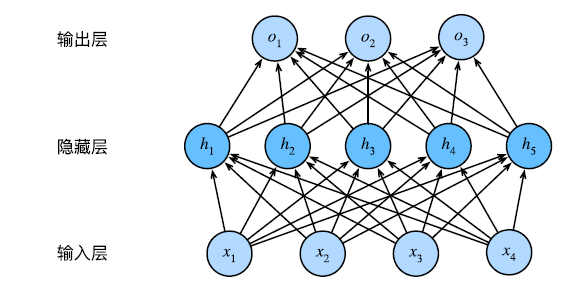
这个多层感知机有 4 个输入,3 个输出,其隐藏层包含 5 个 隐藏单元。
输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐层和输出层的计算,故该多层感知机的层数为 2。
但是,加入了一层隐藏层后,实际上输入和输出还是线性关系,因为线性关系嵌套还是线性的。
为了发挥多层架构的潜力,我们还需要一个额外的因素:在线性变换之后对每个隐藏单元应用非线性的激活函数(activation function)。激活函数的输出被称为活性值(activations)。
一般来说,有了激活函数,就不可能再将我们的多层感知机退化为线性模型。
激活函数
激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活,它们将输入信号转换为输出的可微运算。常见的激活函数有:
1. ReLU 函数
因为修正线性单元(Rectified linear unit, ReLU)实现简单,同时在各种预测任务中表现良好,因此它广受欢迎。
ReLU 提供了一种非常简单的非线性变换。给定元素 x x x,ReLU 函数被定义为该元素与 0 的最大值。
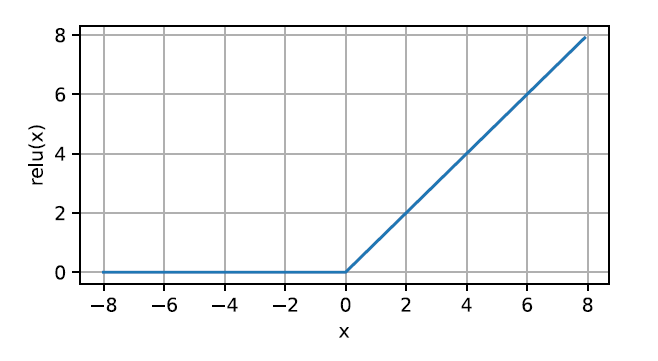
2. Sigmoid 函数
对于一个定义域在 R R R 中的输入,sigmoid 函数将输入变换为区间(0, 1)上的输出。因此,sigmoid 通常被称为挤压函数。
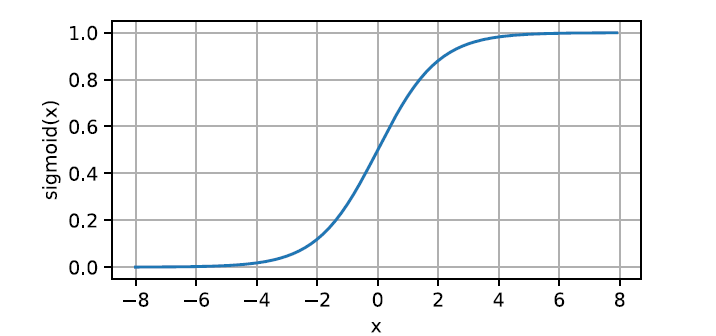
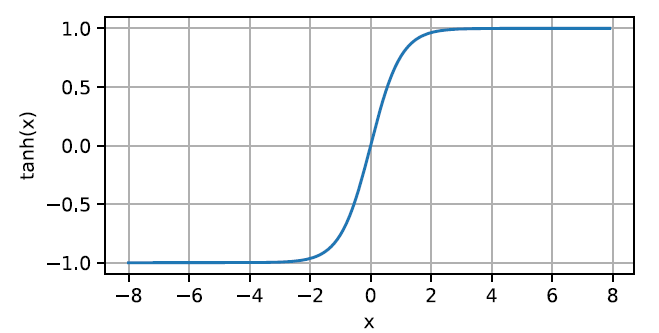
3. tanh 函数
与 sigmoid 函数类似,tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。
二、多层感知机的从零开始实现
我们继续研究上一节的分类问题,同样使用 Fashion-MNIST 数据集。
初始化模型参数
回想一下我们在 softmax 里的初始化,因为 softmax 回归只有一层,故只需要初始化一个权重向量和一个偏置即可。
多层感知机多了一层线性层,故共有 4 个模型参数,隐藏层的权重、偏置以及输出层的权重及偏置。
此外,隐藏层的宽度需要我们确定,其可视为一个超参数。一般我们取 2 的若干次幂,且介于输入大小和输出大小之间,这里我们选择 256。
隐层的参数形状为 784 × 256 784\times 256 784×256,而输出层参数的形状为 256 × 10 256\times10 256×10。
python
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]定义激活函数
这里我们选择 ReLU,用于处理隐层的输出,再出入输出层。
python
def relu(X): # 激活函数
a = torch.zeros_like(X)
return torch.max(X, a)定义模型
有了激活函数后,模型的定义可直接使用矩阵乘法实现。
python
def net(X): # 模型
X = X.reshape((-1, num_inputs)) # 展平
H = relu(X@W1 + b1) # 这里"@"代表矩阵乘法
return (H@W2 + b2)定义损失函数
这里我们通用采用交叉熵损失。值得一提的是,直接调用的 nn 模块里的交叉熵损失函数,它里面就包含了 softmax 操作。
python
loss = nn.CrossEntropyLoss(reduction='none') # 损失函数训练
多层感知机的训练和 softmax 大差不差,直接用我们之前写好的那个训练函数。
python
num_epochs, lr = 10, 0.1
optimizer = torch.optim.SGD(params, lr=lr)
train(net, train_iter, test_iter, loss, num_epochs, optimizer)得到的结果为如下。可以发现,加了激活函数后,训练损失倒小了不少,但测试集精度并未有明显提升。
第10轮的训练损失为0.3840572128295898
第10轮的训练精度为0.8638666666666667
第10轮的测试集精度为0.8394有了前面线性回归和 softmax 回归的基础,这里实现起来是很轻松的,只是模型参数多了需要单独初始化有些麻烦。
下面我们看看简洁实现。
三、多层感知机的简洁实现
定义模型与初始化参数
调用框架的话,在定义模型调用 nn.Sequential 时,注意有 4 层,第一层展平,第二层隐层,第三层激活,第四层输出。
模型的初始化可以利用前面定义过的初始化权重函数init_weights()。
python
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10)) # 定义模型
net = net.to(try_gpu())
net.apply(init_weights) # 初始化模型参数训练
可以直接把 softmax 回归的简洁实现代码复制过来,把定义模型和初始化参数的部分改了,就 OK 了。
训练情况如下:
python
第10轮的训练损失为0.3854055678049723
第10轮的训练精度为0.86335
第10轮的测试集精度为0.8503两种实现方式的代码见资源。