LeetCode //C - 363. Max Sum of Rectangle No Larger Than K

363. Max Sum of Rectangle No Larger Than K

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.

Example 1:

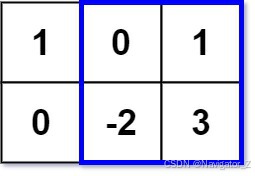
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:

Input: matrix = [[2,2,-1]], k = 3
Output: 3

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
− 1 0 5 < = k < = 1 0 5 -10^5 <= k <= 10^5 −105<=k<=105

From: LeetCode

Link: 363. Max Sum of Rectangle No Larger Than K

Solution:

Ideas:

Outer loops: We loop over all pairs of starting and ending rows.
Column sum array: We calculate the cumulative sums for columns between the two rows, effectively reducing the 2D matrix to a 1D array problem.
Brute-force subarray sum check: We calculate all possible sums of subarrays in the 1D colSums array and track the largest one that is no larger than k.

Code:

c 复制代码

int maxSumSubmatrix(int** matrix, int matrixSize, int* matrixColSize, int k) {
    int maxSum = INT_MIN;
    int rows = matrixSize, cols = *matrixColSize;

    // Loop through the possible row start points
    for (int startRow = 0; startRow < rows; ++startRow) {
        // Temporary array to store column sums
        int* colSums = (int*)calloc(cols, sizeof(int));
        
        // Loop through the possible row end points
        for (int endRow = startRow; endRow < rows; ++endRow) {
            // Update column sums
            for (int col = 0; col < cols; ++col) {
                colSums[col] += matrix[endRow][col];
            }

            // Now we need to find the subarray no larger than k in the colSums array
            // Brute-force approach for subarray sums
            for (int startCol = 0; startCol < cols; ++startCol) {
                int currentSum = 0;
                for (int endCol = startCol; endCol < cols; ++endCol) {
                    currentSum += colSums[endCol];
                    if (currentSum <= k) {
                        if (currentSum > maxSum) {
                            maxSum = currentSum;
                        }
                    }
                }
            }
        }
        free(colSums);
    }

    return maxSum;
}