本章介绍图像分类和图像内容分类算法。首先,我们介绍一些简单而有效的方法和目前一些性能最好的分类器,并运用它们解决两类和多类分类问题,最后展示两个用于手势识别和目标识别的应用实例。
8.1 K邻近分类法(KNN)
在分类方法中,最简单且用得最多的一种方法之一就是 KNN(K-Nearest Neighbor ,K邻近分类法),这种算法把要分类的对象(例如一个特征向量)与训练集中已知类标记的所有对象进行对比,并由 k 近邻对指派到哪个类进行投票。这种方法通常分类效果较好,但是也有很多弊端:与 K-means 聚类算法一样,需要预先设定 k 值,k 值的选择会影响分类的性能;此外,这种方法要求将整个训练集存储起来,如果训练集非常大,搜索起来就非常慢。对于大训练集,采取某些装箱形式通常会减少对比的次数 1 从积极的一面来看,这种方法在采用何种距离度量方面是没有限制的;实际上,对于你所能想到的东西它都可以奏效,但这并不意味着对任何东西它的分类性能都很好。另外,这种算法的可并行性也很一般。实现最基本的 KNN 形式非常简单。给定训练样本集和对应的标记列表,下面的代码可以用来完成这一工作。这些训练样本和标记可以在一个数组里成行摆放或者干脆摆放列表里,训练样本可能是数字、字符串等任何你喜欢的形状。将定义的类对象添加到名为 knn.py 的文件里:
class KnnClassifier(object):
def init(self,labels,samples):
""" 使用训练数据初始化分类器 """
self.labels = labels
self.samples = samples
def classify(self,point,k=3):
""" 在训练数据上采用 k 近邻分类,并返回标记 """
计算所有训练数据点的距离
dist = array([L2dist(point,s) for s in self.samples])
对它们进行排序
ndx = dist.argsort()
用字典存储 k 近邻
votes = {}
for i in range(k):
label = self.labels[ndx[i]]
votes.setdefault(label,0)
votes[label] += 1
return max(votes)
def L2dist(p1,p2):
return sqrt( sum( (p1-p2)**2) )
定义一个类并用训练数据初始化非常简单 ; 每次想对某些东西进行分类时,用 KNN方法,我们就没有必要存储并将训练数据作为参数来传递。用一个字典来存储邻近标记,我们便可以用文本字符串或数字来表示标记。在这个例子中,我们用欧式距离 (L2) 进行度量,当然,如果你有其他的度量方式,只需要将其作为函数添加到上面代码的最后。
8.1.1 一个简单的二维示例
我们首先建立一些简单的二维示例数据集来说明并可视化分类器的工作原理,下面的脚本将创建两个不同的二维点集,每个点集有两类,用 Pickle 模块来保存创建的数据:
from numpy.random import randn
import pickle
创建二维样本数据
n = 200
两个正态分布数据集
class_1 = 0.6 * randn(n,2)
class_2 = 1.2 * randn(n,2) + array([5,1])
labels = hstack((ones(n),-ones(n)))
用 Pickle 模块保存
with open('points_normal.pkl', 'w') as f:
pickle.dump(class_1,f)
pickle.dump(class_2,f)
pickle.dump(labels,f)
正态分布,并使数据成环绕状分布
class_1 = 0.6 * randn(n,2)
r = 0.8 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))
用 Pickle 保存
with open('points_ring.pkl', 'w') as f:
pickle.dump(class_1,f)
pickle.dump(class_2,f)
pickle.dump(labels,f)
用不同的保存文件名运行该脚本两次,例如第一次用代码中的文件名进行保存,第二次将代码中的 points_normal_t.pkl 和 points_ring_pkl 分别改为 points_normal_test.pkl 和 points_ring_test.pkl 进行保存。你将得到 4 个二维数据集文件,每个分布都有两个文件,我们可以将一个用来训练,另一个用来做测试。让我们看看怎么用 KNN 分类器来完成,用下面的代码来创建一个脚本:
import pickle
import knn
import imtools
用 Pickle 载入二维数据点
with open('points_normal.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
这里用 Pickle 模块来创建一个 kNN 分类器模型。现在在上面代码后添加下面的代码:
用 Pickle 模块载入测试数据
with open('points_normal_test.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
在测试数据集的第一个数据点上进行测试
print model.classify(class_1[0])
上面代码载入另一个数据集(测试数据集),并在你的控制台上打印第一个数据点估计出来的类标记。
为了可视化所有测试数据点的分类,并展示分类器将两个不同的类分开得怎样,我们可以添加这些代码:
定义绘图函数
def classify(x,y,model=model):
return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])
绘制分类边界
imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
show()
这里我们创建了一个简短的辅助函数以获取 x 和 y 二维坐标数组和分类器,并返回一个预测的类标记数组。现在我们把函数作为参数传递给实际的绘图函数。把下面的函数添加到文件 imtools 中:
def plot_2D_boundary(plot_range,points,decisionfcn,labels,values=[0]):
"""Plot_range 为(xmin,xmax,ymin,ymax),points 是类数据点列表,
decisionfcn 是评估函数,labels 是函数 decidionfcn 关于每个类返回的标记列表 """
clist = ['b','r','g','k','m','y'] # 不同的类用不同的颜色标识
在一个网格上进行评估,并画出决策函数的边界
x = arange(plot_range[0],plot_range[1],.1)
y = arange(plot_range[2],plot_range[3],.1)
xx,yy = meshgrid(x,y)
xxx,yyy = xx.flatten(),yy.flatten() # 网格中的 x,y 坐标点列表
zz = array(decisionfcn(xxx,yyy))
zz = zz.reshape(xx.shape)
以 values 画出边界
contour(xx,yy,zz,values)
对于每类,用 * 画出分类正确的点,用 o 画出分类不正确的点
for i in range(len(points)):
d = decisionfcn(points[i][:,0],points[i][:,1])
correct_ndx = labels[i]==d
incorrect_ndx = labels[i]!=d
plot(points[i][correct_ndx,0],points[i][correct_ndx,1],'*',color=clist[i])
plot(points[i][incorrect_ndx,0],points[i][incorrect_ndx,1],'o',color=clist[i])
axis('equal')
这个函数需要一个决策函数(分类器),并且用 meshgrid() 函数在一个网格上进行预测。决策函数的等值线可以显示边界的位置,默认边界为零等值线。画出来的结果如图 8-1 所示,正如你所看到的,kNN 决策边界适用于没有任何明确模型的类分布。
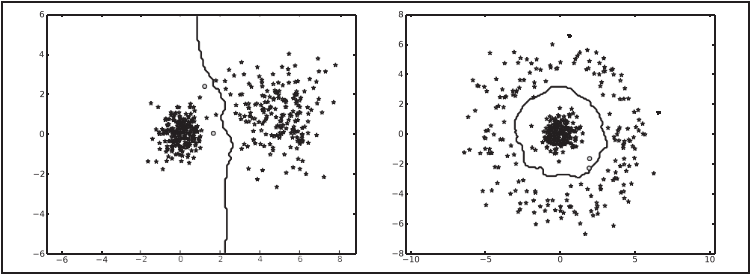
图 8-1:用 K 邻近分类器分类二维数据。每个示例中,不同颜色代表类标记,正确分类的点用星号表示,分类错误的点用圆点表示,曲线是分类器的决策边界
8.1.2 用稠密SIFT作为图像特征
我们来看如何对图像进行分类。要对图像进行分类,我们需要一个特征向量来表示一幅图像。在聚类一章我们用平均 RGB 像素值和 PCA 系数作为图像的特征向量;这里我们会介绍另外一种表示形式,即稠密 SIFT 特征向量。
在整幅图像上用一个规则的网格应用 SIFT 描述子可以得到稠密 SIFT 的表示形式 1 ,我们可以利用 2.2 节的可执行脚本,通过添加一些额外的参数来得到稠密 SIFT 特征。创建一个名为 dsift.py 的文件,并添加下面代码到该文件中:
import sift
def process_image_dsift(imagename,resultname,size=20,steps=10,
force_orientation=False,resize=None):
""" 用密集采样的 SIFT 描述子处理一幅图像,并将结果保存在一个文件中。可选的输入:
特征的大小 size,位置之间的步长 steps,是否强迫计算描述子的方位 force_orientation
(False 表示所有的方位都是朝上的),用于调整图像大小的元组 """
im = Image.open(imagename).convert('L')
if resize!=None:
im = im.resize(resize)
m,n = im.size
if imagename[-3:] != 'pgm':
创建一个 pgm 文件
im.save('tmp.pgm')
imagename = 'tmp.pgm'
创建帧,并保存到临时文件
scale = size/3.0
x,y = meshgrid(range(steps,m,steps),range(steps,n,steps))
xx,yy = x.flatten(),y.flatten()
frame = array([xx,yy,scale*ones(xx.shape[0]),zeros(xx.shape[0])])
savetxt('tmp.frame',frame.T,fmt='%03.3f')
if force_orientation:
cmmd = str("sift "+imagename+" --output="+resultname+
" --read-frames=tmp.frame --orientations")
else:
cmmd = str("sift "+imagename+" --output="+resultname+
" --read-frames=tmp.frame")
os.system(cmmd)
print 'processed', imagename, 'to', resultname
对比 2.2 节的 process_image() 函数,为了使用命令行处理,我们用 savetxt() 函数将帧数组存储在一个文本文件中,该函数的最后一个参数可以在提取描述子之前对图像的大小进行调整,例如,传递参数 imsize=(100, 100) 会将图像调整为 100×100像素的方形图像。最后,如果 force_orientation 为真,则提取出来的描述子会基于
局部主梯度方向进行归一化;否则,则所有的描述子的方向只是简单地朝上。
利用类似下面的代码可以计算稠密 SIFT 描述子,并可视化它们的位置:
import dsift,sift
dsift.process_image_dsift('empire.jpg','empire.sift',90,40,True)
l,d = sift.read_features_from_file('empire.sift')
im = array(Image.open('empire.jpg'))
sift.plot_features(im,l,True)
show()
使用用于定位描述子的局部梯度方向(force_orientation 设置为真),该代码可以在整个图像中计算出稠密 SIFT 特征。图 8-2 显示出了这些位置。

图 8-2:在一幅图像上应用稠密 SIFT 描述子的例子
8.1.3 图像分类:手势识别
在这个应用中,我们会用稠密 SIFT 描述子来表示这些手势图像,并建立一个简单的手势识别系统。我们用静态手势(Static Hand Posture)数据库(参见 http://www.idiap.ch/resource/gestures/)中的一些图像进行演示。在该数据库主页上下载数据较小的测试集 test set 16.3Mb,将下载后的所有图像放在一个名为 uniform 的文件夹里,每一类均分两组,并分别放入名为 train 和 test 的两个文件夹中。用上面的稠密 SIFT 函数对图像进行处理,可以得到所有图像的特征向量。这里,再次假设列表 imlist 中包含了所有图像的文件名,可以通过下面的代码得到每幅图像的稠密 SIFT 特征:
import dsift
将图像尺寸调为 (50,50),然后进行处理
for filename in imlist:
featfile = filename[:-3]+'dsift'
dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))
上面代码会对每一幅图像创建一个特征文件,文件名后缀为 .dsift。注意,这里将图像分辨率调成了常见的固定大小。这是非常重要的,否则这些图像会有不同数量的描述子,从而每幅图像的特征向量长度也不一样,这将导致在后面比较它们时出错。图 8-3 绘制出了一些带有描述子的图像。

图 8-3:6 类简单手势图像的稠密 SIFT 描述子,图像来源于静态手势(Static Hand Posture)数据库
定义一个辅助函数,用于从文件中读取稠密 SIFT 描述子,如下:
import os, sift
def read_gesture_features_labels(path):
对所有以 .dsift 为后缀的文件创建一个列表
featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
读取特征
features = []
for featfile in featlist:
l,d = sift.read_features_from_file(featfile)
features.append(d.flatten())
features = array(features)
创建标记
labels = [featfile.split('/')[-1][0] for featfile in featlist]
return features,array(labels)
然后,我们可以用下面的脚本读取训练集、测试集的特征和标记信息:
features,labels = read_gesture_features_labels('train/')
test_features,test_labels = read_gesture_features_labels('test/')
classnames = unique(labels)
这里,我们用文件名的第一个字母作为类标记,用 NumPy 的 unique() 函数可以得到一个排序后唯一的类名称列表。
现在我们可以在该数据上使用前面的 K 近邻代码:
测试 KNN
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
准确率
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print 'Accuracy:', acc
首先,用训练数据及其标记作为输入,创建分类器对象;然后,我们在整个测试集上遍历并用 classify() 方法对每幅图像进行分类。将布尔数组和 1 相乘并求和,可以计算出分类的正确率。由于该例中真值为 1,所以很容易计算出正确分类数。它应该会打印出一个类似下面的结果:
Accuracy: 0.811518324607
这说明该例中有 81% 的图像是正确的。该结果会随 k值及稠密 SIFT 图像描述子参数的选择而变化。虽然上面的正确率显示了对于一给定的测试集有多少图像是正确分类的,但是它并没有告诉我们哪些手势难以分类,或会犯哪些典型错误。混淆矩阵是一个可以显示每类有多少个样本被分在每一类中的矩阵,它可以显示错误的分布情况,以及哪些类是经常相互"混淆"的。
下面的函数会打印出标记及相应的混淆矩阵:
def print_confusion(res,labels,classnames):
n = len(classnames)
混淆矩阵
class_ind = dict([(classnames[i],i) for i in range(n)])
confuse = zeros((n,n))
for i in range(len(test_labels)):
confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
print 'Confusion matrix for'
print classnames
print confuse
运行:
print_confusion(res,test_labels,classnames)
打印输出应该如下:
Confusion matrix for
'A' 'B' 'C' 'F' 'P' 'V'
\[ 26. 0. 2. 0. 1. 1.
0. 26. 0. 1. 1. 1.
0. 0. 25. 0. 0. 1.
0. 3. 0. 37. 0. 0.
0. 1. 2. 0. 17. 1.
3. 1. 3. 0. 14. 24.\]
上面混淆矩阵显示,本例子中 P(Point)经常被误分为"V"。
8.2 贝叶斯分类器
另一个简单却有效的分类器是贝叶斯分类器 1 (或称朴素贝叶斯分类器)。贝叶斯分类器是一种基于贝叶斯条件概率定理的概率分类器,它假设特征是彼此独立不相关的(这就是它"朴素"的部分)。贝叶斯分类器可以非常有效地被训练出来,原因在于每一个特征模型都是独立选取的。尽管它们的假设非常简单,但是贝叶斯分类器已经在实际应用中获得显著成效,尤其是对垃圾邮件的过滤。贝叶斯分类器的另一个好处是,一旦学习了这个模型,就没有必要存储训练数据了,只需存储模型的参数。该分类器是通过将各个特征的条件概率相乘得到一个类的总概率,然后选取概率最高的那个类构造出来的。
首先让我们看一个使用高斯概率分布模型的贝叶斯分类器基本实现,也就是用从训练数据集计算得到的特征均值和方差来对每个特征单独建模。把下面的 Bayes Classifier 类添加到文件 bayes.py 中:
class BayesClassifier(object):
def init(self):
""" 使用训练数据初始化分类器 """
self.labels = [] # 类标签
self.mean = [] # 类均值
self.var = [] # 类方差
self.n = 0 # 类别数
def train(self,data,labels=None):
""" 在数据 data(n ×dim 的数组列表)上训练,标记 labels 是可选的,默认为 0...n-1 """
if labels==None:
labels = range(len(data))
self.labels = labels
self.n = len(labels)
for c in data:
self.mean.append(mean(c,axis=0))
self.var.append(var(c,axis=0))
def classify(self,points):
""" 通过计算得出的每一类的概率对数据点进行分类,并返回最可能的标记 """
计算每一类的概率
est_prob = array([gauss(m,v,points) for m,v in zip(self.mean,self.var)])
获取具有最高概率的索引,该索引会给出类标签
ndx = est_prob.argmax(axis=0)
est_labels = array([self.labels[n] for n in ndx])
return est_labels, est_prob
该模型每一类都有两个变量,即类均值和协方差。train() 方法获取特征数组列表(每个类对应一个特征数组),并计算每个特征数组的均值和协方差。classify() 方法计算数据点构成的数组的类概率,并选概率最高的那个类,最终返回预测的类标记及概率值,同时需要一个高斯辅助函数:
def gauss(m,v,x):
""" 用独立均值 m 和方差 v 评估 d 维高斯分布 """
if len(x.shape)==1:
n,d = 1,x.shape[0]
else:
n,d = x.shape
协方差矩阵,减去均值
S = diag(1/v)
x = x-m
概率的乘积
y = exp(-0.5*diag(dot(x,dot(S,x.T))))
归一化并返回
return y * (2*pi)**(-d/2.0) / ( sqrt(prod(v)) + 1e-6)
该函数用来计算单个高斯分布的乘积,返回给定一组模型参数 m 和 v的概率,更多多元正态分布例子可以参见 http://en.wikipedia.org/wiki/Multivariate_normal_distribution。
将该贝叶斯分类器用于上一节的二维数据,下面的脚本将载入上一节中的二维数据,并训练出一个分类器:
import pickle
import bayes
import imtools
用 Pickle 模块载入二维样本点
with open('points_normal.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
训练贝叶斯分类器
bc = bayes.BayesClassifier()
bc.train([class_1,class_2],[1,-1])
下面我们可以载入上一节中的二维测试数据对分类器进行测试:
用 Pickle 模块载入测试数据
with open('points_normal_test.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
在某些数据点上进行测试
print bc.classify(class_1[:10])[0]
绘制这些二维数据点及决策边界
def classify(x,y,bc=bc):
points = vstack((x,y))
return bc.classify(points.T)[0]
imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
show()
该脚本会将前 10 个二维数据点的分类结果打印输出到控制台,输出结果如下:
1 1 1 1 1 1 1 1 1 1
我们再次用一个辅助函数 classify() 在一个网格上评估该函数来可视化这一分类结果。两个数据集的分类结果如图 8-4 所示;该例中,决策边界是一个椭圆,类似于二维高斯函数的等值线。
图 8-4:用贝叶斯分类器对二维数据进行分类。每个例子中的颜色代表了类标记。正确分类的点用星号表示,误错分类的点用圆点表示,曲线是分类器的决策边界
用PCA降维
现在,我们尝试手势识别问题。由于稠密 SIFT 描述子的特征向量十分庞大(从前面的例子可以看到,参数的选取超过了 10 000),在用数据拟合模型之前进行降维处理是一个很好的想法。主成分分析,即 PCA(见 1.3 节),非常适合用于降维。下面的脚本就是用 pca.py 中的 PCA 进行降维:
import pca
V,S,m = pca.pca(features)
保持最重要的成分
V = V[:50]
features = array([dot(V,f-m) for f in features])
test_features = array([dot(V,f-m) for f in test_features])
这里的 features 和 test_features 与 K 邻近中的例子中加载的数组是一样的。在本例中,我们在训练数据上用 PCA 降维,并保持在这 50 维具有最大的方差。这可以通过均值 m(是在训练数据上计算得到的)并与基向量 V 相乘做到。对测试数据进行同样的转换。
训练并测试贝叶斯分类器如下:
测试贝叶斯分类器
bc = bayes.BayesClassifier()
blist = [features[where(labels==c)[0]] for c in classnames]
bc.train(blist,classnames)
res = bc.classify(test_features)[0]
由于 BayesClassifier 需要获取数组列表(每一类对应一个数组),在把数据传递给train() 函数之前,我们需要对数据进行转换。因为我们目前还不需要概率,所以只需返回预测的类标记。
检查分类准确率:
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print 'Accuracy:', acc
输出如下结果:
Accuracy: 0.717277486911
检查混淆矩阵:
print_confusion(res,test_labels,classnames)
输出如下结果:
Confusion matrix for
'A' 'B' 'C' 'F' 'P' 'V'
\[ 20. 0. 0. 4. 0. 0.
0. 26. 1. 7. 2. 2.
1. 0. 27. 5. 1. 0.
0. 2. 0. 17. 0. 0.
0. 1. 0. 4. 22. 1.
8. 2. 4. 1. 8. 25.\]
虽然分类效果不如 K 邻近分类器,但是贝叶斯分类器不需要保存任何训练数据,而且只需保存每个类的模型参数。这一结果会随着 PCA 维度选取的不同而发生巨大的变化。
8.3 支持向量机
SVM(Support Vector Machine,支持向量机)是一类强大的分类器,可以在很多分类问题中给出现有水准很高的分类结果。最简单的 SVM 通过在高维空间中寻找一个最优线性分类面,尽可能地将两类数据分开。对于一特征向量 x 的决策函数为:
f (x )=w · x -b

这里的 i是从训练集中选出的部分样本,这里选择的样本称为支持向量,因为它们可以帮助定义分类的边界。
SVM 的一个优势是可以使用核函数(kernel function);核函数能够将特征向量映射到另外一个不同维度的空间中,比如高维度空间。通过核函数映射,依然可以保持对决策函数的控制,从而可以有效地解决非线性或者很难的分类问题。用核函数 K (x i , x )替代上面决策函数中的内积 x i · x。

对于多分类问题,通常训练多个 SVM,使每一个 SVM 可以将其中一类与其余类分开,这样的分类器也称为"one-versus-all"分类器。关于 SVM 的更多细节可以参阅 在线文档 http://www.support-vector.net/references.html 。
8.3.1 使用LibSVM
LibSVM[7] 是最好的、使用最广泛的 SVM 实现工具包。LibSVM 为 Python 提供了一个良好的接口(也为其他编程语言提供了接口)。
我们看看 LibSVM 在二维样本数据点上是怎样工作的。下面的脚本会载入在前面kNN 范例分类中用到的数据点,并用径向基函数训练一个 SVM 分类器:
import pickle
from svmutil import *
import imtools
用 Pickle 载入二维样本点
with open('points_normal.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
转换成列表,便于使用 libSVM
class_1 = map(list,class_1)
class_2 = map(list,class_2)
labels = list(labels)
samples = class_1+class_2 # 连接两个列表
创建 SVM
prob = svm_problem(labels,samples)
param = svm_parameter('-t 2')
在数据上训练 SVM
m = svm_train(prob,param)
在训练数据上分类效果如何?
res = svm_predict(labels,samples,m)
我们用与前面一样的方法载入数据集,但是这次需要把数组转成列表,因为LibSVM 不支持数组对象作为输入。这里,我们用 Python 的内建函数 map() 进行转换,map() 函数中用到了对角一个元素都会进行转换的 list() 函数。紧接着我们创建了一个 svm_problem 对象,并为其设置了一些参数。调用 svm_train() 求解该优化问题用以确定模型参数,然后就可以用该模型进行预测了。最后一行调用 svm_predict(),用求得的模型 m对训练数据分类,并显示出在训练数据中分类的正确率,打印输出结果如下:
Accuracy = 100% (400/400) (classification)
结果表明该分类器完全分开了训练数据,400 个数据点全部分类正确。
注意,我们在调用方法训练分类器时添加了一个参数选择字符串,这些参数用于控制核函数的类型、等级及其他选项。尽管其中大部分超出了本书范围,但是需要知道两个重要的参数 t 和 k 。参数 t决定了所用核函数的类型,该选项是:

参数 k决定了多项式的次数(默认为 3)。
现在,载入其他数据集,并对该分类器进行测试:
用 Pickle 模块载入测试数据
with open('points_normal_test.pkl', 'r') as f:
class_1 = pickle.load(f)
class_2 = pickle.load(f)
labels = pickle.load(f)
转换成列表,便于使用 LibSVM
class_1 = map(list,class_1)
class_2 = map(list,class_2)
定义绘图函数
def predict(x,y,model=m):
return array(svm_predict([0]*len(x),zip(x,y),model)[0])
绘制分类边界
imtools.plot_2D_boundary([-6,6,-6,6],[array(class_1),array(class_2)],predict,[-1,1])
show()
我们需要再次为 LibSVM 将数据转成列表,同时和之前一样,我们定义了一个辅助函数 predict() 来绘制分类的边界。注意,如果无法获取真实的标记,我们用([0]*len(x)) 列表来代替标记列表。只要代替的标记列表长度正确,你可以使用任意的列表。图 8-5 显示了两个不同数据集在二维平面上的分布情况。
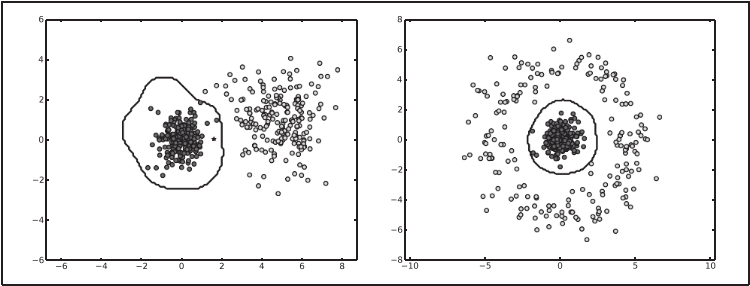
8-5:用支持向量机 SVM 对二维数据进行分类。在这两幅图中,我们用不同颜色标识类标记。正确分类的点用星号表示,错误分类的点用圆点表示,曲线是分类器的决策边界
8.3.2 再论手势识别
在多类手势识别问题上使用 LibSVM 相当直观。LibSVM 可以自动处理多个类,我们只需要对数据进行格式化,使输入和输出匹配 LibSVM 的要求。和之前的例子一样,feature 和 test_features 两个文件中分别数组的形式保存训练数据和测试数据。下面的代码会载入训练数据测试数据,并训练一个线性 SVM 分类器:
features = map(list,features)
test_features = map(list,test_features)
为标记创建转换函数
transl = {}
for i,c in enumerate(classnames):
transl[c],transl[i] = i,c
创建 SVM
prob = svm_problem(convert_labels(labels,transl),features)
param = svm_parameter('-t 0')
在数据上训练 SVM
m = svm_train(prob,param)
在训练数据上分类效果如何
res = svm_predict(convert_labels(labels,transl),features,m)
测试 SVM
res = svm_predict(convert_labels(test_labels,transl),test_features,m)[0]
res = convert_labels(res,transl)
与之前一样,我们调用 map() 函数将数组转成列表;因为 LibSVM 不能处理字符串标记,所以这些标记也需要转换。字典 transl 会包含一个在字符串和整数标记间的变换。你可以试着在控制台上打印该变换,看看其对应变换关系。参数 -t 0 设置分类器是线性分类器,决策边界在 10 000 维特征原空间中是一个超平面。
现在,对标记进行比较:
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print 'Accuracy:', acc
print_confusion(res,test_labels,classnames)
用线性核函数得出的分类结果如下:
Accuracy: 0.916230366492
Confusion matrix for
'A' 'B' 'C' 'F' 'P' 'V'
\[ 26. 0. 1. 0. 2. 0.
0. 28. 0. 0. 1. 0.
0. 0. 29. 0. 0. 0.
0. 2. 0. 38. 0. 0.
0. 1. 0. 0. 27. 1.
3. 0. 2. 0. 3. 27.\]
现在,正如我们在 8.2 节所做的,用 PCA 将维数降低到 50,分类正确率变为:
Accuracy: 0.890052356021
可以看出,当特征向量维数降低到原空间数据维数的 1/200 时,结果并不差(存储支持向量所需占用的空间也减小到原来的 1/200)。
8.4 光学字符识别
作为一个多类问题实例,让我们来理解数独图像。OCR(Optical Character Recognition,光学字符识别)是一个理解手写或机写文本图像的处理过程。一个常见的例子是通过扫描文件来提取文本,例如书信中的邮政编码或者谷歌图书(http://books.google.com/)里图书馆卷的页数。这里我们看一个简单的在打印的数独图形中识别数字的OCR 问题。数独是一种数字逻辑游戏,规则是用数字 1~9 填满 9×9 的网格,使每一行每一列和每个 3×3 的子网格包含数字 1...91 。在这个例子中我们只对正确地读取和理解它们感兴趣,对于完成识别后怎样求解这些数独问题我们就留给你。
8.4.1 训练分类器
对于这种分类问题,我们有 10 个类:数字 1...9,以及一些什么也没有的单元格。我们给定什么也没有的单元格的类标号是 0,这样所有类标记就是 0...9。我们会用已经剪切好的数独单元格数据集来训练一个 10 类的分类器 2 文件 sudoku_images.zip中有两个文件夹"ocr data"和"sudokus",后者包含了不同条件下的数独图像集,我们稍后讲解。现在我们主要来看文件夹"ocr_data",这个文件夹包含了两个子文件夹,一个装有训练图像,另一个装有测试图像。这些图像文件名的第一个字母是数字(0...9),用以标明它们属于哪类。图 8-6 展示了训练集中的一些样本。图像是灰度图,大概是 80×80 像素(有一幅波动)。
8.4.2 选取特征
我们首先要确定选取怎样的特征向量来表示每一个单元格里的图像。有很多不错的选择;这里我们将会用某些简单而有效的特征。输入一个图像,下面的函数将返回一个拉成一组数组后的灰度值特征向量:
def compute_feature(im):
""" 对一个 ocr 图像块返回一个特征向量 """
调整大小,并去除边界
norm_im = imresize(im,(30,30))
norm_im = norm_im[3:-3,3:-3]
return norm_im.flatten()
compute_feature() 函数用到 imtools 模块中的尺寸调整函数 imresize(),来减少特征向量的长度。我们还修剪掉了大约 10% 的边界像素,因为这些修剪掉的部分通常是网格线的边缘部分,如图 8-6 所示。

8-6:用于训练 10 类数独 OCR 分类器的训练样本图像
现在我们用下面的函数来读取训练数据:
def load_ocr_data(path):
""" 返回路径中所有图像的标记及 OCR 特征 """
对以 .jpg 为后缀的所有文件创建一个列表
imlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.jpg')]
创建标记
labels = [int(imfile.split('/')[-1][0]) for imfile in imlist]
从图像中创建特征
features = []
for imname in imlist:
im = array(Image.open(imname).convert('L'))
features.append(compute_feature(im))
return array(features),labels
上述代码将每一个 JPEG 文件的文件名中的第一个字母提取出来做类标记,并且这些标记被作为整型数据存储在 lables 列表里;用上面的函数计算出的特征向量存储在一个数组里。
8.4.3 多类支持向量机
在得到了训练数据之后,我们接下来要学习一个分类器,这里将使用多类支持向量机。代码和上一节中的代码类似:
from svmutil import *
训练数据
features,labels = load_ocr_data('training/')
测试数据
test_features,test_labels = load_ocr_data('testing/')
训练一个线性 SVM 分类器
#将 features 和 test_features 转换为列表格式
features = map(list,features)
test_features = map(list,test_features)
#创建一个 SVM 问题对象 prob,包含标签 labels 和特征 features。
#这里的 list(features) 确保特征数据是列表格式。
prob = svm_problem(labels,features)
#创建一个 SVM 参数对象 param,指定使用线性核(-t 0)
param = svm_parameter('-t 0')
m = svm_train(prob,param)
在训练数据上分类效果如何
res = svm_predict(labels,features,m)
在测试集上表现如何
res = svm_predict(test_labels,test_features,m)
m = svm_train(prob,param)
在训练数据上分类效果如何
res = svm_predict(labels,features,m)
在测试集上表现如何
res = svm_predict(test_labels,test_features,m)
该代码会训练出一个线性 SVM 分类器,并在测试集上对该分类器的性能进行测试,你可以通过调用最后两个 svm_predict() 函数得到以下输出结果:
Accuracy = 100% (1409/1409) (classification)
Accuracy = 99.2979% (990/997) (classification)
真是一个极好的结果,训练集中的 1409 张图像在 10 类中都被完美地分准确了,在测试集上识别性能也在 99% 左右。现在我们可以将这一分类器用到经过裁剪的新数独图像上。
8.4.4 提取单元格并识别字符
有了识别单元格内容的分类器后,下一步就是自动地找到这些单元格。一旦我们解决了这个问题,就可以对单元格进行裁剪,并把裁剪后的单元格传给分类器。我们假设数独图像是已经对齐的,其水平和垂直网格线平行于图像的边,如图 8-7 所示。在这些条件下,我们可以对图像进行阈值化处理,并在水平和垂直方向上分别对像素值求和。由于这些经阈值处理的边界值为 1,而其他部分值为 0,所以这些边界处会给出很强的响应,可以告诉我们从何处进行裁剪。
下面函数接受一幅灰度图像和一个方向,返回该方向上的 10 条边界:
from scipy.ndimage import measurements
def find_sudoku_edges(im,axis=0):
""" 对一幅对齐后的数独图像查找单元格的边界 """
阈值处理,处理后对每行(列)相加求和
trim = 1*(im<128)
s = trim.sum(axis=axis)
寻找连通域
s_labels,s_nbr = measurements.label(s>(0.5*max(s)))
计算各连通域的质心
m = measurements.center_of_mass(s,s_labels,range(1,s_nbr+1))
对质心取整,质心即为相线条所在位置
x = [int(x[0]) for x in m]
只要检测到 4 条粗线,便在这 4 条粗线之间添加直线
if len(x)==4:
dx = diff(x)
x = [x[0],x[0]+dx[0]/3,x[0]+2*dx[0]/3,
x[1],x[1]+dx[1]/3,x[1]+2*dx[1]/3,
x[2],x[2]+dx[2]/3,x[2]+2*dx[2]/3,x[3]]
if len(x)==10:
return x
else:
raise RuntimeError('Edges not detected.')
首先对图像进行阈值化处理,对灰度值小于 128 的暗区域赋值为 1,否则为 0;然后在特定的方向上(如 axis=0 或 1)对这些经阈值处理后的像素相加求和。Scipy.ndimage 包含 measurements 模块,该模块在二进制或标记数组中对于计数及测量区域是非常有用的。首先,labels() 找出二进制数组中相连接的部件;该二进制数组是通过求和后取中值并进行阈值化处理得到的。然后,center_of_mass() 函数计算每个独立组件的质心。你可能得到 4 个或 10 个点,这主要依赖于数独平面造型设计(所有的线条是等粗细的或子网格线条比其他的粗)。在 4 个点的情况下,会以一定的间隔插入 6 条直线。如果最后的结果没有 10 条线,则会抛出一个异常。sudokus 文件夹里包含不同难易程度的数独图像,每幅图像都对应一个包含数独真实值的文件,我们可以用它来检查识别结果。有一些图像已经和图像的边框对齐,从中挑选一幅图像,用以检查图像裁剪及分类的性能:
imname = 'sudokus/sudoku18.jpg'
vername = 'sudokus/sudoku18.sud'
im = array(Image.open(imname).convert('L'))
查找单元格边界
x = find_sudoku_edges(im,axis=0)
y = find_sudoku_edges(im,axis=1)
裁剪单元格并分类
crops = []
for col in range(9):
for row in range(9):
crop = im[y[col]:y[col+1],x[row]:x[row+1]]
crops.append(compute_feature(crop))
res = svm_predict(loadtxt(vername),map(list,crops),m)[0]
res_im = array(res).reshape(9,9)
print 'Result:'
print res_im
找到边界后,从每一个单元格提取出 crops。将裁剪出来的这些单元格传给同一特征提取函数,并将提取出来的特征作为训练数据保存在一个数组中。通过 loadtxt()读取数独图像的真实标记,用 svm_predict() 函数对这些特征向量进行分类,在控制台上打印出的结果应该为:
Accuracy = 100% (81/81) (classification)
Result:
\[ 0. 0. 0. 0. 1. 7. 0. 5. 0.
9. 0. 3. 0. 0. 5. 2. 0. 7.
0. 0. 0. 0. 0. 0. 4. 0. 0.
0. 1. 6. 0. 0. 4. 0. 0. 2.
0. 0. 0. 8. 0. 1. 0. 0. 0.
8. 0. 0. 5. 0. 0. 6. 4. 0.
0. 0. 9. 0. 0. 0. 0. 0. 0.
7. 0. 2. 1. 0. 0. 8. 0. 9.
0. 5. 0. 2. 3. 0. 0. 0. 0.\]
这里使用的只是其中较简单的图像,请尝试对一些别的数独图像进行识别,看看识别准确率如何,以及分类器在哪些地方出现识别错误。
如果你用一个 9×9 的子图绘制这些经裁剪后的单元格,它们应该和图 8-7(右图)类似。
图 8-7:一个检测并裁剪这些数独网格区域的例子:一幅数独网格图像 ( 左 );9×9 裁剪后的图像,每个独立单元都会被送到 OCR 分类器中 ( 右 )
8.4.5 图像校正
如果你对上面分类器的性能还算满意,那么下一个挑战便是如何将它应用于那些没有对齐的图像。这里我们将用一种简单的图像校正方法来结束本章数独图像识别的例子,使用该校正方法的前提是网格的 4 个角点都已经被检测到或者手工做过标记。图 8-8(左)中是一幅在进行识别时受角度影响剧烈的图像。
一个单应矩阵可以像上面的例子那样映射网格以使边缘能够对齐,我们这里所要做的就是估算该变换矩阵。下面的例子手工标记 4 个角点,然后将图像变换为一个1000×1000 大小的方形图像:
from scipy import ndimage
import homography
imname = 'sudoku8.jpg'
im = array(Image.open(imname).convert('L'))
标记角点
figure()
imsshow(im)
gray()
x = ginput(4)
左上角、右上角、右下角、左下角
fp = array([array([p[1],p[0],1]) for p in x]).T
tp = array([[0,0,1],[0,1000,1],[1000,1000,1],[1000,0,1]]).T
估算单应矩阵
H = homography.H_from_points(tp,fp)
辅助函数,用于进行几何变换
def warpfcn(x):
x = array([x[0],x[1],1])
xt = dot(H,x)
xt = xt/xt[2]
return xt[0],xt[1]
用全透视变换对图像进行变换
im_g = ndimage.geometric_transform(im,warpfcn,(1000,1000))
3 章中对很多样本图像进行的仿射变换还达不到对这些数独图像进行校正的要求,这里用到了 scipy.ndinmage 模块中一个更加普遍的变换函数 geometric_transform(),该函数获取一个 2D 到 2D 的映射,映射为另一个二维来取代变化矩阵,所以我们需要一个辅助函数(该例中用一个三角形的分段仿射变换),变换后的图像如图 8-8 中右图所示。
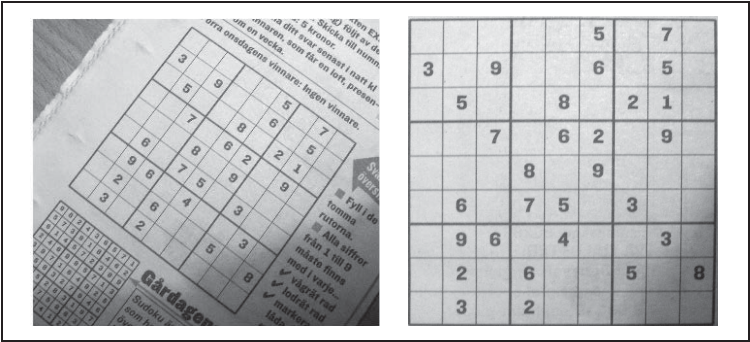
图 8-8:用全透视变换对一幅图像进行校正的例子。四个角点被手工标记的数独原图(左),变换为 1000×1000 大小的方形图(右)