题目描述
有 n 个字母,列出由该字母组成的字符串的全排列(相同的排列只计一次)。
输入格式
第一行输入是字母个数 n 。
接下来一行输入的是待排列的 n 个字母。
输出格式
计算出的 n 个字母的所有不同排列总数。
样例输入输出
样例输入
4
aacc
样例输出
6
数据范围
对于 100% 的数据,保证 1≤n≤201≤n≤20 。
来源/分类(难度系数:二星 )
搜索 排列
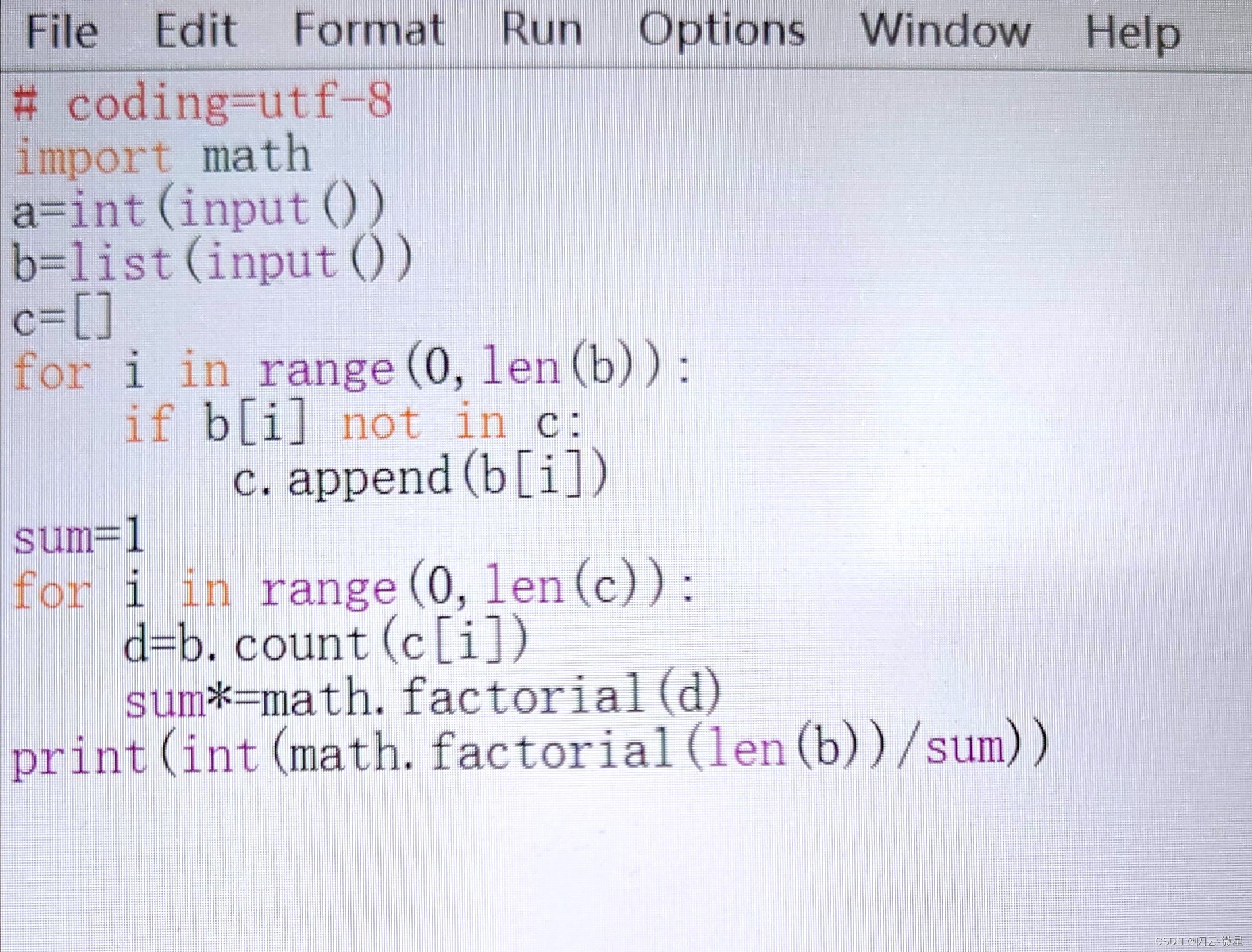
完整代码展示:
import math
a=int(input())
b=list(input())
c=[]
for i in range(0,len(b)):
if b[i] not in c:
c.append(b[i])
sum=1
for i in range(0,len(c)):
d=b.count(c[i])
sum*=math.factorial(d)
print(int(math.factorial(len(b))/sum))
python
import math
a=int(input())
b=list(input())
c=[]
for i in range(0,len(b)):
if b[i] not in c:
c.append(b[i])
sum=1
for i in range(0,len(c)):
d=b.count(c[i])
sum*=math.factorial(d)
print(int(math.factorial(len(b))/sum))代码解释:
"import math ",导入math库。
"a=int(input()) ",导入用户的字符个数a。
"b=list(input()) ",导入用户的字符串,并将该字符串分解为单字符储存在列表b中。
"c=[]
for i in range(0,len(b)):
if b[i] not in c:
c.append(b[i]) ",建立一个空列表c,接着遍历b中元素,判断b[i]是否在c中,如果不在:则将b[i]添加进c中。
"sum=1
for i in range(0,len(c)):
d=b.count(c[i])
sum*=math.factorial(d) ",令sum为1,利用factorial()函数计算b中每种元素的数量的阶乘。接着令sum乘以该阶乘。
"print(int(math.factorial(len(b))/sum)) ",打印列表b长度的阶乘除以sum,并将结果转换为整数型。
数学背景:
排列组合的数学原理主要基于两个基本计数原理:加法原理和乘法原理。这些原理是理解和计算排列组合问题的基础。
加法原理:当完成某件事情存在多种互不重叠的方法时,将每种方法的结果相加即得到总的方法数。例如,从A地到B地,可以选择火车、汽车或飞机,每种交通方式各有不同的方法数,因此总的方法数是这几种交通方式方法数的和。
乘法原理:当完成某件事情需要多个步骤,每个步骤又有多种方法时,将每个步骤的方法数相乘即得到总的方法数。例如,从A地到B地,如果需要先从A地到C地,再从C地到B地,那么从A地到B地的方法数是这两个步骤方法数的乘积。
排列(permutation)和组合(combination)是两种基本的排列组合类型,它们在数学和日常生活中都有广泛的应用。
排列:从n个不同元素中取出m个元素(m≤n),按照一定的顺序排成一列,称为从n个元素中取出m个元素的排列。排列种数记作 P(n,m)P(n, m)P(n,m) 。例如,从1到5这五个数字中取出3个数字,按照从小到大的顺序排列,共有6种排列方式。
组合:从n个不同元素中取出m个元素(m≤n),不考虑元素的顺序,称为从n个元素中取出m个元素的组合。组合种数记作 C(n,m)C(n, m)C(n,m) 。例如,从1到5这五个数字中取出3个数字,不考虑顺序,共有10种组合方式。
计算公式:
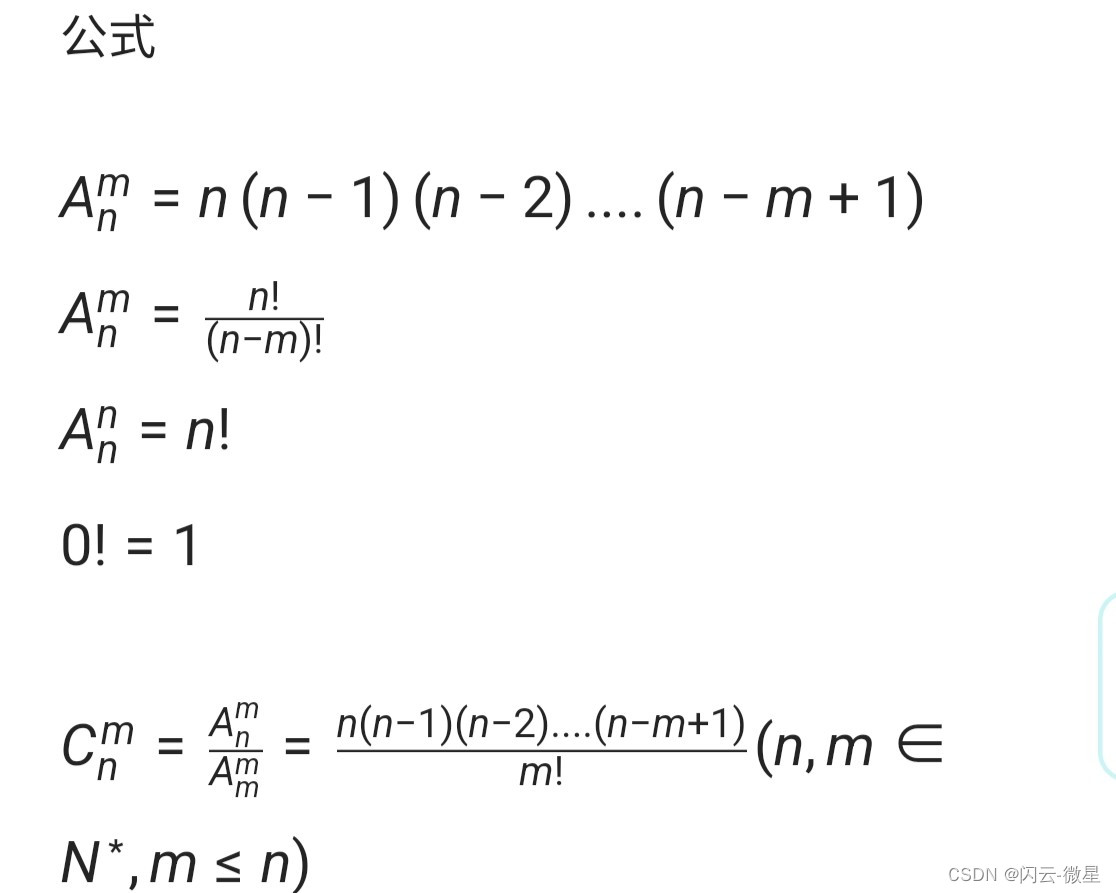
运行效果展示:

(声明:以上内容均为原创)