一、ATA
任给一个矩阵A,都有: ATA 为一个对称矩阵
例子:A为一个m×n的矩阵,A的转置为一个n×m的矩阵
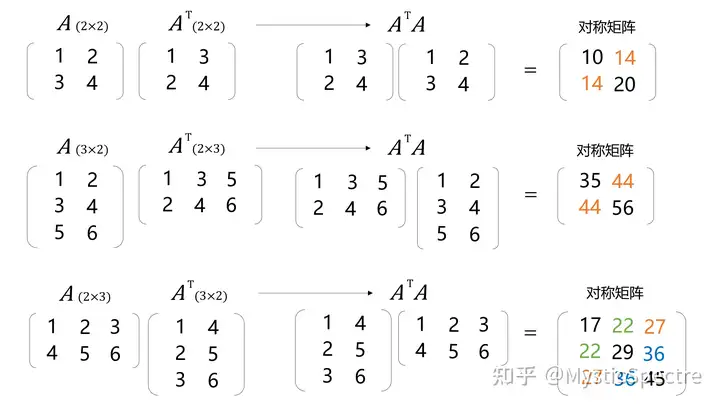
对称矩阵的重要性质如下:
① 对称矩阵的特征值全为实数(实数特征根)
② 任意一个n阶对称矩阵,一定有代数重数=几何重数
若对称矩阵A的某个特征值的重数=k,则对应的几何重数=k
即一个特征根的重数若为k,则:
该特征根可找到对应线性无关的特征向量个数一定也为k
③ 任意一个n阶对称矩阵,一定有n个线性无关的特征值向量
如果无重根,即n个特征值对应n个线性无关的特征向量
倘若有k重根,也该重根必有k个线性无关的特征向量
倘若有k个重根,可理解为k个相同的特征值而已(总的特征值个数还是n)
也就是:一定有n个特征值,一定有n个线性无关的特征值向量
④ 任意一个n阶对称矩阵,一定能相似对角化
任意一个n阶对称矩阵,一定有n个线性无关的特征值向量
所以对称矩阵一定满足对角化条件,即:
任意一个n阶对称矩阵A,都有 A=PDP−1
任意一个n阶对称矩阵A,都有相似矩阵为对角矩阵的矩阵
对角矩阵D上,主对角线上的元素即为A或D的特征值
⑤ 任意一个n阶对称矩阵,一定能正交对角化
不同特征值对应的特征向量是彼此正交的
彼此正交是指:两个向量的乘积=0,即两个向量相互垂直
也就是: A=PDP−1 中的 P 为正交矩阵
二、ATA 的特征值与奇异值
由于 ATA 相乘后得到的一定是一个对称矩阵(n×n)
那么 ATA 一定有:
n个实数特征值,记为: λ1,λ2,...,λn
n个线性无关的特征向量,记为: v1→,v2→,...,vn→
也就是: v1→,v2→,...,vn→ 为n个相互垂直的特征向量
那么此时称: λi 为 ATA 的奇异值
记作: σi=λi
三、ATA 奇异值的非负性
结论:ATA的特征值 λi≥0
从而可得:ATA的奇异值 λi≥0
即: σi≥0
推导过程如下:
矩阵A左乘特征向量 vi→ 得到一个新的向量
那么这个新的向量模的平方记为: ||Avi→||2
因为两个相同的向量点乘就等于该向量模的平方
a→·a→=||a→||×||a→||×cos(0)=||a→||×||a→||×1=||a→||2
那么: ||Avi→||2=(Avi→)(Avi→)
将两个向量的点乘转为两个矩阵相乘,即为:
(Avi→)(Avi→)=(Avi)T(Avi)
将转置打开得: (Avi)T(Avi)=viTATAvi
由矩阵乘法结合律可得: viTATAvi=viT(ATAvi)
特征值的定义为: Axi→=λxi→
因为 ATA 的特征值为: λi
于是: ATAvi=λivi
从而: viT(ATAvi)=viTλivi
因为: λi 为一个常数,满足矩阵乘法交换律
于是: viTλivi=λiviTvi
接着: viTvi 转为两个向量的点乘 vi→·vi→=||vi||2
那么: λiviTvi=λi||vi||2
此时我们将:特征向量进行归一化处理
也就是将:v1→,v2→,...,vn→ 转为n个相互垂直的单位特征向量
记为: u1→,u2→,..,un→
那么将 vi 替换成 ui 后为: λi||ui||2
因为: ui 为相互垂直的单位特征向量
所以:每个 ui 的模长为1,于是: ||ui||2=1
那么: λi||ui||2=λi
最终: ||Avi→||2=λi
由于: ||Avi→||2 为非负数(一个向量的模长的平方为非负数)
所以: λi 也为非负数,即 λi≥0
四、换个角度看ATA的奇异值
由上面可知: σi=λi=||Avi→||2=||Avi→||
那么可以说:奇异值 σi 就是这个向量 Avi→ 的模长
也可以说:矩阵A左乘 ATA 特征向量 vi 后
得到该新向量的模长 (||Avi→||) 即为 ATA 的奇异值