二叉树最小深度

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

复制代码

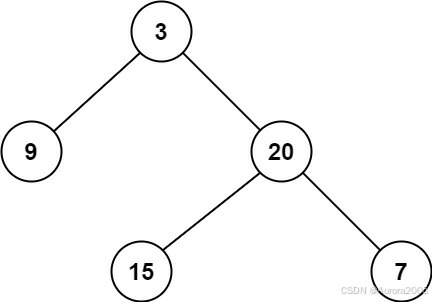
Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

复制代码

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Constraints:

The number of nodes in the tree is in the range [0, 105].
-1000 <= Node.val <= 1000

递归：

后序：

class Solution {
public:
    int getDepth(TreeNode*node){
        if(node==NULL)return 0;
        int leftDepth=getDepth(node->left);
        int rightDepth=getDepth(node->right);

        if(node->left==NULL && node->right!=NULL){
            return 1+rightDepth;
        }
        if(node->left!=NULL && node->right==NULL){
            return 1+leftDepth;
        }

        int result=1+min(leftDepth,rightDepth);
        return result;
    }
    int minDepth(TreeNode* root) {
        return getDepth(root);
    }
};

思路：

1，最小深度需要在中间加上判断左右子树是否一个为空，一个不为空，因为最小深度是指到叶节点的最小深度

2，记得加1

前序：

class Solution {
public:
    int result;
    void getDepth(TreeNode*node,int depth){
        if(node==NULL)return;

        if(node->left==NULL && node->right==NULL){
            result=min(result,depth);
        }
        if(node->left){
            getDepth(node->left,depth+1);
        }
        if(node->right){
            getDepth(node->right,depth+1);
        }
        
        return;
    }
    int minDepth(TreeNode* root) {
        if(root==NULL)return 0;
        result=INT_MAX;
        getDepth(root,1);
        return result;
    }
};

思路：

1，中（result=min（result，depth））左（递归）右（递归），找到最后没有左右子树的叶节点。

2，递归回去时，Depth+1

迭代法：

class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==NULL)return 0;
        int depth=0;
        queue<TreeNode*>que;
        que.push(root);
        while(!que.empty()){
            int size=que.size();
            depth++;
            for(int i=0;i<size;i++){
                TreeNode*node=que.front();
                que.pop();
                if(node->left)que.push(node->left);
                if(node->right)que.push(node->right);
                if(node->left==NULL && node->right==NULL)return depth;
            }
        }
        return depth;
    }
};

思路：

1，别忘了每一层遍历depth++

2，TreeNode*node=que.front();

que.pop();这两行代码需要再for循环中用，这样，每次下一层遍历的时候都能刚好把上一层的pop掉