参考：【PCL】------ 点云配准ICP(Iterative Closest Point)算法_icp点云配准-CSDN博客
点云配准
计算出两个点云簇之间的变换矩阵，从而计算出位姿等信息，学习点云配准的目的是想要计算相邻两帧物体的点云之间的变换位姿，从而得到物体的运动信息。
ICP算法
ICP即 Iterative Closest Point 迭代最近点法，是一种经典的点云配准方法。ICP算法需要输入两个点云，一个是目标点云，另一个是源点云，输出的是从源点云到目标点云的位姿变换。目标点云 不会移动，而源点云则会在迭代的过程中不断接近目标点云，直到收敛。
但是ICP算法很容易陷入局部最优解，通常需要目标点云和源点云在配准前有比较高的重合率，因此在执行ICP之前通常会用其他方法进行一次粗配准，来获得比较好的初值，然后再使用ICP进行精配准。
原理推导
对于给定的点集 P = {P1, P2, P3, ... , Pn} 和 点云 Q = {qi, q2, q3, ... , qn}， 经典的ICP算法会对以下目标函数进行优化
该目标函数的含义也比较好理解，即找到一个刚体变换 < R, t > 使得源点云 P 和 目标点云 Q 的 差异尽可能的小，那么如何衡量这两个点云簇的差异呢？经典的ICP算法会遍历 < R, t > 变换后的源点云中的所有点 ，从目标点云中搜索出每一个
的最近邻点
，形成点对
，计算点对距离的平方，并对所有点对的距离平方求和，最和最小则认为差异最小。
当匹配点对确定好之后，ICP的优化函数其实是一个凸函数，可以找到最优解，求解过程可以使用SVD分解，具体过程略
基于PCL的ICP代码详解
PCL点云库已经实现了多种点云配准算法，结合pcl，本次配准的主要目的是：
- 对PCL中ICP算法进行一些注解
- 创建可视化窗口，通过设置键盘回调函数，控制迭代过程，观察ICP算法的计算过程
PCL中的ICP算法是基于SVD（Singular Value Decomposition）实现的.
PCL中ICP的官方参考文档 http://pointclouds.org/docume...
ICP代码参数设置
使用pcl的ICP之前要设置几个参数
cpp
//创建ICP的实例类
pcl::IterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> icp;
// 设置源点云
icp.setInputSource(cloud_sources);
// 设置目标点云
icp.setInputTarget(cloud_target);
// 设置对应点对之间的最大距离，影响结果的精度
icp.setMaxCorrespondenceDistance(100);
// 设置两次变化矩阵之间的差值（一般设置为1e-10即可）
icp.setTransformationEpsilon(1e-10);
// 设置收敛条件是均方误差和小于阈值， 停止迭代
icp.setEuclideanFitnessEpsilon(0.001);
// 设置最大迭代次数
icp.setMaximumIterations(100);
icc.align(final);完整代码
ICP变种之点线PL-ICP
参考：https://zhuanlan.zhihu.com/p/506823350#:~:text=CP%E7%AE%97%E6%B3%95.%20%E5%AF%B9%E4%BA%8Epo
代码：
上述介绍的ICP算法特指 点到点的ICP，即 point-to-point ICP，但是点到点的ICP算存在以下缺点：
- 依赖初始值，初始值不好时，迭代次数增加；
- 对于较大的初始误差，可能会出现错误的迭代结果；
- ICP是一阶收敛，收敛速度慢（为了弥补这一点，通常使用K-D树加快搜索）；
- 存在离群点及噪声。
为此改善上述缺点，有研究者提出了PL-ICP，顾名思义，这种方式使用源点云到目标点云直线的距离度量来估计变换。主要区别在于误差函数的构建上。ICP是找最近邻的一点，以点与点之间的距离作为误差，而PLICP是找到最近邻的两点，两点连线，是以点到线的距离作为误差，实际上，后者的误差度量方式更符合结构化场景中的雷达点云的实际情况。因此具有更小的误差（图2）。然而，它对非常大的初始位移误差的鲁棒性较差，因此需要比较精确的初始值。
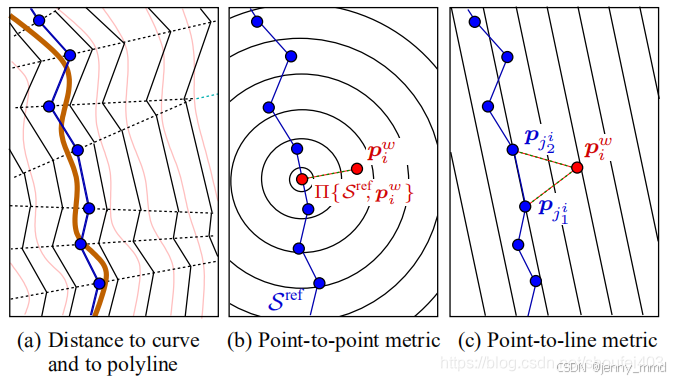图2 点到线度量比普通 ICP 中使用的点到点度量更接近表面的距离
点到线的误差函数写为：
为目标点云中匹配到的最近两个点对应直线的法线。