一、平面及其方程(3个条件,4种表达)
F ( x , y , z ) F(x,y,z) F(x,y,z)为平面方程:
- 在这个平面上的点满足 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0
- 不在这个平面上的点不满足 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0
归根结底,就是要三个点。变化有很多,可能是三个平面内的点,也可能是截点,也可能连成平面内线段后确定法向搞点法式
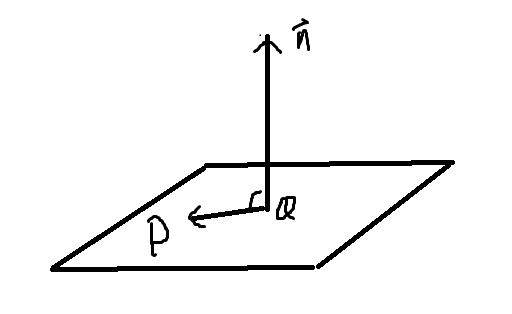
1.点法式
用平面法线和平面上的一个向量来确定平面。
平面方程: a ( x 0 − x ) + b ( y 0 − y ) + c ( z 0 − z ) = 0 a(x_0-x)+b(y_0-y)+c(z_0-z)=0 a(x0−x)+b(y0−y)+c(z0−z)=0
P Q ⋅ n = 0 \mathbf{PQ}\cdot \mathbf n=0 PQ⋅n=0
- 法线 n = ( a , b , c ) \mathbf{n}=(a,b,c) n=(a,b,c)
- 法线和平面交点 Q = ( x 0 , y 0 , z 0 ) Q=(x_0,y_0,z_0) Q=(x0,y0,z0)
- 平面上其他一点 P = ( x , y , z ) P=(x,y,z) P=(x,y,z)
- P Q = ( x 0 − x , y 0 − y , z 0 − z ) \mathbf{PQ}=(x_0-x,y_0-y,z_0-z) PQ=(x0−x,y0−y,z0−z)
2.一般式
A x + B y + C z + D = 0 Ax+By+Cz+D=0 Ax+By+Cz+D=0
3.三点式
用平面上不共线的三点确定一个平面。
已知: A ( x 1 , y 1 , z 1 ) , B ( x 2 , y 2 , z 2 ) , C ( x 3 , y 3 , z 3 ) A(x_1,y_1,z_1),B(x_2,y_2,z_2),C(x_3,y_3,z_3) A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3),在平面上任取一点 P ( x , y , z ) P(x,y,z) P(x,y,z)
P A = ( x 1 − x , y 1 − y , z 1 − z ) \mathbf{PA}=(x_1-x,y_1-y,z_1-z) PA=(x1−x,y1−y,z1−z)
A B = ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 ) \mathbf{AB}=(x_2-x_1,y_2-y_1,z_2-z_1) AB=(x2−x1,y2−y1,z2−z1)
A C = ( x 3 − x 1 , y 3 − y 1 , z 3 − z 1 ) \mathbf{AC}=(x_3-x_1,y_3-y_1,z_3-z_1) AC=(x3−x1,y3−y1,z3−z1)
P A , A B , A C \] = 0 \[\\mathbf{PA},\\mathbf{AB},\\mathbf{AC}\]=0 \[PA,AB,AC\]=0 ( x 1 − x y 1 − y z 1 − z x 2 − x 1 y 2 − y 1 z 2 − z 1 x 3 − x 1 y 3 − y 1 z 3 − z 1 ) = 0 \\left(\\begin{array}{l} x_1-x\&y_1-y\&z_1-z\\\\ x_2-x_1\&y_2-y_1\&z_2-z_1\\\\ x_3-x_1\&y_3-y_1\&z_3-z_1 \\end{array} \\right)=0 x1−xx2−x1x3−x1y1−yy2−y1y3−y1z1−zz2−z1z3−z1 =0 也可以直接根据 A B × A C \\mathbf{AB}\\times\\mathbf{AC} AB×AC构造法向量,然后用点法式。 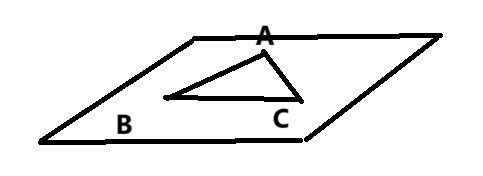 #### 4.截距式 若平面和三坐标轴分别相交于A(a,0,0),B(0,b,0),C(0,0,c),则从上面的三点式可以得: ( a − x − y − z − a b 0 − a 0 c ) = 0 b c x + a c y + a b z = a b c x a + y b + z c = 1 \\left(\\begin{array}{l} a-x\&-y\&-z\\\\ -a\&b\&0\\\\ -a\&0\&c \\end{array} \\right)=0 \\\\ bcx+acy+abz=abc\\\\ \\frac xa+\\frac yb+\\frac zc=1 a−x−a−a−yb0−z0c =0bcx+acy+abz=abcax+by+cz=1 对于一般式: A x + B y + C z = D Ax+By+Cz=D Ax+By+Cz=D =\> A D x + B D y + C D z = 1 \\frac ADx+\\frac BDy+\\frac CDz=1 DAx+DBy+DCz=1 A D = 1 a ; B D = 1 b ; C D = 1 c \\frac AD=\\frac 1a;\\frac BD=\\frac 1b;\\frac CD=\\frac1c DA=a1;DB=b1;DC=c1 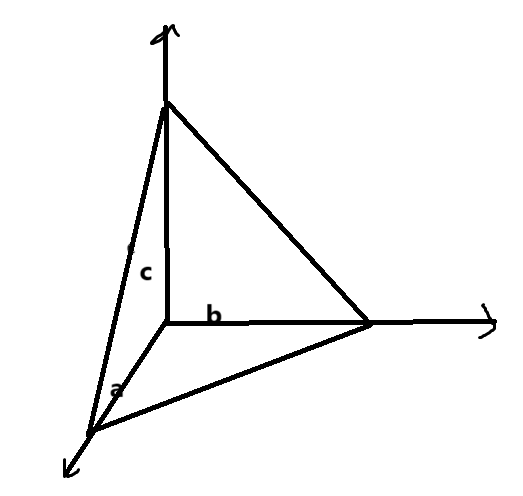 ### 二、平面和平面的关系 假设有两个平面,平面方程分别为 A 1 x + B 1 y + C 1 z + D 1 = 0 , A 2 x + B 2 y + C 2 z + D 2 = 0 A_1x+B_1y+C_1z+D_1=0,A_2x+B_2y+C_2z+D_2=0 A1x+B1y+C1z+D1=0,A2x+B2y+C2z+D2=0 #### 1.垂直 两平面垂直的时候两平面对应法向量也垂直。 n 1 ⋅ n 2 = 0 \\mathbf{n_1}\\cdot \\mathbf{n_2}=0 n1⋅n2=0 #### 2.平行(不重叠) n 1 / / n 2 \\mathbf{n_1}//\\mathbf{n_2} n1//n2 * n 1 = k n 2 ( k ≠ 0 ) \\mathbf{n_1}=k\\mathbf{n_2}(k\\ne 0) n1=kn2(k=0) * n 1 × n 2 = 0 \\mathbf{n_1}\\times\\mathbf{n_2}=0 n1×n2=0 * A 1 A 2 = B 1 B 2 = C 1 C 2 = λ , D 1 D 2 ≠ λ \\frac{A_1}{A_2}=\\frac{B_1}{B_2}=\\frac{C_1}{C_2}=\\lambda,\\frac{D_1}{D_2}\\ne \\lambda A2A1=B2B1=C2C1=λ,D2D1=λ #### 3.重叠 n 1 = n 2 \\mathbf{n_1}=\\mathbf{n_2} n1=n2 * n 1 = k n 2 \\mathbf{n_1}=k\\mathbf{n_2} n1=kn2 * A 1 A 2 = B 1 B 2 = C 1 C 2 = D 1 D 2 = λ \\frac{A_1}{A_2}=\\frac{B_1}{B_2}=\\frac{C_1}{C_2}=\\frac{D_1}{D_2}=\\lambda A2A1=B2B1=C2C1=D2D1=λ #### 4.相交 不平行,可能垂直的状态。 * n 1 ≠ k n 2 \\mathbf{n_1}\\ne k\\mathbf{n_2} n1=kn2 * n 1 × n 2 ≠ 0 \\mathbf{n_1}\\times\\mathbf{n_2}\\ne0 n1×n2=0