质点的角动量
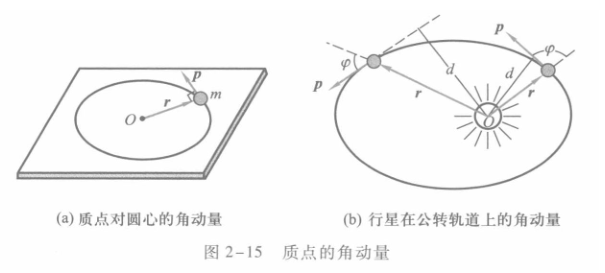
角动量是矢量,可用位矢和动量的矢积表示:
\[\vec{L} = \vec{r} \times \vec{p} \tag{1} \]
惯性张量
对于通过质心,绕任意轴以角速度\(\omega\)旋转的刚体,对于质心的角动量定义为:
\[H_{cg} = \int(\vec{r} \times (\vec{\omega} \times \vec{r})) dm \]
r和w可以写成向量:
\[\vec{r} = x\vec{i} + y\vec{j} + z\vec{z} \]
\[\vec{\omega} = \omega_x\vec{i} + \omega_y\vec{j} + \omega_z\vec{z} \]
向量叉乘可以写成矩阵和向量相乘的形式:
\[\vec{r} \times \vec{q} = \begin{bmatrix} r_y q_z - r_z q_y \\ r_z q_x - r_x q_z \\ r_x q_y -r_y q_x \end{bmatrix} = \begin{bmatrix} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{bmatrix} \begin{bmatrix} q_x \\ q_y \\ q_z \end{bmatrix} \]
因此展开角动量公式里的叉乘:
\[H_{cg} = \int(\vec{r} \times (\vec{\omega} \times \vec{r})) dm = \int( \begin{bmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{bmatrix} \begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} ) dm \\ = \int( \begin{bmatrix} -z\omega_z-y\omega_y & y\omega_x & z\omega_x \\ x\omega_y & -z\omega_z-x\omega_x & z\omega_y \\ x\omega_z & y\omega_z & -y\omega_y-x\omega_x \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} ) dm \\ = \int( \begin{bmatrix} (y^2+z^2)\omega_x-xz\omega_z - xy\omega_y \\ (x^2+z^2)\omega_y -yz\omega_z-xy\omega_x \\ (x^2+y^2)\omega_z - yz\omega_y - xz\omega_x \end{bmatrix} ) dm \\ \]
令:
\[I_{xx} = \int(y^2+z^2)dm \]
\[I_{yy} = \int(x^2+z^2)dm \]
\[I_{zz} = \int(y^2+x^2)dm \]
\[I_{xy} = I_{yx} = \int(xy)dm \]
\[I_{xz} = I_{zx} = \int(xz)dm \]
\[I_{yz} = I_{zy} = \int(yz)dm \]
上式可改写为:
\[H_{cg} = \begin{bmatrix} I_{xx}\omega_x-I_{xz}\omega_z - I_{xy}\omega_y \\ I_{yy}\omega_y -I_{yz}\omega_z-I_{xy}\omega_x \\ I_{zz}\omega_z -I_{yz}\omega_y - I_{xz}\omega_x \end{bmatrix} \\ = \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \\ \end{bmatrix} \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \]
令矩阵I:
\[I = \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \\ \end{bmatrix} \]
最终得到:
\[H_{cg} = I\vec{\omega} \]
I就是转动惯量。
上式两边对于时间求导,在极短的时间内可以认为惯性矩阵I是常量:
\[\frac{d H_{cg}}{dt} = I \frac{d \vec{\omega}}{dt} = I \vec{\alpha} \]
根据角动量定理(总外力矩等于刚体角动量的时间变化率),左侧就是外力矩,因此:
\[\vec{M} = I \vec{\alpha} \Rightarrow I^{-1} \vec{M} = \vec{\alpha} \tag{6} \]
这是旋转的运动学公式,总外力矩克服转动惯量,给予物体于角加速度。
和平移运动公式\(\vec{F}=m\vec{a}\)具有一样结构和地位。
计算转动惯量
\[I_{xx} = \int(y^2+z^2)dm \]
\[I_{yy} = \int(x^2+z^2)dm \]
\[I_{zz} = \int(y^2+x^2)dm \]
\[I_{xy} = I_{yx} = \int(xy)dm \]
\[I_{xz} = I_{zx} = \int(xz)dm \]
\[I_{yz} = I_{zy} = \int(yz)dm \]
\[I = \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xz} & -I_{yz} & I_{zz} \\ \end{bmatrix} \]
根据它的定义,坐标系恒定情况下,当物体姿态发生变化后,各个质量微原的位置发生了变化,因此每个量都需要重新计算,这带来了很大计算量。
然而实际不需要那么麻烦。
将I写成另一种形式:
\[I=\sum m_i(r_i^T r_i 1 - r_i r_i^T) \]
其中 1代表单位矩阵。
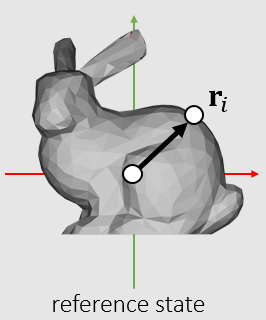
如图在参考姿态下:
\[I_{ref}=\sum m_i(r_i^T r_i 1 - r_i r_i^T) \]
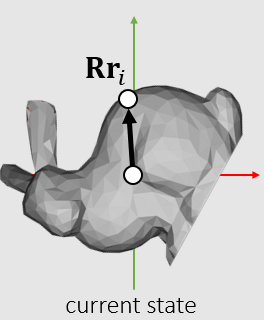
当物体旋转后,原来的微原位于\(Rr_i\)处,因此
\[I=\sum m_i((Rr_i)^T (Rr_i) 1 - (Rr_i) (Rr_i)^T) \\ =\sum m_i(r_i^T R^T Rr_i 1 - Rr_i r_i^T R^T) \\ =\sum m_i(r_i^T r_i 1 - Rr_i r_i^T R^T) \\ =\sum m_i(R r_i^T r_i 1 R^T - Rr_i r_i^T R^T) \\ =\sum m_i R(r_i^T r_i 1 - r_i r_i^T) R^T \\ =R I_{ref} R^T \]
最后:
\[I = R I_{ref} R^T \]