数据结构与算法基础篇

数据结构基本概念

数据（data）

是描述客观事物的数值、字符以及能输入机器且能被处理的各种符号集合

数据元素（data element）

是数据的基本单位，是数据集合的个体，在计算机程序中通常作为一个整体来进行处理

数据对象（data object）

是性质相同的数据元素的集合，是数据的子集

数据结构（data structure）

是指相互之间存在一种或多种特定关系的数据元素的集合。是组织并存储数据以便能够有效使用的一种专门格式，它用来反映一个数据的内部构成，即一个数据由那些成分数据构成，以什么方式构成，呈什么结构。表示一组数据元素及其相互关系的数据结构同样也有两种不同的表现形式，一种是数据结构的逻辑层面，即数据的逻辑结构 ；一种是存在于计算机世界的物理层面，即数据的存储结构。

数据逻辑结构

数据的逻辑结构按照数据元素之间相互关系的特性来分，可以分为以下四种结构：集合、线性结构、树形结构和图状结构。

线性结构 线性表、栈、队列属于线性结构。非线性结构树和图

逻辑结构的表现形式：

go 复制代码

数据结构 = {D , S}

其中D 是数据元素的集合；S 是D 中数据元素之间的关系集合，并且数据元素之间的关系是使用序偶来表示的。序偶是由两个元素x 和y 按一定顺序排列而成的二元组，记作 <x , y>，x 是它的第一元素，y 是它的第二元素。集合结构表达：

go 复制代码

K = {01, 02, 03, 04, 05}
R = {}

线性结构

go 复制代码

K = {01, 02, 03, 04, 05}
R = {<02,04>, <03,05>, <05,02>, <01,03>}

树

go 复制代码

K = {01, 02, 03, 04, 05, 06}
R = {<01,02>, <01,03>, <02,04>, <02,05>, <03,06>}

图

go 复制代码

K = {01, 02, 03, 04, 05}
R = {<01,02>, <01,05>, <02,01>, <02,03>, <02,04>, <03,02>,
<04,02>, <04,05>, <05,01>, <05,04>}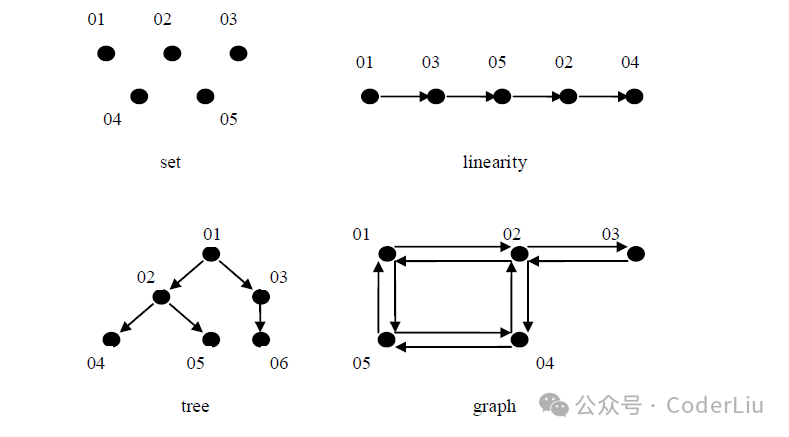

顺序存储结构的特点

数据元素的存储对应于一块连续的存储空间，数据元素之间的前驱和后续关系通过数据元素在存储器中的相对位置来反映。

链式存储结构的特点：

数据元素的存储对应的是不连续的存储空间，每个存储节点对应一个需要存储的数据元素。元素之间的逻辑关系通过存储节点之间的链接关系反映出来。

算法以及性能

算法

❝

算法（algorithm）是指令的集合，是为解决特定问题而规定的一系列操作。它是明确定义的可计算过程，以一个数据集合作为输入，并产生一个数据集合作为输出。算法的五大特性

输入：一个算法应以待解决的问题的信息作为输入。
输出：输入对应指令集处理后得到的信息
可行性：算法是可行的，即算法中的每一条指令都是可以实现的，均能在有限的时间内完成。
有穷性：算法执行的指令个数是有限的，每个指令又是在有限时间内完成的，因此整个算法也是在有限时间内可以结束的。
确定性：算法对于特定的合法输入，其对应的输出是唯一的。即当算法从一个特定输入开始，多次执行同一指令集结果总是相同的。

时间复杂性

❝

算法的时间复杂度是用来衡量算法执行效率的一个重要指标，它描述的是算法运行时间与输入数据规模之间的增长关系。计算时间复杂度通常采用大O符号（Big O notation）来表示。

**基本操作：**在分析时间复杂度时，我们关注的是算法中最基本的操作次数。基本操作是指那些无论对于何种输入规模，其执行时间都是常数的操作，如赋值、比较、算术运算等。
最坏情况下的时间复杂度：通常情况下，我们关心的是算法在最坏情况下的时间复杂度，即输入数据以最不利于算法的方式排列时，算法所需的最大运行时间。
常见的时间复杂度：O(1)：常数时间复杂度，表示算法执行时间不受输入规模影响。O(logn)：对数时间复杂度，常见于二分查找等算法。O(n)：线性时间复杂度，表示算法执行时间与输入规模成正比。O(nlogn)：常见于高效的排序算法，如快速排序、归并排序。O(n^2)：平方时间复杂度，常见于嵌套循环结构，如冒泡排序、选择排序。O(2^n)：指数时间复杂度，常见于递归求解组合问题的情况。O(n!)：阶乘时间复杂度，常见于全排列等问题。
**计算步骤：**1.确定基本操作。2.分析基本操作随着输入规模的变化趋势。3.使用大O符号表示这个变化趋势。4.简化规则：只保留最高次项：如果一个算法的时间复杂度为 O(3n^2 + 5n + 7)，则简化为 O(n^2)。去掉系数：如 O(2n) 简化为 O(n)

举例：选择排序算法

go 复制代码

/**
 * 选择排序算法
 */
public class SelectSort {
    public static void main(String[] args) {
        int[] a = {1,9, 8, 4, 5, 7, 6, 10, 9};
        SelectSort selectSort = new SelectSort();
        selectSort.Sort(a);
        for (int i : a) {
            System.out.print(i+" ");
        }
    }
    /**
     * 选择排序算法
     * @param a
     */
    public void Sort (int[] a) {
        int n = a.length;
        for (int k=0; k<n-1; k++) {
            int min = k;
            for (int i=k+1; i<n; i++) {
                if (a[i]<a[min]) {
                    min = i;
                }
            }
            if (k!=min){
                int temp = a[k];
                a[k] = a[min];
                a[min] = temp;
            }
        }
    }

n个元素，

第一趟排序(降序)需要找出最小的数放在第一位
第二趟排序找出第二次最小数的放在第二位
....
直到倒数第二个数和最后一个数比较大小

go 复制代码

双重循环：
第一次循环操作比较n-1次
第二次循环操作比较n-2次
...
最后一次比较操作1次
最终的表达式为：(n-1)+(n-2)+...+1
等差数列求和：(首项+尾项)*项数/2=((n-1)+1)*(n-1)/2=(n*(n-1))/2

保留最高项：简化为 O(n^2)