在许多游戏和应用程序中,优秀的用户交互设计是至关重要的,它能够让用户感受到与现实世界中物体的互动,即便他们实际上只是在与屏幕上的像素进行交互。而在安卓上则主要以触控交互为主。本篇我们将探讨如何通过添加触控功能来增强一个场景的交互性。我们将学习三维空间中的碰撞检测和交互技术,使得我们能够在屏幕上拖动圆柱体的。
本篇的开发计划包括以下几个步骤:
-
首先,我们将继续从上一篇的项目开始,添加触控交互功能。我们会回顾一些必要的数学知识,这些是实现交互功能的基础。
-
接着,我们将探索如何让两个圆柱体进行互动,并确保它们在游戏边界内移动。
本篇之后,我们将能够使用圆柱体进行相互碰撞,并观察它在桌面上反弹的效果。
添加触控
首先我们现在许久未动的Activity中添加如下代码:
var renderer:TouchRenderer = TouchRenderer(this)
glSurfaceView.setOnTouchListener { v, event ->
glSurfaceView.queueEvent{
var x = (event.x-v.width/2)/(v.width/2)
var y = -1*(event.y-v.height/2)/(v.height/2)
event.setLocation(x,y)
renderer.onTouchEvent(event)
}
true
}在Android系统中,我们可以通过为视图设置一个触摸监听器(OnTouchListener)来监听用户的触摸事件。当用户触摸视图时,系统会调用onTouch()方法来处理这些事件。
在Android开发中,用户界面(UI)通常在主线程上运行,而OpenGL的渲染则在GLSurfaceView中,这通常在另一个独立的线程上进行。因此,为了在这两个线程之间安全地传递信息,我们需要采用线程安全的通信方式。我们可以通过queueEvent()方法来实现OpenGL线程的调用分发。对于触摸事件的实际处理将在Render的onTouchEvent中实现。
在Android中,触摸事件是在视图的坐标空间内发生的。视图的坐标系统定义为:左上角对应坐标(0, 0),右下角的坐标则等于视图的宽度和高度。例如,如果一个视图的尺寸是480像素宽和800像素高,那么它的右下角坐标就是(480, 800)。
为了在着色器中使用这些坐标,我们需要将触摸事件的坐标转换为归一化设备坐标(NDC),这通常涉及到将y轴方向反转,并将坐标值缩放到[-1, 1]的范围内。这一转换过程是必需的,因为着色器通常使用NDC来处理坐标。
接下来我们看看Renderer的onTouchEvent函数:
fun onTouchEvent(event: MotionEvent){
var x = event.x
var y = event.y
if(event.action == MotionEvent.ACTION_DOWN){
handTouchPress(x,y)
}else{
handleTouchDrag(x,y)
}
}在处理Android触控事件时,我们需要区分事件的类型,因为按压和拖拽事件需要不同的处理方式。按压事件可以通过检查MotionEvent.ACTION_DOWN标志来识别,而拖拽事件则通过MotionEvent.ACTION_MOVE标志来识别。
这里我们先暂且为handleTouchPress()和handleTouchDrag()加入桩代码,之后我们将一步一步完善它们。
private fun handleTouchDrag(x:Float, y:Float ){
}
private fun handTouchPress(x:Float,y:Float){
}1.增加相交测试
我们已经在归一化设备坐标里得到了屏幕的被触碰的区域,就需要决定这个被触碰的区域是否涵盖圆柱体。所以我们需要执行相交测试,这是开发三维游戏和应用时一个非常重要的操作。以下是我们需要做的:
-
1.首先,我们要把二维屏幕坐标转换到三维空间,并看看我们触碰到了什么。要做到这点,我们要把被触碰的点投射到一条射线上,这条射线从我们的视点跨越那个三维场景。
-
2.然后,我们需要检查看看这条射线是否与圆柱体相交。为了使事情简单些,我们假定那个圆柱体实际上是一个差不多同样大小的包围球,然后测试那个球。
让我们以创建两个新的成员变量作为开始:
var blueCylinderPressed = false
lateinit var blueCylinderPosition:Point我们要用blueCylinderPressed跟踪圆柱体当前是否被按到了。我们也把圆柱体的位置存储在blueCylinderPosition,它需要被初始化为一个默认值,因此给onSurfaceCreated()添加如下代码:
blueCylinderPosition = Point(0f,blueCylinder.height/2f,0.4f)接下来按照如下代码更新handTouchPress函数:
private fun handTouchPress(x:Float,y:Float){
val ray: Ray = convertNormalized2DPointToRay(x, y)
val blueCylinderBoundingSphere = Sphere(Point(blueCylinderPosition.x, blueCylinderPosition.y, blueCylinderPosition.z),
blueCylinder.height / 2f)
blueCylinderPressed = Geometry.intersects(blueCylinderBoundingSphere,ray)
}要计算被触碰的点是否与圆柱体相交,我们首先要把被触控的点投射到一条射线上,用一个包围球封装圆柱体,然后测试一下看看那条射线是否与球相交。
我们清楚地触碰了圆柱体。然而,被触碰的区域是在二维空间中,而木槌是在三维空间中。我们怎么测试被触碰的点是否与圆柱体相交呢?
要测试这个,我们首先要把那个二维的点转换为两个三维的点:一个在三维视椎体的近端,另一个在三维视椎体的远端(如果"视椎体"(frustum)这个单词让你一头雾水,现在也是时候回前面篇节,花些时间复习一下)。然后,我们在这两个点之间画一条直线来创建一条射线。
2.二维点扩展成三维直线
通常,当我们把一个三维场景投递到二维屏幕的时候,我们使用透视投影和透视除法把顶点坐标变换为归一化设备坐标。
现在我们想按相反方向变换:我们有被触碰点的归一化设备坐标,我们要计算出在三维世界里那个被触碰的点与哪里相对应。为了把被触碰的点转换为一个三维射线,实质上我们需要取消透视投影和透视除法。
我们当前有被触碰点的x和y坐标,但我们还不知道它应该在多远或多近的地方。要解决这个模糊性,我们把被触碰的点映射到三维空间的一条直线:直线的近端映射到我们在投影矩阵中定义的视椎体的近平面,直线的远端映射到视椎体的远平面。
要实现这个转换,我们需要一个反转的矩阵,它会取消视图矩阵和投影矩阵的效果。让我们给矩阵定义的列表添加如下定义:
private var invertedViewProjectionMatrix = FloatArray(16)在onDrawFrame()里,在调用multiplyMM()之后加入如下一行代码:
Matrix.invertM(invertedViewProjectionMatrix,0, viewProjectionMatrix,0)这个调用会创建一个反转的矩阵,我们可以用它把那个二维被触碰的点转换为两个三维坐标。如果场景可以移来移去,它就会影响场景的哪一部分在手指下面,因此我们也把视图矩阵考虑在内。我们通过反转合并后的视图和投影矩阵实现这些。
反转透视投影和透视除法
我们首先定义一个convertNormalized2DPointToRay函数,并通过以下代码开始:
private fun convertNormalized2DPointToRay(x:Float , y:Float):Ray
{
var nearPointNdc = floatArrayOf( x, y, -1f, 1f)
var farPointNdc = floatArrayOf( x, y, 1f, 1f)
var nearPointWorld = FloatArray(4)
var farPointWorld = FloatArray(4)
Matrix.multiplyMV(nearPointWorld, 0, invertedViewProjectionMatrix, 0, nearPointNdc, 0)
Matrix.multiplyMV(farPointWorld, 0, invertedViewProjectionMatrix, 0, farPointNdc, 0)为了把被触碰的点映射到一条射线,我们在归一化设备坐标里设置了两个点:其中一个点是z值为-1的点,而另一个点是z值为+1的点。我们分别把这两个点存储在nearPointNdc和farPointNdc。因为我们不知道w分量应该被设为多大,暂且把它们的w分量设为1。接下来,我们把每个点都与invertedViewProjectionMatrix相乘,得到世界空间中的坐标。
我们也需要撤销透视除法的影响。反转的视图投影矩阵有一个有趣的属性:把顶点和反转的视图投影矩阵相乘以后,nearPointWorld和farPointWorld实际上就含有了反转的w值。这是因为,通常情况下,投影矩阵的主要意义就是创建不同的w值,以便透视除法可以施加它的魔法;因此,如果我们使用一个反转的投影矩阵,我们就会得到一个反转的w。我们所需要做的就是把x、y和z除以这些反转的w,这样就撤销了透视除法的影响。
让我们继续定义convertNormalized2DPointToRay():
divideByW(nearPointWorld)
divideByW(farPointWorld)divideByW的定义如下:
private fun divideByW(vector: FloatArray) {
vector[0] /= vector[3]
vector[1] /= vector[3]
vector[2] /= vector[3]
}定义一条射线
我们现在已经成功地把一个被触碰的点转换为世界空间中的两个点了。我们现在可以用这两个点定义一个跨越那个三维场景的射线了。让我们完成convertNormalized2DPointToRay():
val nearPointRay = Point(nearPointWorld[0], nearPointWorld[1], nearPointWorld[2])
val farPointRay = Point(farPointWorld[0], farPointWorld[1], farPointWorld[2])
return Ray(nearPointRay, Geometry.vectorBetween(nearPointRay, farPointRay))我们同样需要增加Ray类的定义。让我们给Geometry类加入如下代码:
class Ray {
var point:Point
var vector:Vector
constructor(point:Point , vector:Vector )
{
this.point = point;
this.vector = vector;
}
}一条射线包含一个起点和一个表示射线方向的向量。为了得到这个向量,我们调用vectorBetween()创建了一个从近点指向远点的向量。
让我们在Geometry类中为Vector类加入一个基本的定义:
class Vector(var x: Float, var y: Float,var z: Float) {
fun length():Float = sqrt(x*x+y*y+z*z)
fun crossProduct(other:Vector):Vector = Vector(
(y*other.z) - (z*other.y),
(z*other.x) - (x*other.z),
(x*other.y) - (y*other.x)
)
fun dotProduct(other:Vector):Float = x * other.x + y * other.y + z * other.z
fun scale(f:Float):Vector = Vector(x * f, y * f, z * f)
}这里的length、crossProduct、dotProduct和scale函数我们后面会讲到,暂且知道添加了这些即可。
然后我们还需要定义一个vectorBetween:
fun vectorBetween(from: Point, to: Point): Vector {
return Vector(to.x - from.x, to.y - from.y, to.z - from.z)
}我们现在已经完成了第一部分:把一个被触碰的点转换为一条三维射线。现在我们需要加入相交测试了。
3.执行相交测试
我们稍早前提到过,如果我们假定圆柱体是一个球体,相交测试就会相当容易。实际上,
如果我们回过头去看看handleTouchPress(),我们定义了一个与圆柱体大小相当的包围球:
val blueCylinderBoundingSphere = Sphere(Point(blueCylinderPosition.x, blueCylinderPosition.y, blueCylinderPosition.z),
blueCylinder.height / 2f)我们还没有定义Sphere类,让我们继续在Geometry添加如下代码:
class Sphere(var center:Point, var radius:Float)再看一眼 handleTouchPress(),我们还需要加入相交测试:
blueCylinderPressed = Geometry.intersects(blueCylinderBoundingSphere,ray)使用三角形计算距离
在我们为此编写代码之前,让我们把这个相交测试可视化,因为这会使得它更容易理解:
为了执行这个测试,我们需要遵循以下步骤:
-
我们需要计算出球体与射线之间的距离。要得到这个距离,我们首先定义射线上的两个点:起始点和结束点,结束点是由起始点与射线的向量相加而得。接下来,在这两个点与球体的中心点之间创建一个虚拟三角形,最后,通过计算三角形的高就得到了这个距离。
-
接下来我们比较那个距离和球体的半径。如果那个距离比半径小,那么射线就与球体相交。
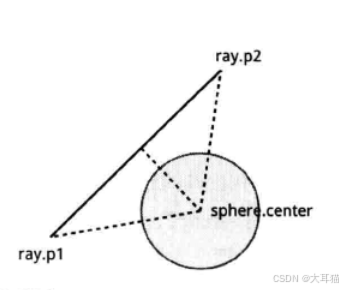
让我们开始编写代码吧。给Geometry类加入如下方法:
fun intersects(sphere: Sphere, ray: Ray): Boolean {
return distanceBetween(sphere.center, ray) < sphere.radius
}这个方法会决定球心与射线的距离,并检查那个距离是否小于球体半径。如果是,那球体就与射线相交。
用向量计算距离
继续并为distanceBetween()写出如下代码:
fun distanceBetween(point: Point, ray: Ray): Float {
var p1ToPoint = vectorBetween(ray.point, point)
var p2ToPoint = vectorBetween(ray.point.translate(ray.vector), point);
val area0fTriangleTimesTwo: Float = p1ToPoint.crossProduct(p2ToPoint).length()
val length0fBase: Float = ray.vector.length()
return area0fTriangleTimesTwo / length0fBase
}这个方法看起来有点复杂,但是它只是执行我们刚刚提到过的三角形方法而已。
我们首先定义了两个向量:一个是从射线的第一个点到球心,另一个是从射线的第二个点到球心。这两个向量一起定义了一个三角形。
要得到这个三角形的面积,我们首先需要计算这两个向量的交叉乘积(cross product)。计算这个交叉乘积会得到第三个向量,它垂直于前两个向量,但是对我们更重要的特性是,这个向量的长度恰好是前两个向量定义的三角形的面积的两倍。
一旦得到了三角形的面积,就可以使用三角形公式计算三角形的高了,这个高就是射线与球体中心点的距离。这个高度等于(area*2)/lengthOfBase。我们在areaOfTriangleTimesTwo中存储了area*2,并利用ray.vector的长度计算三角形底边的长度。要计算三角形的高度,我们只需要把一个除以另外一个。一旦我们有了这个距离,就可以把它与球体的半径作比较了,看看这个射线是否与球体相交。
要是这行得通,我们需要给Point类加入一个新的方法:
fun translate(vector:Vector):Point{
return Point(x+vector.x,y+vector.y,z+vector.z)
}这里还是使用了我们上面在Vector中定义的两个方法,第一个方法-length()利用勾股定理返回向量的长度。第二个方法-crossProduct计算两个向量的交叉乘积。
通过拖动移动圆柱体
既然可以测试圆柱体是否被触碰了,我们将努力解决剩下一部分工作:当我们来回拖动圆柱体的时候,它要去哪里?我们可以用这种方式考虑事情:圆柱体平放在桌子上面,当我们来回移动手指的时候,圆柱体应该随着手指移动并继续平放在桌子上。我们可以通过执行射线-平面(ray-plane)相交测试计算出它的正确位置。
让我们完成handleTouchDrag()的定义:
private fun handleTouchDrag(x:Float, y:Float ){
if(!blueCylinderPressed) return
val ray = convertNormalized2DPointToRay(x, y)
var plane = Plane(Point(0f,0f,0f), Vector(0f,1f,0f))
val touchedPoint: Point = Geometry.intersectionPoint(ray, plane)
blueCylinderPosition = Point(touchedPoint.x, blueCylinder.height / 2f, touchedPoint.z)
}只有当我们开始就用手指按住那个圆柱体时,我们才想要拖动它,因此,首先检查blueCylinderPressed是否为true,如果是,那我们就做射线转换,它与我们在handleTouchPress()中的转换是一样的。一旦我们有了表示被触碰点的射线,我们就要找出这条射线与表示场景区域的平面在哪里相交了,然后,把圆柱体移动到那个点。
在Geometry类中为Plane类加入代码:
class Plane(var point:Point,var normal:Vector)平面的定义非常简单:它包含一个法向向量(normal vector)和平面上的一个点;法向向量仅仅是一个垂直于那个平面的一个向量。平面也有其他可能的定义,但这个是我们要使用的定义。
在下图中,我们可以看到平面的一个例子,它位于(0,0,0),有一个法向向量(0,1,0):
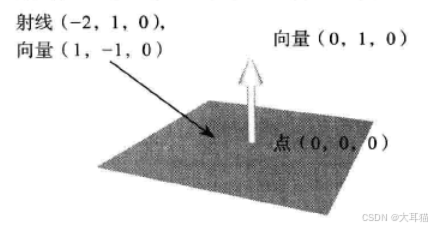
这里还画了一条射线,位于(-2,1,0),且有一个向量(1,-1,0)。我们要使用这个平面和射线解释相交测试。让我们加入如下代码计算那个交点:
fun intersectionPoint(ray:Ray, plane:Plane ):Point{
var rayToPlaneVector = vectorBetween(ray.point, plane.point)
var scaleFactor= rayToPlaneVector.dotProduct(plane.normal)/ ray.vector.dotProduct(plane.normal)
var intersectionPoint= ray.point.translate(ray.vector.scale(scaleFactor));
return intersectionPoint;
}要计算这个交点,我们需要计算出射线的向量要缩放多少才能刚好与平面相接触;这就是缩放因子(scaling factor)。接下来我们用这个被缩放的向量平移射线的点来找出这个相交点。
要计算这个缩放因子,我们首先创建一个向量,它在射线的起点和平面上的一个点之间。然后计算那个向量与平面的法向向量之间的点积(dot product)。
这两个向量的点积与它们之间的余弦直接相关(尽管通常不相等)。举个例子,如果有两个平行的向量,(1,0,0)和(1,0,0),那它们之间的角度就是0度,这个角的余弦就是1。如果有两个相互垂直的向量,(1,0,0)和(0,0,1),那它们之间的角度就是90度,这个角的余弦就是0。
为了计算这个缩放量,我们可以用射线到平面(ray-to-plane)的向量与平面法向向量之间的点积除以射线向量与平面法向向量的点积。这就得到了我们需要的缩放因子。
当射线与平面平行时,一个特殊的情况就会发生:在这种情况下,射线与平面是不可能有交点的。射线会与平面的法向向量相垂直,它们之间的点积将为0,当我们想计算缩放因子的时候,会得到一个除以0的除法。最终,我们会得到一个"相交点",所有分量都是浮点数NaN,它是"不是一个数字"(Not a Number)的缩写。
如果你不理解所有的细节,也不用担心。重要的是它可以工作;对于数学上的好奇,你可以在百度那里学到更多内容。
我们这里也用到了Vector.dotProduct和scale函数,第一个方法-dotProduct()计算两个向量之间的点积。第二个方法-scale()用那个缩放量均匀地缩放向量的每个分量。
为了使 handleTouchDrag()工作,我们已经加入了所有需要的代码。只剩下一个部分:我们需要回到Renderer,当绘制那个蓝色的圆柱体时,实际使用这个新的点。让我们更新 onDrawFrame(),并把第二个 positionObjectInScene()调用更新为如下代码:
positionObjectInScene(blueCylinderPosition.x,blueCylinderPosition.y,blueCylinderPosition.z)运行一下程序;现在你应该能在屏幕上来回拖动那个圆柱体了,它会随着你的指尖移动!
增加碰撞检测
首先在Render中增加如下边界定义:
var leftBound = -0.5f
var rightBound = 0.5f
var farBound = -0.8f
var nearBound = 0.8f这些定义与桌子的四边相对应。现在我们可以更新handleTouchDrag(),并用下面的代码替换blueCylinderPosition的赋值:
blueCylinderPosition = Point(
clamp(touchedPoint.x,leftBound+blueCylinder.radius,rightBound-blueCylinder.radius),
blueCylinder.height / 2f,
clamp(touchedPoint.z,0f+blueCylinder.radius,nearBound-blueCylinder.radius)
)如果我们回顾一下handleTouchDrag(),就会记得touchedPoint代表一个相交点,它是我们触碰屏幕的点与桌子所在平面的相交点。圆柱体就想移动到这个点上。
要保持圆柱体不超出桌子的边界,我们把touchedPoint限定在桌子的边界内。圆柱体不能跨过桌子的任何一条边。通过使用0f,而不是farbound,我们也把桌子的分隔线考虑进来,这样就不会跨到另一边了,并且我们还把圆柱体的半径计算在内了,这样圆柱体的边就不能越过我们所设置的边界的边了。
我们还需要为clamp()加入定义:
private fun clamp(value:Float,min:Float,max:Float):Float{
return max.coerceAtMost(min.coerceAtLeast(value))
}继续并再次运行这个应用。你现在应该发现那个蓝色圆柱体拒绝移到边界外了。
增加速度和方向
接下来我们将实现两个圆柱体的相撞功能,我们上面添加的的圆柱体后面会被成为蓝色圆柱体,在此我们将继续添加一个红色的圆柱体。
lateinit var redCylinder:Cylinder
redCylinder = Cylinder(0.08f,0.04f,32)我们可以添加一些代码来用蓝色圆柱体撞击红色圆柱体,要知道红色圆柱体应该如何作出反应,我们需要回答两个问题:
-
红色圆柱体要移动多快?
-
红色圆柱体要向那个方向移动?
要回答这两个问题,我们需要随着时间变化持续跟踪红色圆柱体是如何移动的。我们要做的第一件事就是给Renderer加入一个新的成员变量previousBlueMalletPosition:
lateinit var previousBlueCylinderPosition:Point我们要给它赋一个值,在给blueCylinderPosition赋值之前,在handleTouchDrag()中加入如下代码:
previousBlueCylinderPosition = blueCylinderPosition下一步是为红色圆柱体存储它的位置、速度和方向。为Renderer类加人如下成员变量:
lateinit var redCylinderPosition:Point
lateinit var redCylinderVector:Vector我们将使用向量存储红色圆柱体的速度和方向。我们需要初始化这些变量,因此让给onSurfaceCreated()加入如下代码:
redCylinderPosition = Point(0f,redCylinder.height/2f,0f)
redCylinderVector = Vector(0f,0f,0f)我们现在可以在handleTouchDrag()结尾处加入如下的碰撞检测代码,要确保这段代码被放在语句"if(!blueCylinderPressed) return;"之后:
var distance = Geometry.vectorBetween(blueCylinderPosition,redCylinderPosition).length()
if(distance < (redCylinder.radius + blueCylinder.radius)){
redCylinderVector = Geometry.vectorBetween(previousBlueCylinderPosition,blueCylinderPosition)
}这段代码首先检查蓝色圆柱体和红色圆柱体之间的距离,然后,它会看那个距离是否小于它们的半径之和。如果是,那蓝色圆柱体就击中了红色圆柱体,并且我们用前一个蓝色圆柱体的位置和当前圆柱体的位置给红色圆柱体创建了一个方向向量。蓝色圆柱体移动得越快,那个向量就会越大,红色圆柱体也会移动得越快。
我们需要更新onDrawFrame(),以便红色圆柱体可以在每一帧上移动。让我们在onDrawFrame()的开始处加入如下代码:
redCylinderPosition = redCylinderPosition.translate(redCylinderVector)作为最后一步,在绘制红色圆柱体之前,也需要更新 positionObjectInScene(),如下代码所示:
positionObjectInScene(redCylinderPosition.x,redCylinderPosition.y,redCylinderPosition.z)
colorProgram.setUniforms(modelViewProjectionMatrix,1f,0f,0f)
redCylinder.bindData(colorProgram)
redCylinder.draw()
redCylinderVector = redCylinderVector.scale(0.99f)加入边界反射
我们现在有了另外一个问题:红色圆柱体可以移动,但是它只是一直不停地向前移动。
为了修复这个问题,我们也不得不给红色圆柱体增加边界检查,并且,无论何时当它撞到桌子边缘,都要把它从桌子边缘弹开。
在onDrawFrame()中,我们可以在redCylinderPosition.translate()调用之后加入如下代码:
checkRedCylinderBound()让我们继续定义checkRedCylinderBound函数:
private fun checkRedCylinderBound(){
if(redCylinderPosition.x < leftBound + redCylinder.radius || redCylinderPosition.x > rightBound - redCylinder.radius){
redCylinderVector = Vector(-redCylinderVector.x,redCylinderVector.y,redCylinderVector.z)
redCylinderVector = redCylinderVector.scale(0.9f)
}
if(redCylinderPosition.z < farBound + redCylinder.radius || redCylinderPosition.z > nearBound - redCylinder.radius){
redCylinderVector = Vector(redCylinderVector.x,redCylinderVector.y,-redCylinderVector.z)
redCylinderVector = redCylinderVector.scale(0.9f)
}
redCylinderPosition = Point(
clamp(redCylinderPosition.x,leftBound + redCylinder.radius,rightBound - redCylinder.radius),
redCylinderPosition.y,
clamp(redCylinderPosition.z,farBound + redCylinder.radius,nearBound - redCylinder.radius)
)
}我们首先检查红色圆柱体是否向左移动得过远或是向右移动得过远了。如果是,那我们就通过反转那个向量的x分量变换它的方向。
我们接着检查红色圆柱体是否越过了桌子的近边或远边。在这种情况下,我们通过反转那个向量的z分量变换它的方向。不要对z的检查感到困惑,因为负的z值指的是距离,东西离得越远,z值越小。
最后,通过把红色圆柱体限定在桌子的边界内,我们把它放回桌子的范围内了。如果我们再试一下这个程序,冰球现在应该在桌子内来回弹了,而不是飞离它的边界。
增加摩擦
红色圆柱体的移动方式还有一个大问题:它永远不会慢下来!这看起来非常不现实,因此,我们要加入一些模拟阻尼的代码使红色圆柱体渐渐地慢下来。要使红色圆柱体在每一帧中慢下来,在onDrawFrame()中,红色圆柱体相关的代码结尾处加入如下代码:
redCylinderVector = redCylinderVector.scale(0.99f)如果再运行一次这个程序,我们就会看到红色圆柱体慢下来了,并最终停了下来。通过给桌子的反弹加入额外的阻尼,我们可以使这个场景更加真实。一旦落入每次反弹检查的条件体内,加入两遍下面的代码:
redCylinderVector = redCylinderVector.scale(0.9f)现在,当红色圆柱体从桌子边缘弹开时,我们将看到它变得更慢了。
小结
在本篇中,我们探索了多个引人入胜的主题。我们首先掌握了如何通过触摸屏幕来控制一个蓝色的圆柱体运动,随后,我们又学习了如何使一个红色圆柱体在桌面上反弹。在开发过程中,你可能已经遇到了重叠问题,这个问题我们将在后面篇节中讨论解决方案。
虽然有些数学概念可能难以理解,但更重要的是在高层次上理解这些概念,这样我们才能知道如何应用它们。幸运的是,有许多优秀的库可以简化我们的工作,例如Bullet physics和JBox2D。
随着本篇的结束,我们不妨花些时间回顾我们当前所掌握的一切。在整个过程中,我们学习了许多重要概念。我们了解了着色器的工作原理,并通过学习颜色、矩阵和纹理,我们甚至学会了如何构建简单的物体,并能够通过手指与它们互动。请为你已经学到的知识和完成的工作感到自豪,因为这一切都是我们通过直接使用OpenGL在底层实现的。