
摘要
无人机路径规划是确保无人机飞行任务高效执行的重要技术。蝙蝠算法(Bat Algorithm, BA)作为一种智能优化算法,被广泛应用于路径规划中。然而,标准蝙蝠算法存在早熟收敛和局部最优等问题。本文提出了三种不同的改进策略,包括基于差分进化算法的混合蝙蝠算法(DEBA),结合人工势场法的混沌蝙蝠算法(CPFIBA),以提升蝙蝠算法在路径规划中的性能。通过对比实验表明,改进的算法能够有效克服局部最优,提供更短的路径和更优的飞行性能。
理论
1. 蝙蝠算法 (BA)
蝙蝠算法模仿蝙蝠在回声定位中寻找猎物的行为。通过模拟蝙蝠发射的超声波信号以及反射回波的时间差,调整蝙蝠的位置以找到最优解。算法的核心包括频率、脉冲发射率和响度三个参数,这些参数决定了蝙蝠的搜索范围和搜索行为。
2. 差分进化算法 (DEBA)
差分进化算法(DE)是一种经典的进化算法,通过差分变异和交叉操作生成新解,具有强大的全局搜索能力。将其与蝙蝠算法结合可以克服BA容易陷入局部最优的问题。
3. 改进的混沌蝙蝠算法 (CPFIBA)
混沌理论强调系统的非线性和随机性,能够增强全局搜索能力,避免算法陷入局部最优。结合人工势场法的混沌蝙蝠算法通过引入人工势场,建立障碍物的排斥力场,同时使用混沌映射提高算法的多样性和搜索效率。
实验结果
为了验证改进算法的有效性,本文使用了典型的无人机路径规划任务进行仿真实验。
-
收敛曲线 图1展示了不同算法的收敛曲线,其中CPFIBA表现出最快的收敛速度,其次是DEBA,而原始BA的收敛速度最慢。
-
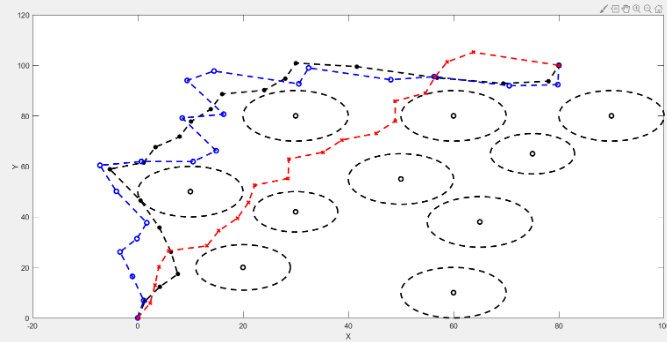
路径规划图 图2展示了无人机路径规划的结果。可以看出,CPFIBA算法规划出的路径较为平滑,并成功避开了所有障碍物,而DEBA次之,BA的路径则表现出较大的波动。
-
3D路径图 图3为3D路径规划图,展示了无人机在不同地形条件下的路径规划结果。从图中可以看出,CPFIBA在复杂环境中的表现优于其他两种算法,能够找到更短、更平滑的路径。
综上所述,改进的混沌蝙蝠算法和差分进化蝙蝠算法在路径规划任务中表现出更优异的性能。


部分代码
% 参数初始化
n = 50; % 蝙蝠种群大小
Max_iter = 100; % 最大迭代次数
A = 0.5; % 响度
r = 0.5; % 脉冲发射率
Qmin = 0; % 最小频率
Qmax = 2; % 最大频率
% 初始种群位置和速度
for i = 1:n
Sol(i,:) = rand(1, 2); % 初始化蝙蝠位置
v(i,:) = zeros(1, 2); % 初始化蝙蝠速度
end
% 差分进化参数
F = 0.5; % 差分进化的缩放因子
Cr = 0.9; % 交叉概率
% 主循环
for t = 1:Max_iter
for i = 1:n
Q = Qmin + (Qmax - Qmin) * rand; % 更新频率
v(i,:) = v(i,:) + (Sol(i,:) - Best) * Q; % 更新速度
S(i,:) = Sol(i,:) + v(i,:); % 更新位置
% 差分进化操作
if rand < Cr
idx = randperm(n, 3);
mutant = Sol(idx(1),:) + F * (Sol(idx(2),:) - Sol(idx(3),:));
if rand < r
S(i,:) = mutant;
end
end
% 更新适应度
fitness = objective_function(S(i,:));
if fitness < best_fitness
Best = S(i,:);
best_fitness = fitness;
end
end
end
% 输出最优路径
disp(['最优路径: ', num2str(Best)]);参考文献
❝
Yang, X.-S. "A new metaheuristic bat-inspired algorithm." In: Nature Inspired Cooperative Strategies for Optimization (NISCO 2010). Springer, 2010, pp. 65-74.
Storn, R., and Price, K. "Differential evolution -- a simple and efficient heuristic for global optimization over continuous spaces." Journal of Global Optimization, 11(4), 1997, pp. 341-359.
Olariu, A., and Macovei, A. "Modified bat algorithm for solving the multi-objective path planning problem." In: IEEE Congress on Evolutionary Computation (CEC), 2016, pp. 2532-2539.
Kennedy, J., and Eberhart, R. "Particle swarm optimization." In: Proceedings of ICNN'95 -- International Conference on Neural Networks, 1995, vol. 4, pp. 1942-1948.
(文章内容仅供参考,具体效果以图片为准)